Secant, Tangent, or External Line to a Hyperbola
A line $$ a'x+b'y+c=0 $$ and a hyperbola $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 $$ can intersect in three ways: secant, tangent, or external.
- If they intersect at two points, they are secant.
- If they intersect at one point, they can either be tangent or the line is parallel to an asymptote.
- If they do not intersect, they are external.
Therefore, having only one point of intersection does not necessarily mean the line is tangent.
To determine the position of the line relative to the hyperbola, we need to solve the system of equations:
$$ \begin{cases} \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 \\ \\ a'x+b'y+c=0 \end{cases} $$
Then, we analyze the resolvent equation.
- If the resolvent equation is quadratic:
- $ \Delta > 0 $
If the discriminant is greater than zero, there are two real solutions, and the line intersects the hyperbola at two distinct points.
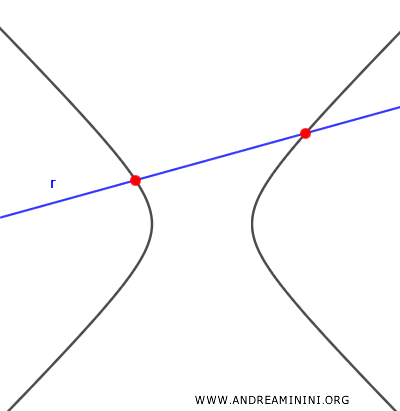
- $ \Delta = 0 $
If the discriminant is zero, there is one real solution, and the line is tangent to the hyperbola.
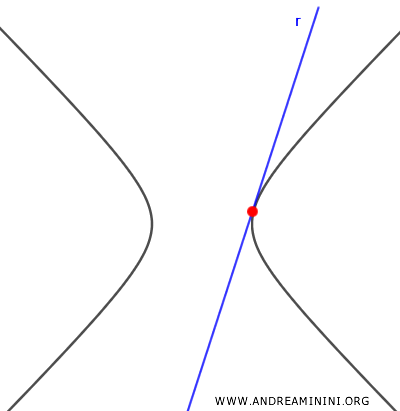
- $ \Delta < 0 $
If the discriminant is negative, there are no real solutions, and the line is external to the hyperbola.
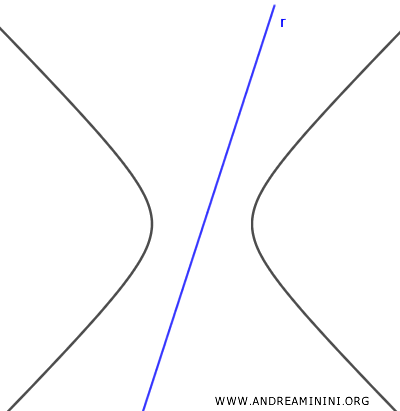
- $ \Delta > 0 $
- If the resolvent equation is linear, the line intersects the hyperbola at one point.
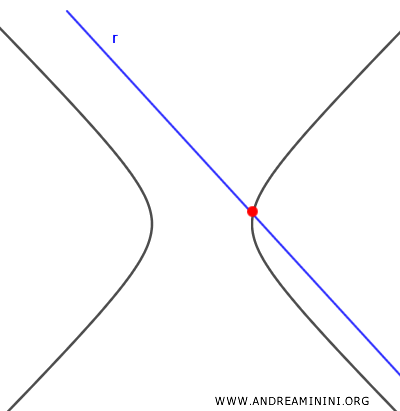
A Practical Example
Consider the hyperbola:
$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$
and the line:
$$ x+y-1=0 $$
We need to determine if they are tangent, secant, or external.
We set up the system of equations:
$$ \begin{cases} \frac{x^2}{4} - \frac{y^2}{3} = 1 \\ \\ x+y-1=0 \end{cases} $$
We isolate y in both equations:
$$ \begin{cases} y^2 = 3 \cdot ( \frac{x^2}{4} - 1 ) \\ \\ y=1-x \end{cases} $$
$$ \begin{cases} y = \sqrt{ \frac{3x^2}{4} - 3 } \\ \\ y=1-x \end{cases} $$
Then, we equate the equations y=y to obtain the resolvent equation:
$$ \sqrt{ \frac{3x^2}{4} - 3 } = 1 - x $$
$$ ( \sqrt{ \frac{3x^2}{4} - 3 } )^2 = ( 1 - x )^2 $$
$$ \frac{3x^2}{4} - 3 = 1 -2x+x^2 $$
$$ \frac{3x^2}{4} - 3 - 1 +2x-x^2 = 0 $$
$$ \frac{3x^2-4x^2}{4} +2x - 4 = 0 $$
$$ -\frac{x^2}{4} +2x -4= 0 $$
The resolvent equation is quadratic, so the line is not parallel to an asymptote of the hyperbola.
We calculate the discriminant of the quadratic equation:
$$ \Delta = b^2 - 4ac $$
Where $ a = - \frac{1}{4} $, $ b=2 $, $ c=-4 $
$$ \Delta = 2^2 - 4 \cdot ( - \frac{1}{4} ) \cdot (-4) $$
$$ \Delta = 4 - 4 $$
$$ \Delta = 0 $$
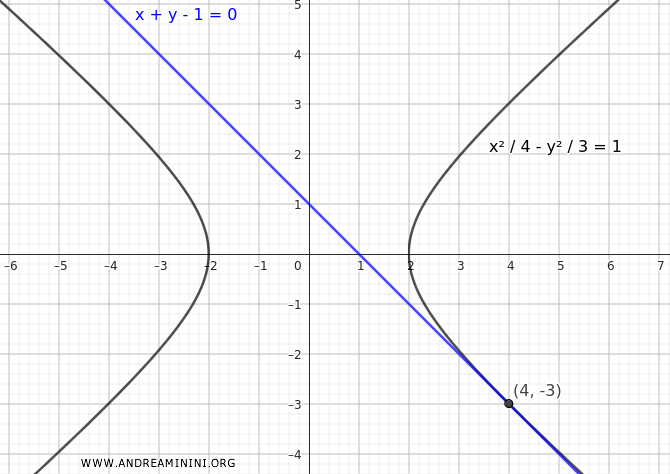
The discriminant is zero, so the line is tangent to the hyperbola.
We calculate the x-coordinate of the tangent point:
$$ x = \frac{-b \pm \Delta}{2a} $$
$$ x = \frac{-2 \pm 0}{2 \cdot (- \frac{1}{4} )} $$
$$ x = \frac{-2}{- \frac{1}{2}} $$
$$ x = \frac{2}{ \frac{1}{2}} $$
$$ x = 2 \cdot \frac{2}{1} $$
$$ x = 4 $$
Once we have the x-component $ x=4 $ of the tangent point, we substitute it into the line equation to get the y-component:
$$ y=1-x $$
$$ y=1-4 $$
$$ y=-3 $$
So, the tangent point is at the coordinates $ (x;y)=(4;-3) $
Example 2
Consider the hyperbola:
$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$
and the line:
$$ y = - \frac{ \sqrt{3} }{2} x+\frac{1}{2} $$
We need to determine if the line is secant, tangent, or external.
Note: By observing the slope of the line $ - \frac{ \sqrt{3} }{2} $, we can already tell that the line is parallel to an asymptote of the hyperbola. The asymptotes of the hyperbola are given by the equation $$ y = \pm \frac{b}{a}x $$ In this case $ a^2=4 $ and $ b^2 = 3 $ , so $ a= 2 $ and $ b= \sqrt{3} $. $$ y = \pm \frac{\sqrt{3}}{2}x $$ Therefore, the slope of the line matches that of an asymptote. From this, we can already deduce that the line intersects the hyperbola at one point. However, for completeness, we will perform all the calculations.
We set up the system of equations:
$$ \begin{cases} \frac{x^2}{4} - \frac{y^2}{3} = 1 \\ \\ y = - \frac{ \sqrt{3} }{2} x+\frac{1}{2} \end{cases} $$
$$ \begin{cases} y^2 = 3 \cdot ( \frac{x^2}{4} - 1 ) \\ \\ y = - \frac{ \sqrt{3} }{2} x+\frac{1}{2} \end{cases} $$
$$ \begin{cases} y = \sqrt{ \frac{3x^2}{4} - 3 } \\ \\ y = - \frac{ \sqrt{3} }{2} x+\frac{1}{2} \end{cases} $$
So, the resolvent equation by equating y=y is:
$$ \sqrt{ \frac{3x^2}{4} - 3 } = - \frac{ \sqrt{3} }{2} x+\frac{1}{2} $$
$$ ( \sqrt{ \frac{3x^2}{4} - 3 } )^2 = ( - \frac{ \sqrt{3} }{2} x+\frac{1}{2} )^2 $$
$$ \frac{3x^2}{4} - 3 = (- \frac{ \sqrt{3} }{2} x )^2 + 2 \cdot (- \frac{ \sqrt{3} }{2} x ) \cdot \frac{1}{2} + ( \frac{1}{2} )^2 $$
$$ \frac{3x^2}{4} - 3 = \frac{ 3 }{4} x^2 - \frac{\sqrt{3} x}{2} + \frac{1}{4} $$
$$ \require{cancel} \cancel{ \frac{3x^2}{4} } - 3 - \cancel{ \frac{ 3 }{4} x^2 } + \frac{\sqrt{3} x}{2} - \frac{1}{4} = 0 $$
$$ \frac{\sqrt{3} x}{2} - 3 - \frac{1}{4} = 0 $$
$$ \frac{\sqrt{3} x}{2} - \frac{12}{4} - \frac{1}{4} = 0 $$
$$ \frac{\sqrt{3} x}{2} - \frac{13}{4} = 0 $$
The resolvent equation is linear, so the line intersects the hyperbola at one point.
This means the line is parallel to an asymptote of the hyperbola.
Now, we find the x-component of the intersection point:
$$ x = \frac{13}{4} \cdot \frac{2}{ \sqrt{3}} $$
$$ x = \frac{13}{2 \sqrt{3} } $$
Note: The asymptotes of the hyperbola are $$ y = \pm \frac{b}{a} x $$ where $ a = 2 $ and $ b = \sqrt{3} $ $$ y = \pm \frac{\sqrt{3}}{2} x $$ As you can see, the slope of an asymptote is equal to the slope of the line $ -\frac{ \sqrt{3} }{2} $
To find the y-component of the intersection point, we substitute $ x = \frac{13}{2 \sqrt{3} } $ into the line equation:
$$ y = - \frac{ \sqrt{3} }{2} x+\frac{1}{2} $$
$$ y = - \frac{ \sqrt{3} }{2} \cdot \frac{13}{2 \sqrt{3} } +\frac{1}{2} $$
$$ y = - \frac{13}{4} +\frac{1}{2} $$
$$ y = \frac{-13+2}{4} $$
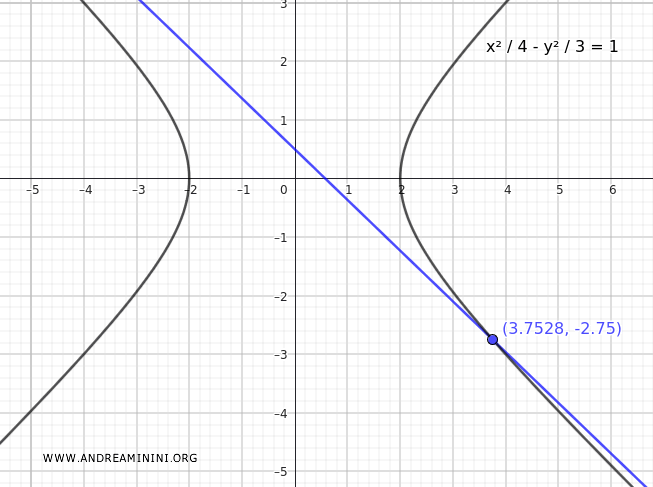
$$ y = -\frac{11}{4} $$
Here is the graph of the line and the hyperbola intersecting at one point:
And so on.
