Tangent line equation involving a point of tangency of hyperbola
The tangent line formula allows us to find the tangent line at a point $P(x_0;y_0)$ on a hyperbola. $$ \frac{xx_0}{a^2} - \frac{yy_0}{b^2} = \pm 1 $$
This formula is derived by substituting into the standard equation of the hyperbola $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 $$ with $ x^2 \rightarrow xx_0 $ and $ y^2 \rightarrow yy_0 $.
It comes from applying the conic section formulas specifically to hyperbolas.
Note: These formulas are useful only for obtaining the equation of the tangent line at a point on the hyperbola. They cannot be used if the point is not on the hyperbola.
A Practical Example
Consider the equation of a hyperbola:
$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$
We want to find the tangent line at the point $P(4;3)$ on the hyperbola.
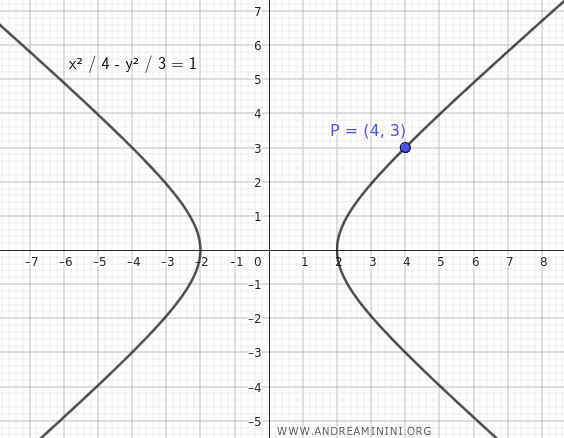
First, we verify if the point $P$ is on the hyperbola by substituting the coordinates $x=4$ and $y=3$ into the hyperbola's equation.
$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$
$$ \frac{4^2}{4} - \frac{3^2}{3} = 1 $$
$$ 4 - 3 = 1 $$
$$ 1 = 1 $$
The equation holds true, which means the point $P(4;3)$ is on the hyperbola.
Once verified, we apply the doubling formula by substituting $ x^2 \rightarrow xx_0 $ and $ y^2 \rightarrow yy_0 $ into the standard equation of the hyperbola.
$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$
$$ \frac{xx_0}{4} - \frac{yy_0}{3} = 1 $$
The coordinates of the point of tangency are $P(4;3)$, so $x_0 = 4$ and $y_0 = 3$.
$$ \frac{x \cdot 4}{4} - \frac{y \cdot 3}{3} = 1 $$
$$ x - y = 1 $$
$$ y = x - 1 $$
Therefore, the tangent line at the point $P(4;3)$ is $y = x - 1$.
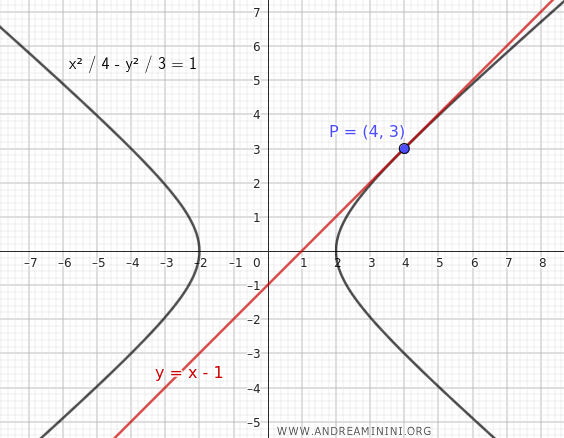
And that's how it's done.
