Finding the Equation of a Hyperbola Given a Vertex and a Tangent Line
To determine the equation of a hyperbola centered at the origin, given a tangent line and a vertex, follow these steps:
- First, identify the transverse axis (the axis along which the foci lie) from the problem data. If the transverse axis is the x-axis, the equation of the hyperbola is $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ If the transverse axis is the y-axis, the equation of the hyperbola is $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
- Set up a system of equations using the standard form of the hyperbola and the equation of the tangent line: $$ \begin{cases} \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 \\ \\ a'x + b'y + c' = 0 \end{cases} $$
- Substitute the known vertex into the system and solve for the missing vertex, keeping in mind that the condition of tangency is met when the discriminant is zero: $ \Delta = 0 $
A Practical Example
Consider a hyperbola centered at the origin that is tangent to the line $ 2x-3y-2=0 $ and has a real vertex at $ A(2;0) $.
Given that the real vertex is at $ A(2;0) $, we deduce that $ a=2 $, and the transverse axis lies along the x-axis. Therefore, the equation of the hyperbola is:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{2^2} - \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{4} - \frac{y^2}{b^2} = 1 $$
Next, we set up a system of equations with the hyperbola's equation and the equation of the line to find the point of tangency:
$$ \begin{cases} 2x-3y - 2 = 0 \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = 1 \end{cases} $$
To confirm the tangency, we substitute the equation of the line into the hyperbola's equation and verify that we obtain a single solution, meaning the line touches the hyperbola at exactly one point.
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = 1 \end{cases} $$
Substituting \(y\) into the hyperbola's equation:
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ \frac{x^2}{4} - \frac{\left( \frac{2x-2}{3} \right)^2}{b^2} = 1 \end{cases} $$
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ \frac{x^2}{4} - \frac{ \frac{4x^2 -8x +4 }{9} }{b^2} = 1 \end{cases} $$
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ \frac{x^2}{4} - \frac{4x^2 -8x +4 }{9} \cdot \frac{1}{b^2} = 1 \end{cases} $$
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ \frac{x^2}{4} - \frac{4x^2 -8x +4 }{9b^2} = 1 \end{cases} $$
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ \frac{9b^2x^2 + 4 \cdot (-4x^2 +8x -4)= }{4 \cdot 9b^2} = 1 \end{cases} $$
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ \frac{9b^2x^2 -16x^2 +32x -16 }{36b^2} = 1 \end{cases} $$
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ 9b^2x^2 -16x^2 +32x -16 = 36b^2 \end{cases} $$
Let's rearrange the terms:
$$ \begin{cases} y = \frac{2x-2}{3} \\ \\ (9b^2 -16)x^2 +32x -16 - 36b^2 = 0 \end{cases} $$
For the line to be tangent to the hyperbola, this quadratic equation must have a single solution, which means the discriminant must be zero.
The discriminant of a quadratic equation \(Ax^2 + Bx + C = 0\) is given by \(B^2 - 4AC\).
$$ \Delta = B^2 - 4AC = 0 $$
In this case, $ A = 9b^2 - 16, \quad B = 32, \quad C = -16 - 36b^2 $.
$$ 32^2 - 4 \cdot (9b^2 -16 ) \cdot (-16 - 36b^2 ) = 0 $$
$$ 1024 - 4 \cdot (9b^2 -16 ) \cdot (-16 - 36b^2 ) = 0 $$
We can simplify by dividing both sides of the equation by 4:
$$ \frac{1}{4} \cdot [ 1024 - 4 \cdot (9b^2 -16 ) \cdot (-16 - 36b^2 ) ] = \frac{1}{4} \cdot 0 $$
$$ 256 - (9b^2 -16 ) \cdot (-16 - 36b^2 ) = 0 $$
$$ 256 - 9b^2 \cdot (-16 - 36b^2 ) + 16 \cdot (-16 - 36b^2 ) = 0 $$
$$ 256 + 144b^2 + 324b^4 - 256 - 576b^2 = 0 $$
$$ 324b^4 - 432b^2 = 0 $$
$$ b^2 ( 324b^2 - 432 ) = 0 $$
The discriminant $ \Delta = 0 $ when $ b^2 = 0 $ or $ b^2 = \frac{432}{324} = \frac{4}{3} $.
We disregard $ b^2 = 0 $ since the semi-axis of the hyperbola cannot be zero, leaving us with $ b^2 = \frac{4}{3} $.
$$ b^2 = \frac{4}{3} $$
$$ \sqrt{b^2} = \sqrt{ \frac{4}{3} } $$
$$ b = 2 \sqrt{ \frac{1}{3} } $$
Now that we know the lengths of the semi-axes, $ a = 2 $ and $ b = 2 \sqrt{ \frac{1}{3} } $, we substitute them into the standard equation of the hyperbola:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{2^2} - \frac{y^2}{( 2 \sqrt{ \frac{1}{3} } )^2} = 1 $$
$$ \frac{x^2}{4} - \frac{y^2}{ \frac{4}{3} } = 1 $$
$$ \frac{x^2}{4} - y^2 \cdot \frac{3}{4} = 1 $$
$$ \frac{x^2}{4} - \frac{3y^2}{4} = 1 $$
We multiply both sides of the equation by 4:
$$ 4 \cdot ( \frac{x^2}{4} - \frac{3y^2}{4} )= 4 $$
$$ x^2 - 3y^2 = 4 $$
This is the equation of the hyperbola centered at the origin, tangent to the line $ 2x-3y-2=0 $, with a real vertex at $ A(2;0) $.
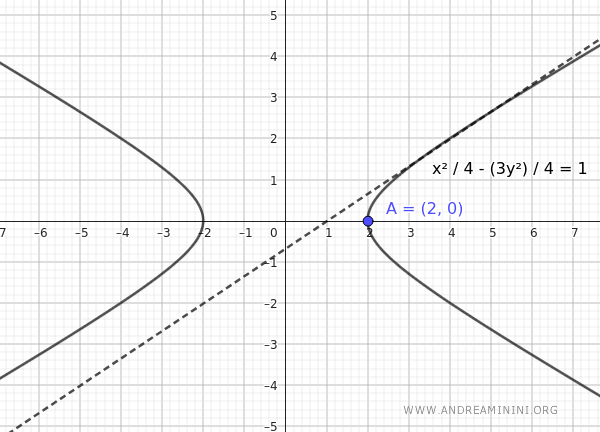
And that's how it's done.
