Finding the Equation of a Hyperbola Given a Point and a Tangent Line

To determine the equation of a hyperbola centered at the origin, given a point on the hyperbola $ P(x,y) $ and the equation of a tangent line, follow these steps:

First, decide whether the transverse axis lies along the x-axis $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ or the y-axis $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$ based on the information provided.
Next, substitute the coordinates of the point $ P(x,y) $ into the standard equation of the hyperbola.
Compare the equation of the given tangent line with the standard form of a tangent line to a hyperbola, $ \frac{x_0x}{a^2} - \frac{y_0y}{b^2} = 1 $, to find the coordinates $ (x_0, y_0) $ of the point of tangency in terms of $ a^2 $ and $ b^2 $. Then, substitute these values into the equation of the tangent line.
Finally, set up a system of equations to solve for $ a^2 $ and $ b^2 $.

A Practical Example

Consider a hyperbola centered at the origin, with its transverse axis along the x-axis. Suppose it passes through the point $ P(-4,3) $ and has a tangent line given by $ x - y = 1 $.

Since the transverse axis is along the x-axis, the standard equation of the hyperbola is:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

Given that the hyperbola passes through the point $P(-4, 3)$, we can substitute $x = -4$ and $y = 3$ into the standard equation to obtain:

$$ \frac{16}{a^2} - \frac{9}{b^2} = 1 \quad \text{(Equation 1)} $$

We also know that the hyperbola has a tangent line defined by the equation $x - y = 1$.

For a hyperbola, the equation of the tangent line at a point $(x_0, y_0)$ is given by:

$$ \frac{x_0x}{a^2} - \frac{y_0y}{b^2} = 1 $$

Comparing this with the given tangent line equation $x - y = 1$, we can identify the following:

$$ \underbrace{ \frac{x_0}{a^2} }_1 x - \underbrace{ \frac{y_0}{b^2} }_1 y= 1 \Leftrightarrow x-y=1 $$

To match the coefficients of $x$ and $y$ in the tangent line equation, we must have:

$$ \frac{x_0}{a^2} = 1 \quad \text{and} \quad -\frac{y_0}{b^2} = -1 $$

This implies:

$$ x_0 = a^2 \quad \text{and} \quad y_0 = b^2 $$

Therefore, the point of tangency $(x_0, y_0)$ on the hyperbola is $(a^2, b^2)$.

Since this line is tangent at this point, we can substitute $x = a^2$ and $y = b^2$ into the tangent line equation $x - y = 1$ to get:

$$ a^2 - b^2 = 1 \quad \text{(Equation 2)} $$

Now we have two equations to solve simultaneously, forming a system with two equations and two unknowns:

$$ \begin{cases} \frac{16}{a^2} - \frac{9}{b^2} = 1 \\ \\ a^2 - b^2 = 1 \end{cases} $$

Let's solve for $ a^2 $ from the second equation:

$$ a^2 = b^2 + 1 $$

Next, substitute $ a^2 = b^2 +1 $ into the first equation:

$$ \frac{16}{b^2 + 1} - \frac{9}{b^2} = 1 $$

$$ \frac{16b^2 - 9(b^2+1)}{b^2(b^2 + 1)} = 1 $$

To solve the first equation, multiply both sides by $b^2(b^2 + 1)$:

$$ 16b^2 - 9(b^2 + 1) = b^4 + b^2 $$

Expanding and rearranging the terms gives:

$$ 16b^2 - 9b^2 - 9 = b^4 + b^2 $$

$$ 7b^2 - 9 = b^4 + b^2 $$

$$ b^4 - 6b^2 + 9 = 0 $$

Substituting $u = b^2$, the equation $ b^4 - 6b^2 + 9 = 0 $ becomes:

$$ u^2 - 6u + 9 = 0 $$

This quadratic equation factors as:

$$ (u - 3)^2 = 0 $$

So, $u = 3$, which means $b^2 = 3$.

Now we can solve for $ a^2 $:

$$ \begin{cases} b^2=3 \\ \\ a^2 = b^2 + 1 \end{cases} $$

Substituting $b^2 = 3$ into $a^2 = b^2 + 1$, we find:

$$ a^2 = 4 $$

Thus, with $ a^2 = 4 $ and $ b^2 = 3 $, the standard equation of the hyperbola is:

$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$

This is the equation of the hyperbola that passes through the point $(-4, 3)$ and has a tangent line given by $x - y = 1$.

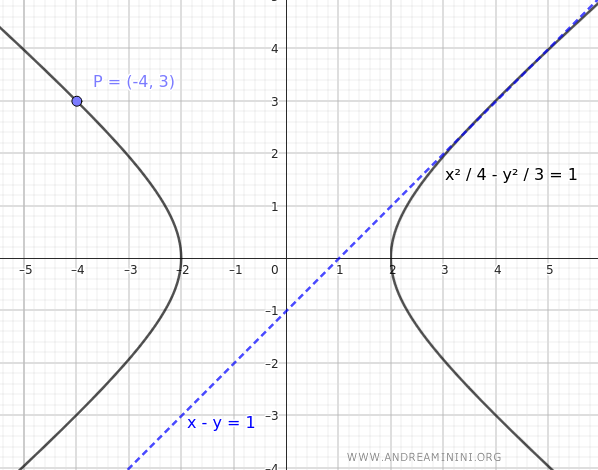
hyperbola graph

And that’s how it’s done.