Equation of the Hyperbola
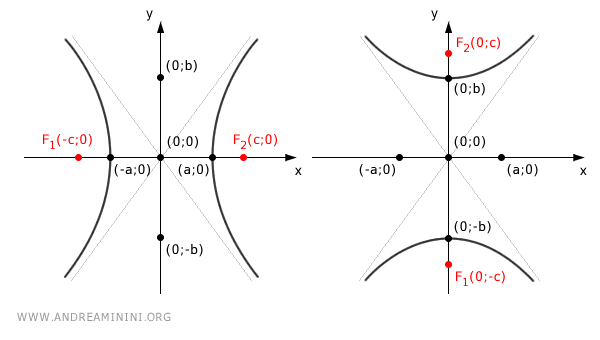
The standard equation of a hyperbola centered at the origin depends on whether the foci are on the x-axis or the y-axis.
- If the foci are on the x-axis, the equation of the hyperbola is $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
- If the foci are on the y-axis, the equation of the hyperbola is $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
Here, \(a\) is the distance from the center \(O\) of the hyperbola to the vertices along the x-axis, while \(b\) is the distance along the y-axis, which determines the shape of the hyperbola.
In both cases, the hyperbola appears as an open curve, symmetric with respect to the x-axis, the y-axis, and the origin, consisting of two branches that are symmetric about these axes.
The center of the hyperbola \((0, 0)\) in standard form is the point of symmetry from which two lines called asymptotes pass, which the hyperbola approaches but never reaches.
The equations of the hyperbola's asymptotes are:
$$ y = \pm \frac{b}{a} x $$
The asymptotes form an angle with the axes and represent the directions toward which the branches of the hyperbola extend infinitely.
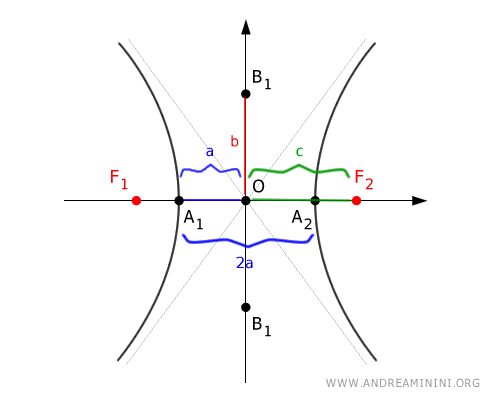
The hyperbola consists of two branches that extend infinitely, each approaching its asymptote.
The foci are two fixed points inside the hyperbola along the x-axis or the y-axis, where the absolute difference of the distances from any point \(P(x;y)\) on the hyperbola is constant and equal to \(2a\).
$$ | \overline{PF_1} - \overline{PF_2} | = 2a $$
Note: If the hyperbola has its foci on the y-axis, the relationship is $$ | \overline{PF_1} - \overline{PF_2} | = 2b $$
The coordinates of the foci are:
- If the foci are on the x-axis: $$ F_1(-c;0) $$ $$ F_2(c;0) $$
- If the foci are on the y-axis: $$ F_1(0;-c) $$ $$ F_2(0;c) $$
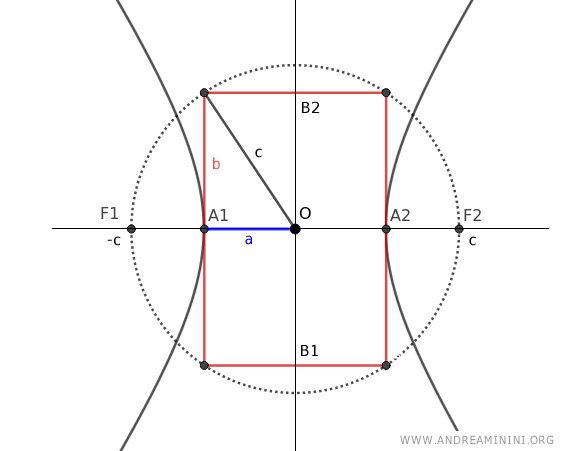
Here, \(c\) is the distance from the center to each focus, while \(a\) and \(b\) are the distances from the center to the vertices, following the relationship:
$$ c = \sqrt{a^2+b^2} $$
Explanation: Draw a circle centered at point O of the hyperbola with radius "c" and a rectangle with sides 2a and 2b centered on the hyperbola's center. Then construct a right triangle with "c" as the hypotenuse and "a" and "b" as the legs. By the Pythagorean theorem, \(c^2 = a^2 + b^2\).
The axis that passes through the foci is called the transverse axis, while the perpendicular axis is called the conjugate axis.
The intersections of the hyperbola with the transverse axis are called vertices and are:
- If the foci are on the x-axis: $$ A_1(-a;0) $$ $$ A_2(a;0) $$
- If the foci are on the y-axis: $$ B_1(0;-b) $$ $$ B_2(0;b) $$
Explanation: To find the vertices' coordinates of a hyperbola with the transverse axis on the x-axis, set \(y = 0\) in the standard hyperbola equation. $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ $$ \frac{x^2}{a^2} - \frac{0^2}{b^2} = 1 $$ $$ \frac{x^2}{a^2} = 1 $$ $$ x^2 = a^2 $$ $$ x = a $$ Similarly, to find the vertices' coordinates in a hyperbola with the transverse axis on the y-axis, set \(x = 0\) in the standard equation. $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$ $$ \frac{0^2}{a^2} - \frac{y^2}{b^2} = -1 $$ $$ - \frac{y^2}{b^2} = -1 $$ $$ - y^2 = - b^2 $$ $$ y^2 = b^2 $$ $$ y = b $$
The vertices on the transverse axis are called the hyperbola's real vertices, while those on the conjugate axis are called imaginary vertices.
The hyperbola's eccentricity is the ratio of the focal distance \(c\) to the length of the transverse axis \(a\) or \(b\).
- If the transverse axis is the x-axis: $$ e = \frac{c}{a} $$
- If the transverse axis is the y-axis: $$ e = \frac{c}{b} $$
Since in a hyperbola \(c > a\) if the transverse axis is the x-axis and \(a > 0\), the eccentricity \(e = \frac{c}{a}\) is always greater than 1 \((e > 1)\).
Note. The same applies if the transverse axis is the y-axis; in this case, \(c > b\) and \(b > 0\), so the eccentricity \(e = \frac{c}{b}\) is always greater than 1 \((e > 1)\).
Every hyperbola has two foci and two directrices that are symmetrical, parallel to each other, and perpendicular to the transverse axis.
If the transverse axis, which contains the foci, coincides with the \(x\)-axis, the directrices are given by:
$$ x = \pm \frac{a^2}{c} $$
On the other hand, if the transverse axis lies along the \(y\)-axis, the directrices are expressed as:
$$ y = \pm \frac{b^2}{c} $$
In general, as with any conic section, for a given point \( P(x;y) \) on the hyperbola, the ratio between the distance \( \overline{PF} \) from the point to the focus and the distance \( \overline{PH} \) from the point to the directrix is constant and corresponds to the hyperbola's eccentricity:
$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$
Below is a practical example illustrating the directrices of a hyperbola.
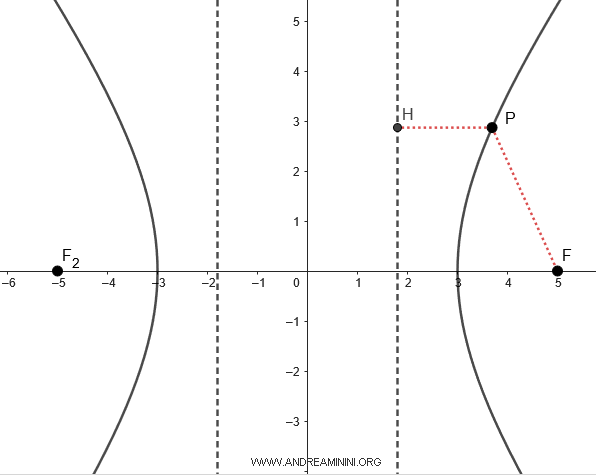
Proof. Consider a hyperbola with its transverse axis along the x-axis: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ The directrices are perpendicular to the x-axis, given by $$ x = k $$ By definition, the ratio of the distance from any point on the hyperbola to the focus and the distance from that same point to the directrix is constant and equal to the eccentricity: $$ \frac{ \overline{PF} }{ \overline{PH} } = e $$ where the eccentricity is defined as \( e=\frac{c}{a} \). $$ \frac{ \overline{PF} }{ \overline{PH} } = \frac{c}{a} $$ Now, let's choose the vertex \( A(a,0) \) of the hyperbola as the point \( P \). The distance \( \overline{PF} = c-a \), while the distance \( \overline{PH} = a-k \). $$ \frac{ c-a }{ a-k } = \frac{c}{a} $$ $$ a \cdot (c-a)= c \cdot (a-k) $$ $$ \require{cancel}\cancel{ac} -a^2 =\cancel{ac} - kc $$ $$ - a^2 \cdot (-1) = - kc \cdot (-1) $$ $$ a^2 = kc $$ $$ k = \frac{a^2}{c} $$ Since the other directrix is parallel and symmetric, the two directrices are located on the x-axis at \( (k;0) \) and \( (-k;0) \). Similarly, if the transverse axis lies along the y-axis, the directrices are \( y = \pm \frac{b^2}{c} \).
Practical Example
Let's consider a hyperbola with \(a = 3\) and \(b = 4\) with the foci on the x-axis.
The equation of the hyperbola is
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{3^2} - \frac{y^2}{4^2} = 1 $$
$$ \frac{x^2}{9} - \frac{y^2}{16} = 1 $$
To better understand, let's plot this hyperbola on a Cartesian plane.
The vertices of the hyperbola are at \((\pm 3, 0)\).
The asymptotes are determined by the equations
$$ y = \pm \frac{4}{3} x $$
By drawing these lines and sketching the branches of the hyperbola approaching the asymptotes, we get the graphical representation of the hyperbola.
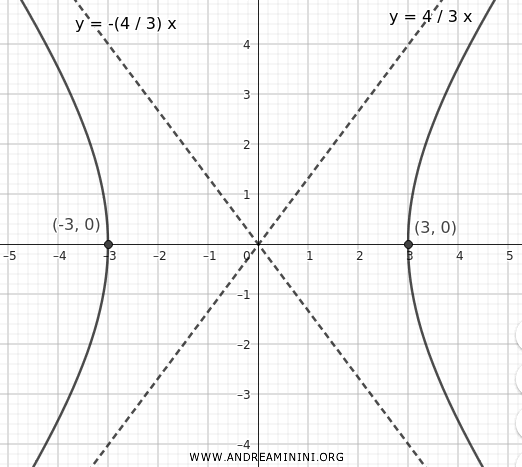
The foci are on the x-axis, so their coordinates are
$$ F_1(-c;0) $$
$$ F_1(c;0) $$
Where \(c^2 = a^2 + b^2\)
$$ c^2 = a^2 + b^2 $$
$$ \sqrt{c^2} = \sqrt{a^2 + b^2} $$
$$ c = \sqrt{a^2 + b^2} $$
Knowing that \(a^ 2 = 9\) and \(b^2 = 16\)
$$ c = \sqrt{9 + 16} $$
$$ c = \sqrt{25} $$
$$ c = 5 $$
So, the foci are at the coordinates:
$$ F_1(-5;0) $$
$$ F_1(5;0) $$
Here's the graphical representation:
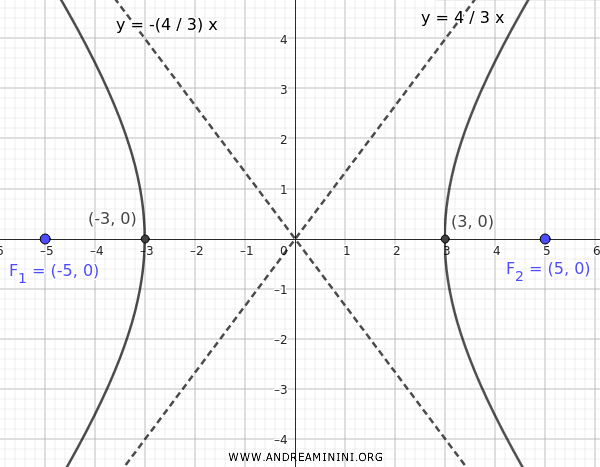
In this case, the transverse axis, which contains the foci, coincides with the x-axis.
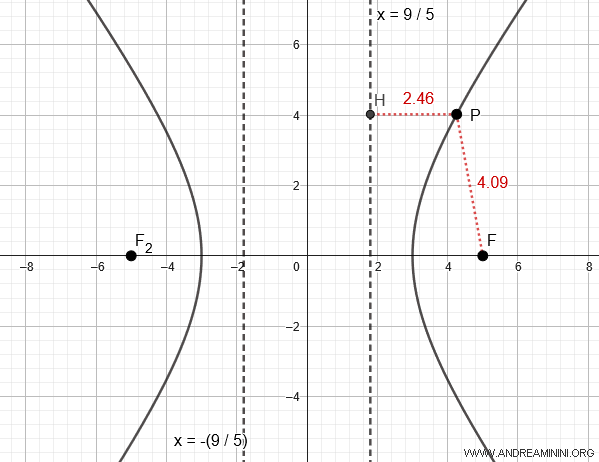
Therefore, the directrices are expressed as:
$$ x = \pm \frac{a^2}{c} $$
Where \( a=3 \) and \( c=5 \).
$$ x = \pm \frac{a^2}{c} = \pm \frac{3^2}{5} = \pm \frac{9}{5} = \pm 1.8 $$
The ratio between the distances \( \overline{PF} \) and \( \overline{PH} \) is constant for any point \( P(x;y) \) on the hyperbola and is equal to the eccentricity \( e \).
$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$
For example, at a specific point \( P \), the distance from the point to the focus is \( \overline{PF} = 4.09 \), while the distance from the same point to the directrix is \( \overline{PH} = 2.46 \).
$$ e = \frac{ \overline{PF} }{ \overline{PH} } = \frac{4.09}{2.46} \approx 1.67 $$
Thus, the eccentricity of the hyperbola is \( e \approx 1.67 \).
This ratio \( e = \frac{ \overline{PF} }{ \overline{PH} } \) holds true for any other point on the hyperbola.
Note. Another way to calculate the eccentricity of the hyperbola is by using the formula $$ e = \frac{c}{a} = \frac{5}{3} \approx 1.67 $$ The final result remains the same.
The Proof
Consider the case where the foci \(F_1(-c;0)\) and \(F_2(c;0)\) are aligned along the x-axis, and the center of the hyperbola is at the origin of the Cartesian axes.
To find the standard equation of the hyperbola, choose any point \(P(x;y)\) on the hyperbola.
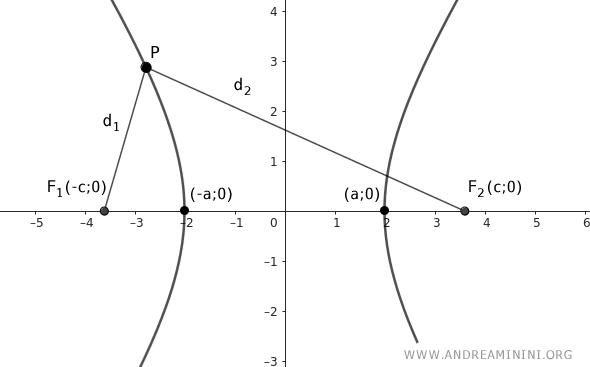
In a hyperbola, the difference in distances from any point to the two foci is equal to \(2a\).
$$ \overline{PF_1} - \overline{PF_2} = 2a $$
Why is the difference in distances equal to 2a? By definition, at any point on a hyperbola, the absolute difference in distances to the foci is constant, and the foci are at a distance "c" from the center.
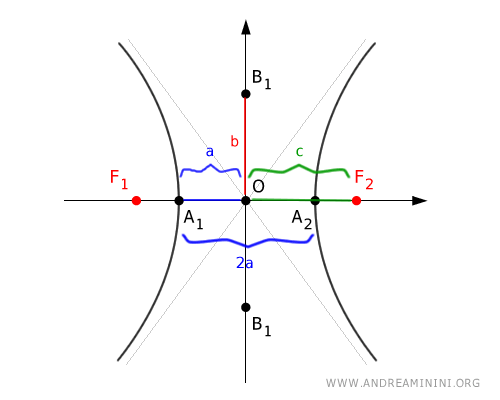
If we consider point \(A_2\), the distance from this point to focus \(F_2\) is \(c-a\), and to focus \(F_1\) it is \(a+c\). $$ \overline{A_2F_2} = c-a $$ $$ \overline{A_2F_1} = a+c $$ Now let's calculate the difference in distances: $$ \overline{A_2F_1} - \overline{A_2F_2} = k $$ $$ (a+c) - (c-a) = k $$ $$ a+c-c+a = k $$ $$ 2a = k $$
Returning to point \(P\)
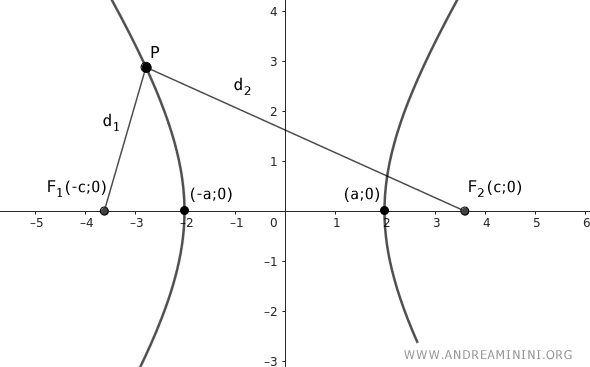
Use the Pythagorean theorem to calculate the distances from point P to the foci.
$$ d_1 = \overline{PF_1} = \sqrt{(x-(-c))^2+(y-0)^2} = \sqrt{(x+c)^2+y^2} $$
$$ d_2 = \overline{PF_2} = \sqrt{(x-c)^2+(y-0)^2} = \sqrt{(x-c)^2+y^2} $$
So, we can also write the difference in distances as follows.
$$ \overline{PF_1} - \overline{PF_2} = 2a $$
$$ \sqrt{(x+c)^2+y^2} - \sqrt{(x-c)^2+y^2} = 2a $$
Move one of the square roots to the right-hand side.
$$ \sqrt{(x+c)^2+y^2} = 2a + \sqrt{(x-c)^2+y^2} $$
Then square both sides of the equation.
$$ (\sqrt{(x+c)^2+y^2})^2 = (2a + \sqrt{(x-c)^2+y^2})^2 $$
$$ (x+c)^2 + y^2 = (2a)^2 + 2 \cdot (2a \sqrt{(x-c)^2+y^2}) + (\sqrt{(x-c)^2+y^2})^2 $$
$$ (x+c)^2 + y^2 = 4a^2 + 4a \sqrt{(x-c)^2+y^2} + (x-c)^2 + y^2 $$
$$ (x+c)^2 = 4a^2 + 4a \sqrt{(x-c)^2+y^2} + (x-c)^2 $$
Now expand the squares of the binomials \((x+c)^2\) and \((x-c)^2\) outside the square root and simplify:
$$ x^2 + 2xc + c^2 = 4a^2 + 4a \sqrt{(x-c)^2+y^2} + x^2 - 2xc + c^2 $$
$$ 2xc = 4a^2 + 4a \sqrt{(x-c)^2+y^2} - 2xc $$
$$ 2xc - 4a^2 + 2xc = 4a \sqrt{(x-c)^2+y^2} $$
$$ 4xc - 4a^2 = 4a \sqrt{(x-c)^2+y^2} $$
Divide both sides of the equation by 4:
$$ \frac{4xc - 4a^2}{4} = \frac{4a \sqrt{(x-c)^2+y^2}}{4} $$
$$ xc - a^2 = a \sqrt{(x-c)^2+y^2} $$
Square both sides of the equation to eliminate the square root:
$$ (xc - a^2)^2 = (a \sqrt{(x-c)^2+y^2})^2 $$
$$ x^2c^2 - 2xca^2 + a^4 = a^2 \cdot [(x-c)^2 + y^2] $$
$$ x^2c^2 - 2xca^2 + a^4 = a^2 \cdot (x^2 - 2xc + c^2 + y^2) $$
$$ x^2c^2 - 2xca^2 + a^4 = x^2a^2 - 2xca^2 + a^2c^2 + a^2y^2 $$
Then simplify:
$$ x^2c^2 + a^4 = x^2a^2 + a^2c^2 + a^2y^2 $$
Divide both sides of the equation by \(a^2\):
$$ \frac{x^2c^2 + a^4}{a^2} = \frac{x^2a^2 + a^2c^2 + a^2y^2}{a^2} $$
$$ \frac{x^2c^2}{a^2} + a^2 = x^2 + c^2 + y^2 $$
Move the known terms to the right side and the unknowns to the left:
$$ \frac{x^2c^2}{a^2} - x^2 - y^2 = c^2 - a^2 $$
Factor out \(x^2\):
$$ x^2 \cdot (\frac{c^2}{a^2} - 1) - y^2 = c^2 - a^2 $$
$$ x^2 \cdot (\frac{c^2 - a^2}{a^2}) - y^2 = c^2 - a^2 $$
At this point, knowing that \(c > a\), we set c^2 - a^2 = b^2
$$ x^2 \cdot (\frac{b^2}{a^2}) - y^2 = b^2 $$
$$ \frac{x^2b^2}{a^2} - y^2 = b^2 $$
Explanation: Construct a rectangle with sides 2a and 2b centered at the hyperbola's center, then draw a diagonal to form a right triangle with "c" as the hypotenuse and "a" and "b" as the legs. By the Pythagorean theorem, \(c^2 = a^2 + b^2\). Therefore, \(c^2 - a^2 = b^2\).
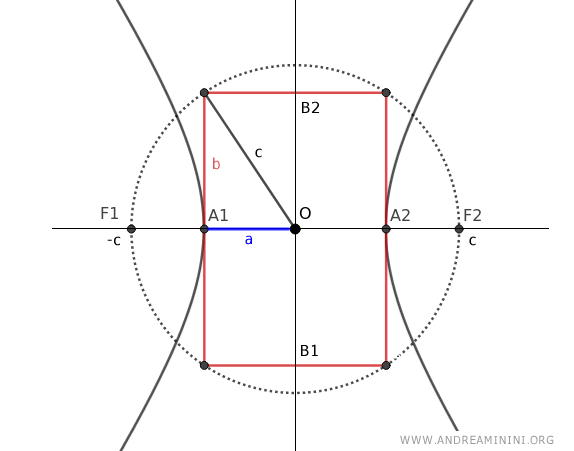
Then divide both sides of the equation by \(b^2\):
$$ \frac{1}{b^2} \cdot [\frac{x^2b^2}{a^2} - y^2] = \frac{1}{b^2} \cdot b^2 $$
$$ \frac{x^2b^2}{a^2b^2} - \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
The final result is the standard equation of the hyperbola when the foci are on the x-axis and the center of the hyperbola coincides with the origin \(O(0;0)\) of the Cartesian axes.
And so on.
