Distance Between Two Points
The distance is the shortest route from one point to another. To measure the Euclidean distance between two points in a plane, we use the Pythagorean theorem: $$ \overline{AB} = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} $$
Here, (x1, y1) and (x2, y2) are the Cartesian coordinates of points A and B in the plane.
A Practical Example
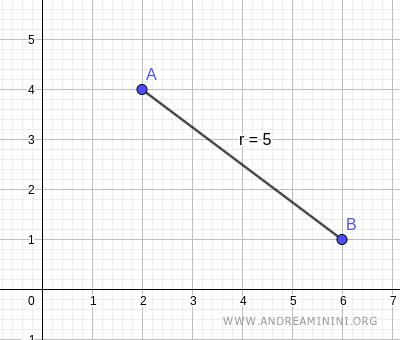
Consider the Cartesian coordinates of two points in space:
$$ A = \begin{pmatrix} 2 \\ 4 \end{pmatrix} = (2, 4) $$
$$ B = \begin{pmatrix} 6 \\ 1 \end{pmatrix} = (6, 1) $$
The distance between these two points is calculated as:
$$ \overline{AB} = \sqrt{(6-2)^2+(1-4)^2} $$
$$ \overline{AB} = \sqrt{4^2+(-3)^2} = \sqrt{16+9} = \sqrt{25} = 5 $$
Verify with Geogebra. The calculated distance is also confirmed by Geogebra.
The Proof
Let's consider two points in the plane:
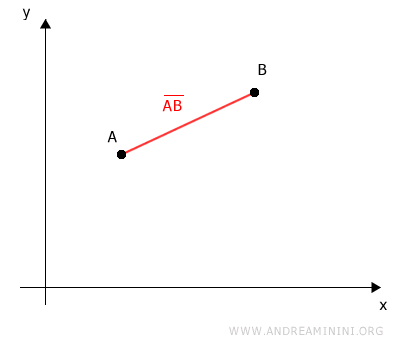
The segment AB represents the distance between points A and B.
We project the two points onto the Cartesian axes.
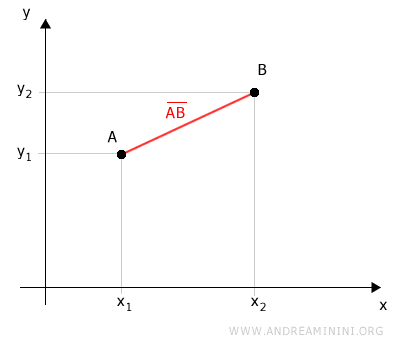
The projections form a right triangle ABC on the plane.
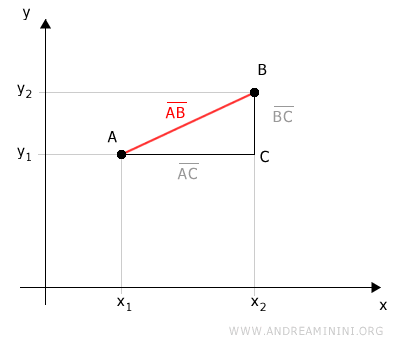
The segment AB is the hypotenuse of the right triangle ABC.
Therefore, to measure segment AB, we can use the Pythagorean theorem.
$$ \overline{AB} = \sqrt{\overline{AC}^2 + \overline{BC}^2} $$
Segment AC is the projection of segment AB onto the x-axis.
$$ \overline{AB} = \sqrt{(x_2-x_1)^2 + \overline{BC}^2} $$
Segment BC is the projection of segment AB onto the y-axis.
$$ \overline{AB} = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} $$
This is the formula we aimed to demonstrate.
Distance Between Two Points in Space
Given two points A $(x_A,\,y_A,\,z_A)$ and B $(x_B,\,y_B,\,z_B)$ in Cartesian space, the distance $AB$ is calculated as: $$ AB=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2+(z_A-z_B)^2}$$
The distance between two points in space corresponds to the length of the diagonal of a rectangular box whose edge lengths are the absolute differences along each coordinate axis: $|x_A-x_B|$, $|y_A-y_B|$, and $|z_A-z_B|$.

In other words, to find the distance between points $ A $ and $ B $, we apply the same formula used to compute the length of the diagonal $ AB $ of the box.
Note. If one of the points is the origin $O(0,0,0)$, the formula simplifies to the magnitude of the position vector of the other point. For example, to calculate the distance from point $ A $ to the origin $ O $, the formula becomes: $$ AO=\sqrt{x_A^2+y_A^2+z_A^2} $$
Example
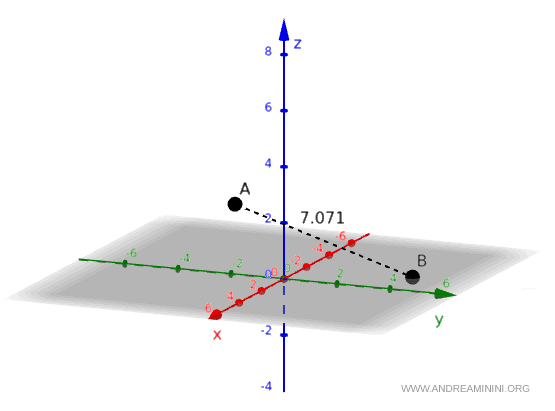
Consider the following two points in space:
$$ A(2,\,-1,\,3)$$
$$ B(-2,\,4,\,0) $$
The distance between them is:
$$ AB=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2+(z_A-z_B)^2} $$
$$ AB=\sqrt{(2-(-2))^2+((-1)-4)^2+(3-0)^2} $$
$$ AB=\sqrt{4^2+(-5)^2+3^2} $$
$$ AB=\sqrt{16+25+9} $$
$$ AB=\sqrt{50} \approx 7.071 $$
Thus, the distance between the two points is $ \sqrt{50} $.
Distance Measured with Polar Coordinates
The distance between two points in the plane can also be measured using the polar coordinates of the points: $$ \overline{AB} = \sqrt{r_1^2 + r_2^2 - 2r_1r_2 \cos (\alpha_2 - \alpha_1)} $$
Here, (r1, α1) and (r2, α2) are the polar coordinates of the points.
Example
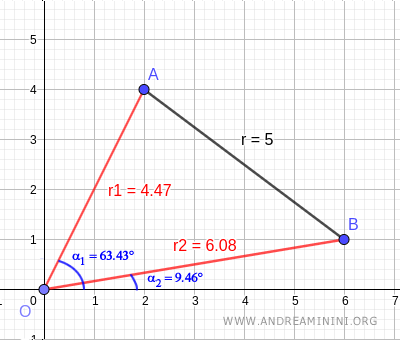
Two points in the plane have the following polar coordinates:
$$ A [ \ 4.47 \ , \ 63.43° \ ] $$
$$ B [ \ 6.08 \ , \ 9.46° \ ] $$
Graphically, this looks like:
The distance between points A and B is:
$$ \overline{AB} = \sqrt{r_1^2 + r_2^2 - 2r_1r_2 \cos (\alpha_2 - \alpha_1)} $$
$$ \overline{AB} = \sqrt{(4.47)^2 + (6.08)^2 - 2 \cdot (4.47) \cdot (6.08) \cos (9.46° - 63.43°)} $$
$$ \overline{AB} = \sqrt{19.98 + 36.97 - 54.36 \cdot \cos (-53.97°)} $$
$$ \overline{AB} = \sqrt{25} = 5 $$
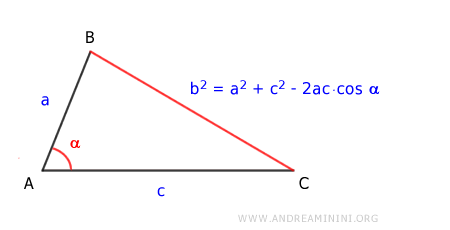
Proof. The distance formula using polar coordinates is derived from the cosine rule in a triangle.
And so on.
