Lines

What is a line?

A line is a straight path of points that extends infinitely in both directions without ever curving.

The line is a fundamental geometric object in Euclidean geometry.

According to the first postulate of Euclid, a unique line can be drawn through any two distinct points in space.

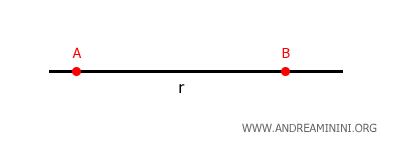
Lines are typically represented by lowercase letters, while points are denoted by uppercase letters.

Note. From this, we can infer that a line can never curve, because given two pairs of distinct points on the plane (A, B) and (B, C), they belong to a single line only if they are all aligned.

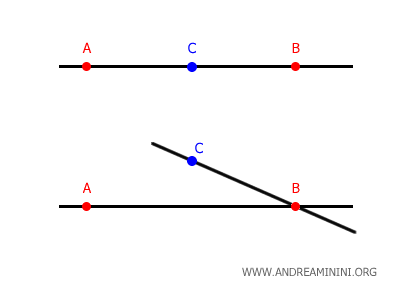
According to the second postulate of Euclid, a line is a segment that can be extended infinitely in both directions.

Thus, a line has neither a starting point nor an ending point.

Note. This distinguishes a line from a segment, which has two endpoints: a beginning and an end.

Given any two points on a line, there is always at least one other point between them.

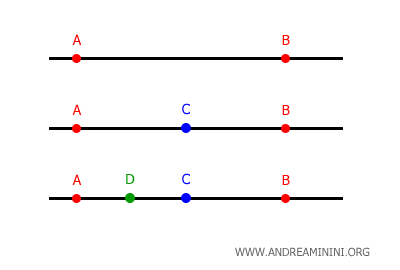
For this reason, a line is considered a dense set.

Note. There is a one-to-one correspondence between the points on a line and the set of real numbers. Both are sets with an infinite number of elements of the same density.

Several properties of lines are derived from Euclid's first two postulates.

When two or more lines pass through the same point, they are called intersecting lines or concurrent lines.

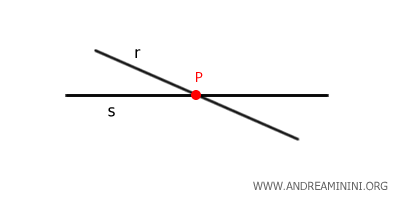
Infinite lines can pass through a single point.

The set of lines passing through a point is called a pencil of lines.

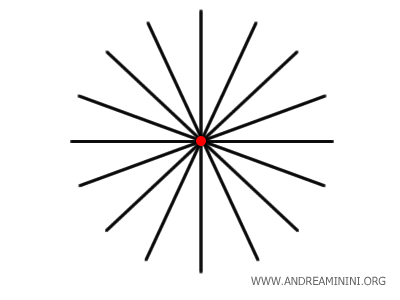
Note. Knowing that a line is a set of points, we deduce that a line contains at least one point. To define a line, at least two points are needed, so we deduce that infinite lines pass through any given point.

Each plane contains infinitely many points, so it also contains infinitely many lines.

To define a plane, at least three non-collinear points are required.

In three-dimensional space, a line can be defined as the intersection of two planes.

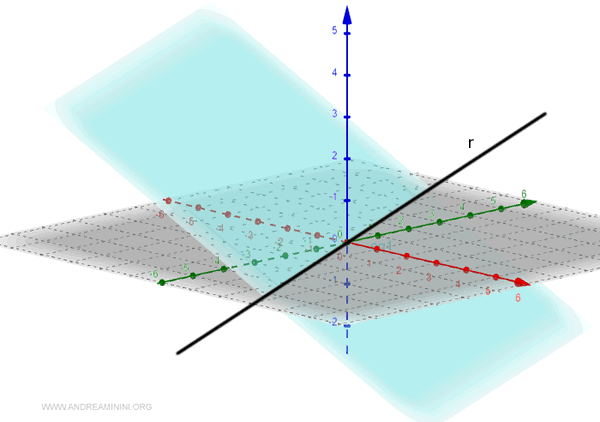
Note. This concept is a simplification of a much more general idea that can be extended to many more dimensions in advanced mathematics.

On a line, it is always possible to define a direction.

A line with a defined direction is called a directed line.

In the Cartesian plane, a line can be defined by a linear equation

$$ y = mx + b $$

Where

• "y" is the value of the vertical coordinate of any point on the line
• "x" is the value of the horizontal coordinate of any point on the line
• "m" is the slope of the line, representing the line's steepness, i.e., m = y/x
• "b" is the y-intercept, the point where the line intersects the y-axis (when x = 0).

Graphically, the line's equation on the Cartesian plane is represented as follows:

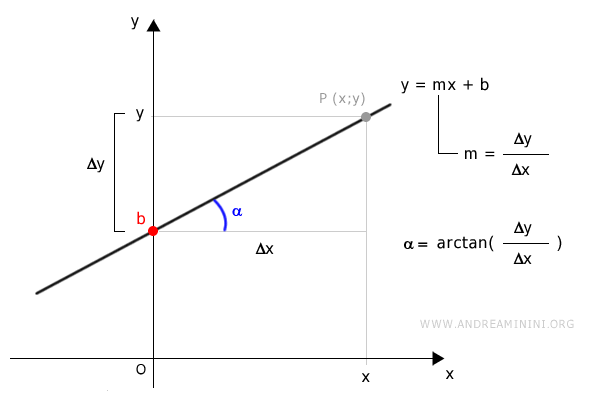
Given any two points on the line, it is always possible to find the line's equation using the formula for the slope and the line equation itself.

And so on.