Lines Intersected by a Transversal
When two distinct lines r and s are intersected by a transversal line t at two points, they create eight angles on the plane.
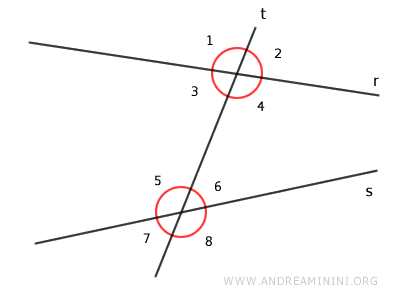
The names of these angles vary based on their positions relative to the lines.
Firstly, the angles are categorized into two types: interior and exterior angles.
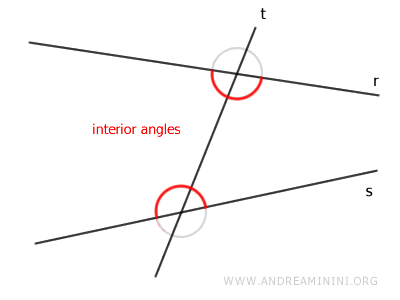
- Interior Angles
These are the angles located between the two lines r and s.
- Exterior Angles
These are the angles that lie outside the two lines.
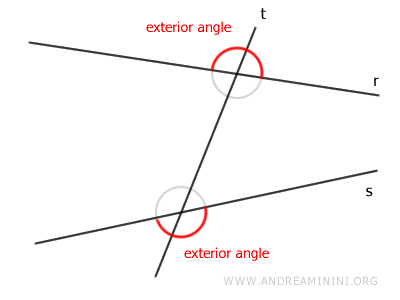
Thus, there are four interior angles and four exterior angles.
Depending on their relative positions to the transversal, the angles are classified as alternate, consecutive, or corresponding angles.
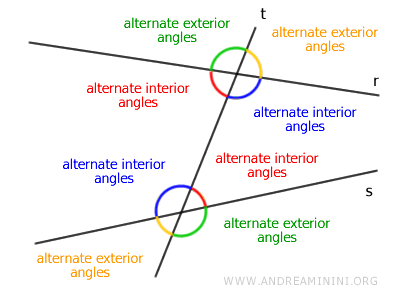
- Alternate Angles
Alternate angles are non-adjacent and located on opposite sides of the transversal. Both angles must be either interior or exterior. If one is interior, the other must also be interior.
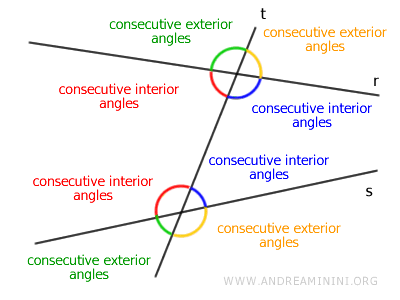
- Same-Side Angles
Same-Side angles (or consecutive angles) are non-adjacent and located on the same side of the transversal. Both must be either interior or exterior.
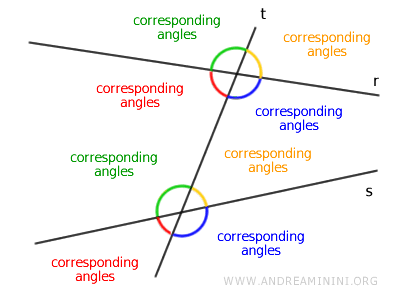
- Corresponding Angles
Corresponding angles are non-adjacent and located on the same side of the transversal. One must be interior and the other exterior.
And so forth.
