Parallel Postulate

The parallel postulate, also known as Euclid's fifth postulate, states:

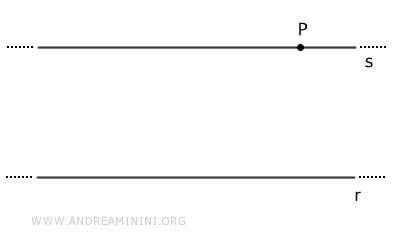
Given a line r and a point P not on the line, there exists exactly one line parallel to r that passes through point P.

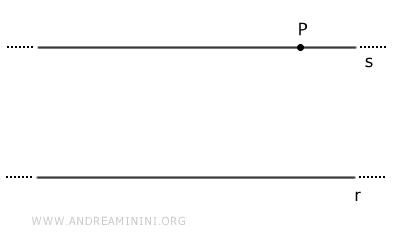
This is considered a postulate because the uniqueness of the parallel line is not derived from other theorems or properties of the line. It is accepted as a fundamental truth.

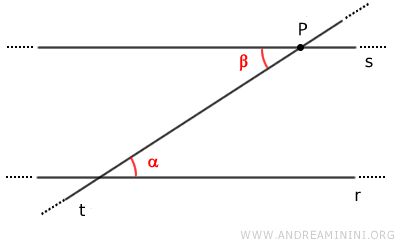
However, the existence of a line parallel to r passing through point P can be demonstrated using the parallel lines theorem by finding a pair of congruent alternate interior angles α≅β.

Note: This postulate is known as Euclid's fifth postulate. However, its formulation is attributed to Proclus, a Byzantine mathematician and philosopher who lived in the 5th century AD.

The Proof

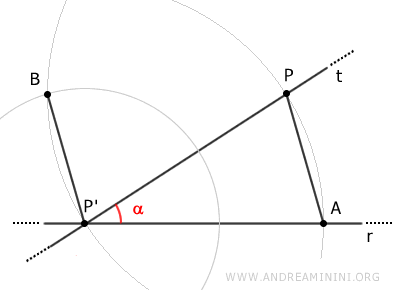
Consider a line r and a point P in the plane that does not lie on the line.

Choose a point P' on the line.

Then draw a line t passing through points P' and P.

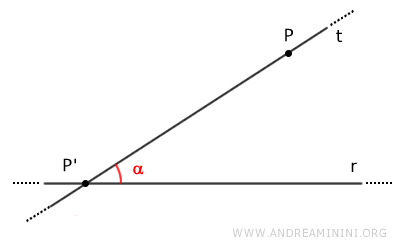
Line t forms an interior angle alpha (α) with line r.

Draw an arc centered at P' with radius PP' that intersects line r at point A.

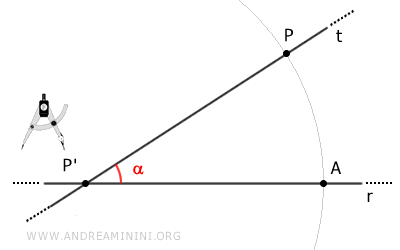
Center the compass on point P and with the same radius (PP'), draw a second arc that passes through point P'.

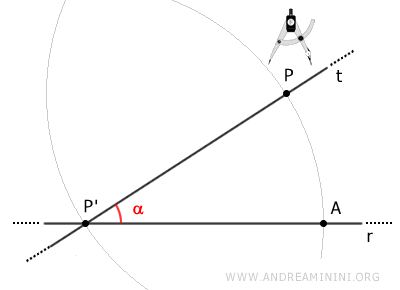
Connect points A and P with a segment AP.

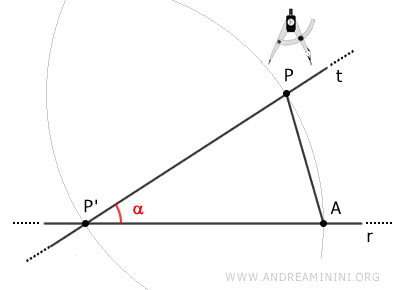
Draw a third arc centered at P' with radius AP that intersects the second arc at point B.

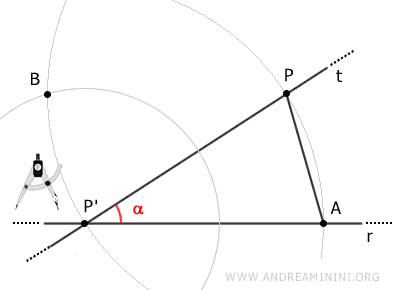
Then connect points P' and B with segment BP'.

Finally, draw a line s passing through points B and P.

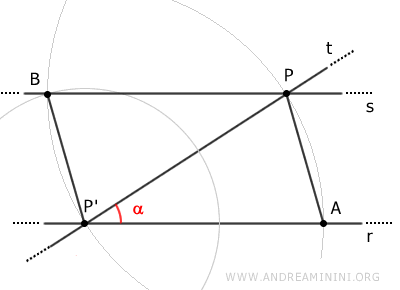
Two triangles, APP' and BPP', are formed between lines r and s.

According to the third criterion for triangle congruence, the triangles APP' and BPP' are congruent because they have sides of equal length.

$$ APP' \cong BPP' $$

Since they are congruent, triangles APP' and BPP' have congruent angles in corresponding positions.

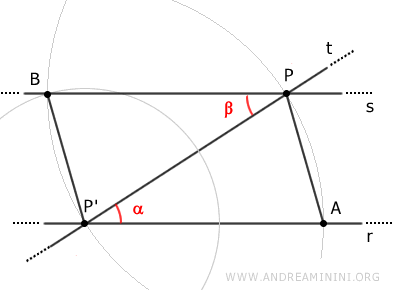
Therefore, angle alpha is congruent to angle beta.

$$ \alpha \cong \beta $$

Angles alpha and beta are congruent alternate interior angles (α≅β).

Thus, by the parallel lines theorem, lines r and s are parallel.

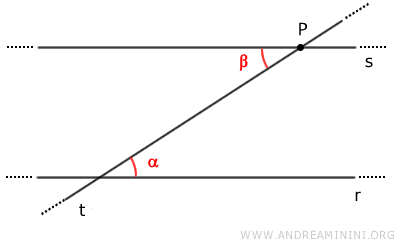
This demonstrates the existence of line s parallel to line r passing through point P

Note: As mentioned earlier, the uniqueness of the parallel line s cannot be proven through other properties. Therefore, it is accepted as a postulate.

Why can't the uniqueness be proven?

Even Euclid himself recognized that the so-called fifth postulate seemed less self-evident and less “obvious” than his other axioms. For this reason, he sought to invoke it as little as possible, and only when absolutely necessary.

For centuries, mathematicians attempted to prove the fifth postulate from the first four, but in vain. It is independent. Every purported proof inevitably relied - often unwittingly - on assumptions that were logically equivalent to the postulate itself.

In trying to prove that exactly one parallel passes through a point external to a given line (uniqueness), as Euclid claimed and as intuition suggested, mathematicians even experimented with altering the postulate itself.

But instead of encountering inconsistency or contradiction, they uncovered an entire alternative geometric framework that was internally coherent.

Note. Girolamo Saccheri attempted a proof by contradiction: he constructed a hypothetical geometry omitting the fifth postulate, hoping to derive an inconsistency. Yet no contradiction emerged.

These efforts eventually gave rise, in the 19th century, to the development of non-Euclidean geometries, where the fifth postulate is replaced with a different assumption:

• Hyperbolic geometry (Lobachevsky, Bolyai): In this geometry, through a point external to a given line, infinitely many parallel lines can be drawn, and the sum of the internal angles of any triangle is less than 180°.
  

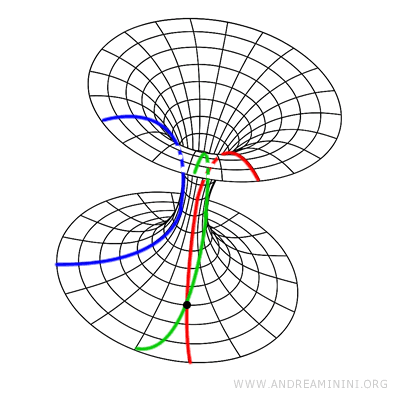
  Note. The pioneering work of Saccheri, Lobachevsky, and Bolyai was not, in itself, sufficient to establish the logical consistency of hyperbolic geometry. This was later accomplished by Felix Klein and Henri Poincaré, who constructed models of hyperbolic geometry within Euclidean geometry - thereby demonstrating that if Euclidean geometry is consistent, so too is hyperbolic geometry. In Klein’s model, for example, the "plane" is represented by the interior of a circle, while "lines" are represented by chords of that circle.

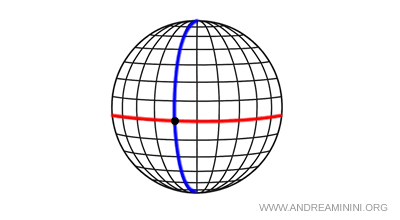
• Elliptic geometry (Riemann): In this geometry, no parallel line can pass through a point external to a given line. Moreover, the sum of a triangle’s internal angles exceeds 180°. On a sphere, for example, no parallel lines exist because all "lines" are great circles, which necessarily intersect.
  

The discovery of non-Euclidean geometries stands as one of the great mathematical achievements of the 19th century.

It revealed that many properties we had once thought "universal" in fact depend on the fifth postulate, and that Euclid’s axioms are not the only foundation upon which a consistent geometry can be constructed.

It also helped usher in the modern understanding of an axiom - not as an absolute truth, but as an assumption that defines a given mathematical framework.

More broadly, the emergence of non-Euclidean geometries demonstrated that the very concept of space is not absolute, and that space itself can be conceptualized in multiple, equally valid ways - an insight with far-reaching consequences for both mathematics and physics.

Simply put, the fifth postulate helps us understand that there is no single “true” geometry; rather, there are many possible geometries, of which Euclidean geometry is just one special case. It remains an open question, however, which geometry best reflects physical reality. According to Einstein’s theory of relativity, gravity warps space. Near black holes, for example, this curvature becomes extreme. Thus, to understand the overall geometry of the universe, we must determine whether it is flat (Euclidean) or curved (non-Euclidean). Current evidence suggests that, if any curvature exists, it is extremely slight - meaning the universe appears nearly flat.

And so the story continues.