Theorem of Parallel Line Pencils

If a pencil of parallel lines is intersected by two transversal lines, congruent segments on one transversal correspond to congruent segments on the other transversal.

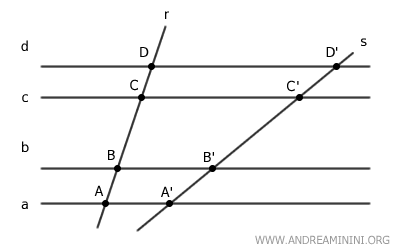
A Practical Example

For instance, consider a pencil of parallel lines (a, b, c, d) and two transversal lines r and s.

Note. A pencil of parallel lines refers to a set of lines that are parallel to each other. For example, the lines a, b, c, and d are all parallel to each other.

The parallel lines intersect the transversal r at points A, B, C, and D, and intersect the transversal s at points A', B', C', and D'.

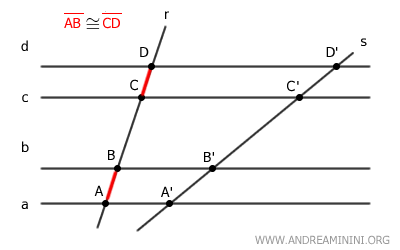
Assume the segments AB and CD on transversal r are congruent, meaning they have the same length AB≅CD.

$$\overline{AB} \cong \overline{CD}$$

According to the theorem of the parallel lines pencil, these congruent segments AB≅CD correspond to congruent segments A'B'≅C'D' on the other transversal s.

$$\overline{A'B'} \cong \overline{C'D'}$$

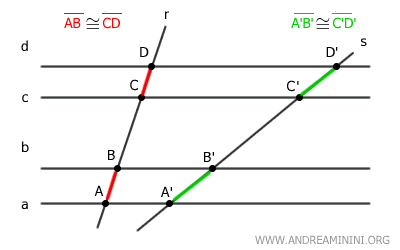
The endpoints of the corresponding segments on the other transversal A'B' and C'D' are determined by the parallel lines that intersect the same endpoints of segments AB and CD on the first transversal.

For example, line "a" passes through both point A and point A', which are the lower endpoints of segments AB and A'B'.

The Proof

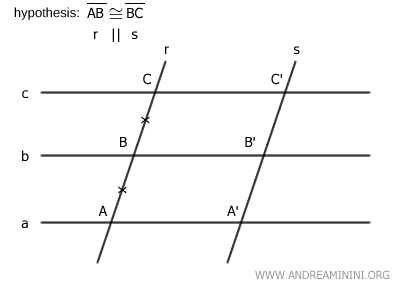
Initially, consider a pencil of parallel lines (a, b, c) and two transversal lines r and s with two corresponding congruent segments AB≅BC on transversal r.

$$\overline{AB} \cong \overline{AB}$$

I need to prove that there are two corresponding congruent segments A'B'≅B'C' on transversal s (thesis).

To prove the theorem, I consider two cases: the transversals are parallel or intersecting.

A] The Transversals are Parallel

In this case, by initial assumption, the lines r and s are parallel to each other, i.e., r||s.

Since the transversals are parallel, I deduce that the segments AA', BB', and CC' are congruent, i.e., AA'≅BB'≅CC'.

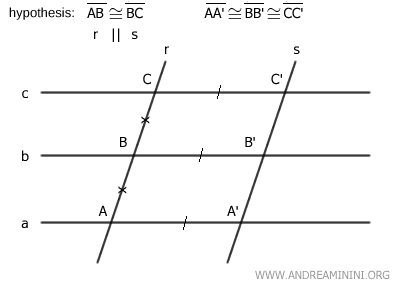
The figure AA'B'B is a parallelogram because both pairs of opposite sides are parallel by the definition of a pencil of parallel lines a||b||c and the initial assumption r||s.

Similarly, the figure BB'C'C is also a parallelogram for the same reasons.

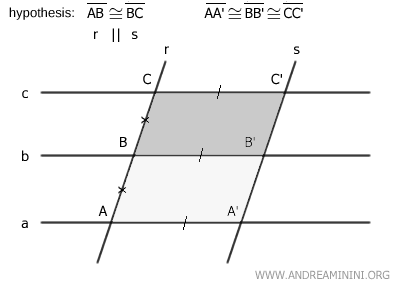
Knowing that the slanted sides of the two parallelograms AB≅BC are congruent by initial assumption and their bases are also congruent AA'≅BB', I deduce that the two parallelograms are congruent AA'B'B≅BB'C'C.

$$AA'B'B \cong BB'C'C$$

Therefore, the two parallelograms have congruent sides and angles in the same order.

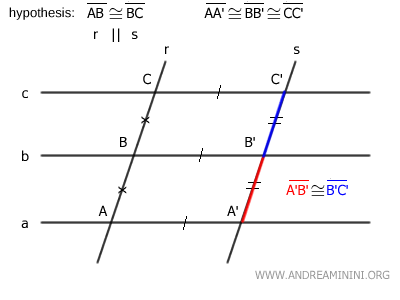
In particular, it is important to note that the slanted sides AB≅A'B' and BC≅B'C' are congruent.

$$\overline{AB} \cong \overline{A'B'}$$

$$\overline{BC} \cong \overline{B'C'}$$

Knowing from the initial assumption that AB≅BC, I deduce by the transitive property that the sides A'B'≅B'C' are also congruent.

$$\overline{A'B'} \cong \overline{B'C'}$$

In conclusion, I have shown that the corresponding segments A'B' and B'C' on transversal s are congruent if the two transversals are parallel.

B] The Transversals are Not Parallel

In this case, by initial assumption, the lines r and s are intersecting (not parallel).

I draw the line s' parallel to line s, making it intersect line r at point C.

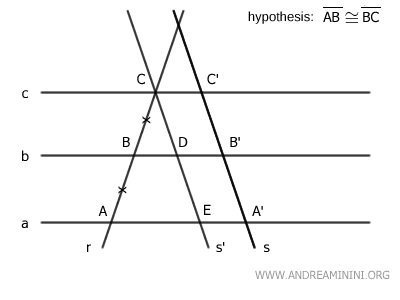
Then I draw a second line s'' parallel to s passing through point B.

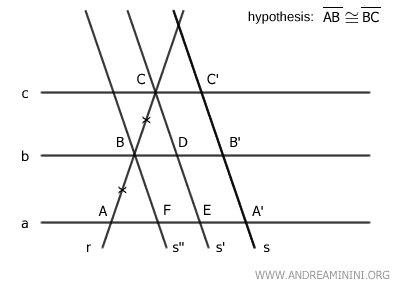
The figure CDB'C' is a parallelogram and, by definition, has congruent opposite sides.

Thus, I deduce that CD≅B'C'.

$$\overline{CD} \cong \overline{B'C'}$$

The figure BFA'B' is also a parallelogram and has congruent opposite sides.

Thus, I deduce that BF≅A'B'.

Now I analyze the two triangles ABF and BCD.

The two triangles have one congruent side AB≅BC by initial assumption.

Additionally, they have corresponding angles α≅α' congruent by the theorem of parallel lines, because the parallel lines "a" and "b" are cut by the transversal line s''.

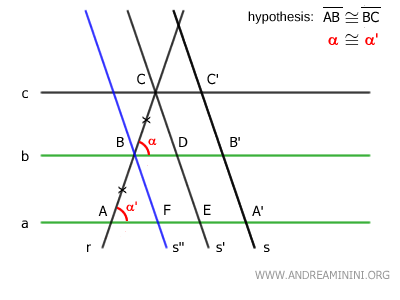
Similarly, the corresponding angles β≅β' are congruent by the theorem of parallel lines, because the parallel lines s' and s'' are cut by the transversal line r.

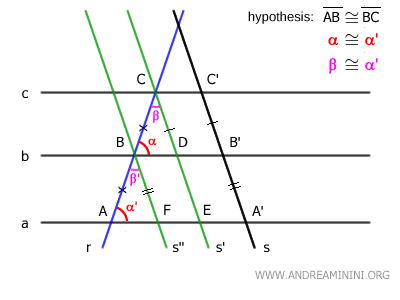
The triangles ABD≅BCD are congruent by the second congruence criterion (ASA) because they have one congruent side AB≅BC and two congruent angles α≅α' and β≅β'.

Therefore, the two triangles have all sides and angles congruent.

In particular, it is useful to know that the sides BF≅CD are congruent.

$$\overline{BF} \cong \overline{CD}$$

Knowing that CD≅B'C' and BF≅A'B' by the transitive property, I deduce that A'B'≅B'C'.

$$\overline{A'B'} \cong \overline{B'C'}$$

In conclusion, I have shown that the corresponding segments A'B' and B'C' on transversal s are congruent if the two transversals are intersecting.

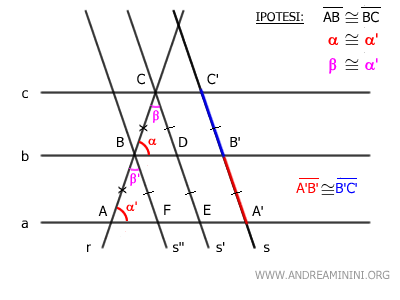
And so on.