Pencil of Lines

What is a Line Pencil?

A line pencil is a collection of lines in a plane defined by a specific selection criterion.

There are two types of line pencils: proper line pencil and pencil of parallel lines.

Pencil of Parallel Lines

A pencil of parallel lines consists of all lines parallel to a given line r in the plane.

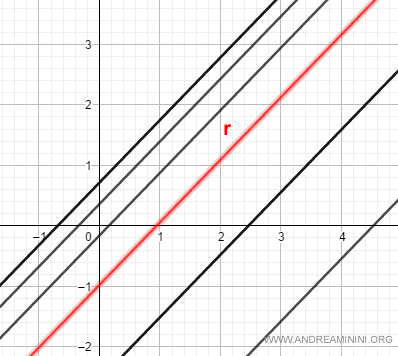
The Cartesian equation of an improper line pencil is:

$$ ax + by + c = 0 $$

where the coefficients a and b are non-zero.

Each line is identified by a specific value of c.

Note: The line r, which all other lines are parallel to, is also characterized by a specific value of c.

Alternatively, the equation of a parallel lines pencil can be written in explicit form as:

$$ y = mx + q $$

In this form, each line is characterized by a different value of the term q.

For q=0, the line passes through the origin.

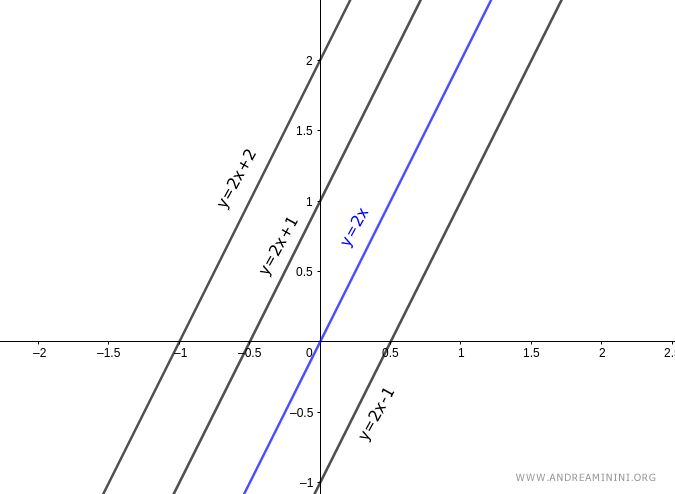
Note: The term q represents the y-intercept, which is the point where the line crosses the y-axis when x=0.

The parametric equation of the line pencil is:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$

In this case, each line of the parallel lines pencil is defined by varying the combination (x₀, y₀).

The direction vector (l, m) remains the same for all parallel lines.

Example

The Cartesian equation of a line is:

$$ 2x + 3y - 12 = 0 $$

By changing the parameter c=12 to other values, we get an infinite number of parallel lines in the pencil.

 

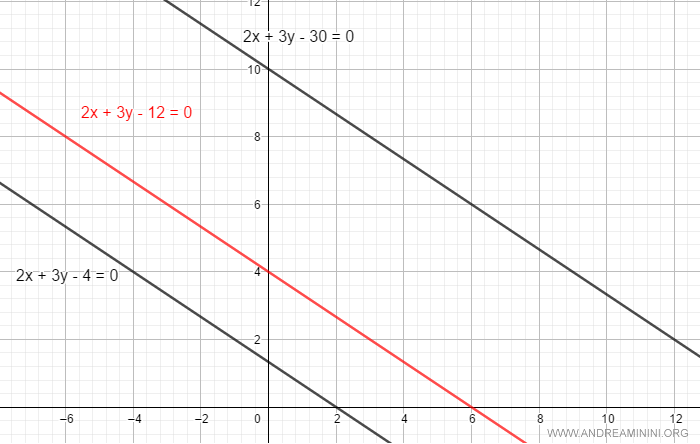
We can also write the line pencil as a parametric equation:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ -\frac{2}{3} \end{pmatrix} $$

By changing the parameter (0,4) of the intercept, we obtain all the other lines, keeping the direction vector unchanged.

The result remains consistent.

Line Pencil

A proper line pencil consists of all lines passing through a specific point (A) in the plane, known as the pencil center.

The equation of a proper line pencil centered at a point with coordinates (x₀, y₀) is:

$$ y - y_0 = m \cdot (x - x_0) $$

By varying the slope m ∈ R, we get all the lines in the proper pencil passing through point A, except for the line parallel to the y-axis.

Note: The line parallel to the y-axis cannot be expressed with the explicit equation y = mx because no value of m can provide this equation. For lines parallel to the y-axis, we use the equation x = x₀. $$ x = x_0 $$

Therefore, the complete pencil of lines is described by the equations:

$$ \begin{cases} y - y_0 = m \cdot (x - x_0) \\ \\ x = x_0 \ \ \ \text{if the line is parallel to the y-axis} \end{cases} $$

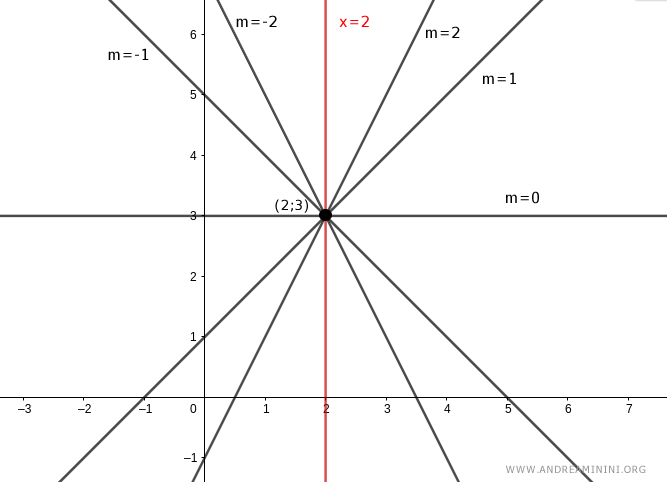
< Example

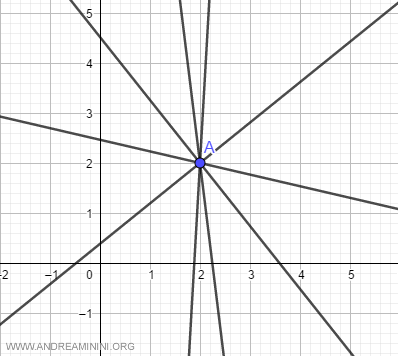
Let's consider a pencil center C:

$$ C = \begin{pmatrix} x_0 = 2 \\ y_0 = 3 \end{pmatrix} $$

The equations for the pencil centered at C are:

$$ y - y_0 = m \cdot (x - x_0) $$

$$ x = x_0 $$

Given x₀ = 2 and y₀ = 3, the equations for the pencil become:

$$ y - 3 = m \cdot (x - 2) $$

$$ x = 2 $$

The first equation, y - 3 = m(x - 2), represents all lines with varying slopes m, except for the line parallel to the y-axis.

The second equation, x = 2, represents the line parallel to the y-axis (shown in red).

Line Pencil as a Linear Combination of Two Lines

A proper or improper line pencil can also be generated using a linear combination of two lines:

$$ r: ax + by + c = 0 $$

$$ s: a'x + b'y + c' = 0 $$

The linear combination of the two lines is:

$$ p \cdot (ax + by + c) + q \cdot (a'x + b'y + c') = 0 $$

Dividing both sides by p, we get:

$$ ax + by + c + \frac{q}{p} \cdot (a'x + b'y + c') = 0 $$

Letting $ k = \frac{q}{p} $, we have:

$$ ax + by + c + k \cdot (a'x + b'y + c') = 0 $$

$$ ax + by + c + a'xk + b'yk + c'k = 0 $$

Each value of $ k $ corresponds to a unique line in the pencil.

Note: This linear combination represents all lines in the pencil except for the line $ s: a'x + b'y + c' = 0 $, as no value of $ k $ corresponds to line $ s $. $$ ax + by + c + k \cdot (a'x + b'y + c') = 0 $$

Highlighting the common factors x and y:

$$ (ax + a'xk) + (by + b'yk) + c + c'k = 0 $$

$$ (a + a'k) \cdot x + (b + b'k) \cdot y + c + c'k = 0 $$

This is the general equation of the line pencil.

A line pencil can be either proper or improper:

• Proper Line Pencil
  This occurs if the ratio of the coefficients a and b in the equations is different $$ \frac{a}{b} \ne \frac{ a'}{b'} $$
• Improper Line Pencil
  This occurs if the ratio of the coefficients a and b in the equations is the same, as the two lines are either parallel or coincident. $$ \frac{a}{b} = \frac{a'}{b'} $$

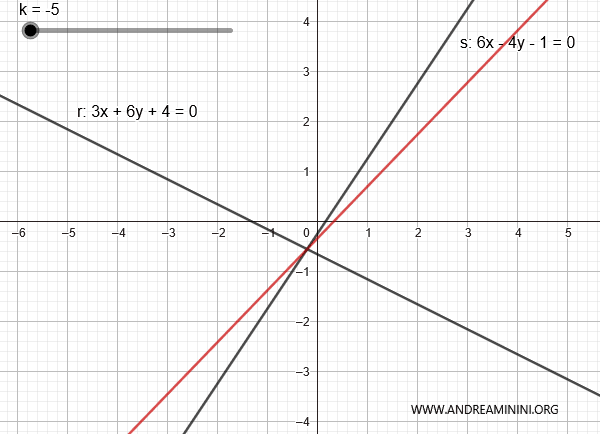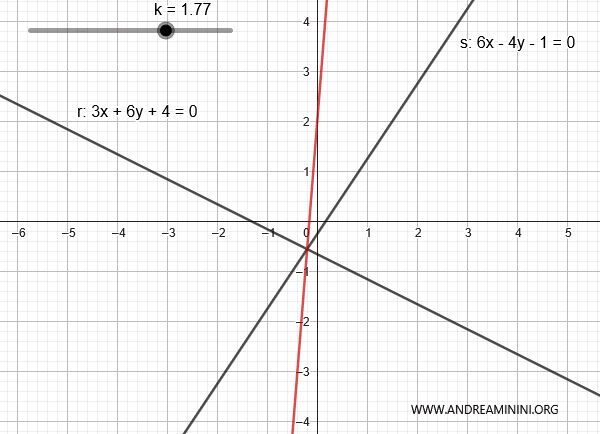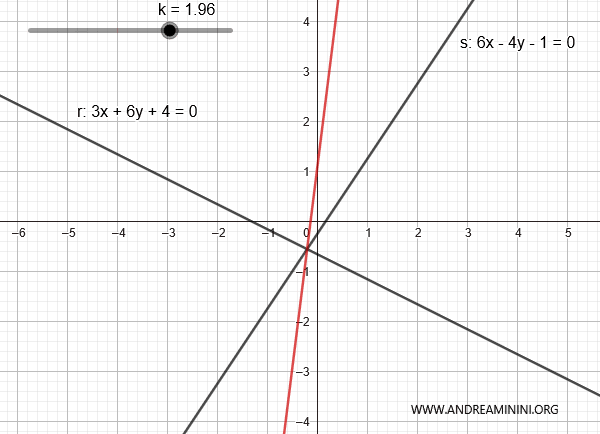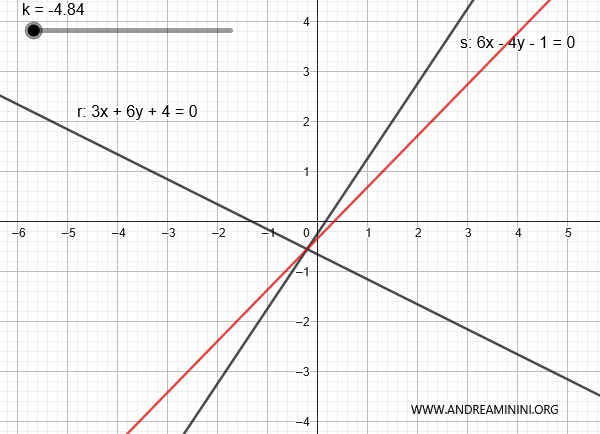
Example

Consider the lines:

$$ r: 3x + 6y + 4 = 0 $$

$$ s: 6x - 4y - 1 = 0 $$

Here is the representation of the two lines in the plane:

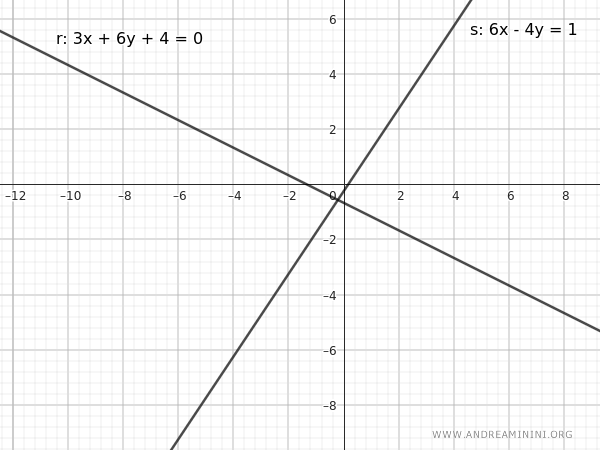
In this case, they intersect because the ratio of the coefficients is different:

$$ \frac{a}{b} \ne \frac{a'}{b'} $$

$$ \frac{3}{6} \ne \frac{6}{4} $$

Therefore, this is a proper line pencil.

The combination of the two lines is:

$$ 3x + 6y + 4 + k \cdot (6x - 4y - 1) = 0 $$

$$ 3x + 6y + 4 + 6xk - 4yk - k = 0 $$

$$ (3x + 6xk) + (6y - 4yk) + 4 - k = 0 $$

$$ (3 + 6k) \cdot x + (6 - 4k) \cdot y + 4 - k = 0 $$

By varying k, we can generate the other lines in the pencil, except for line s.