Pencil of Parallel Lines

A pencil of parallel lines is the set of all lines in the plane that are parallel to a given line r.

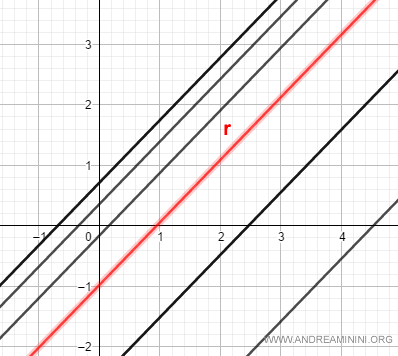
A pencil of parallel lines consists of an infinite number of parallel lines.

Typically, it is graphically represented by showing just one line as an example, $y = mx+q$, known as the base line of the bundle.

By varying the constant term $q$, which is the y-intercept, all the other lines parallel to the base line can be obtained.

$$y = mx+q$$

Alternatively, the pencil of parallel lines can also be represented by the implicit equation of the base line

$$ax+by+k = 0$$

In this case, by varying k, all the lines parallel to the base line are obtained.

Example. The equation $y = 2x+q$ is the base line of a bundle that includes all lines parallel with a slope of m=2. When q=0, the line passes through the origin of the Cartesian plane $y=2x$. To get all the other parallel lines, you simply assign different values to the constant term q. For example, if q=5, you get the equation of the line $y=2x+5$, if q=-5, you get $y=2x-5$, if q=10, you get $y=2x+10$, and so on.

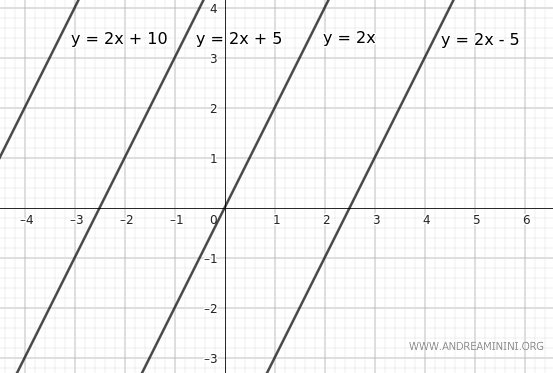
The Implicit (Cartesian) Equation of the Pencil of Parallel Lines

The Cartesian equation (implicit or general) of the pencil of parallel lines is as follows:

$$ax + by + c = 0$$

Where a and b are the coefficients of the line, they are constant non-zero values that determine the slope of the lines in the bundle.

The constant term c, on the other hand, is a variable parameter that allows for the different lines within the same bundle to be obtained. 

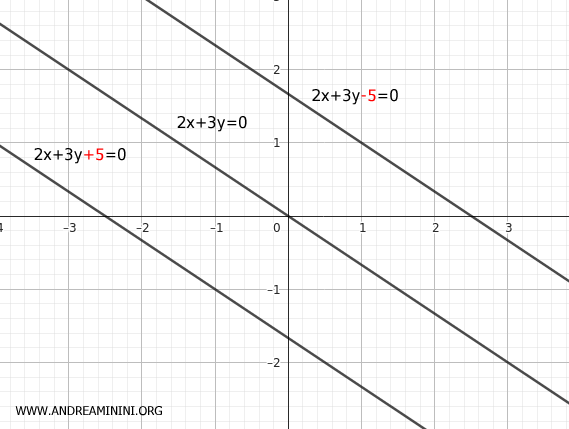
In other words, each line in the pencil of parallel lines is characterized by a specific value of the constant term $c$ which determines the position and distance of the line relative to the other parallel lines.

In the particular case where the constant term is zero (c=0), the line passes through the origin of the Cartesian plane at the point (x;y)=(0;0).

Note. The main line r, the "base" line to which all other lines are parallel, also has a specific and unique value of the constant term c. For example, if we consider the base line of the bundle as the equation $2x+3y-5=0$, the constant term is $c=-5$.

There are two special cases worth mentioning:

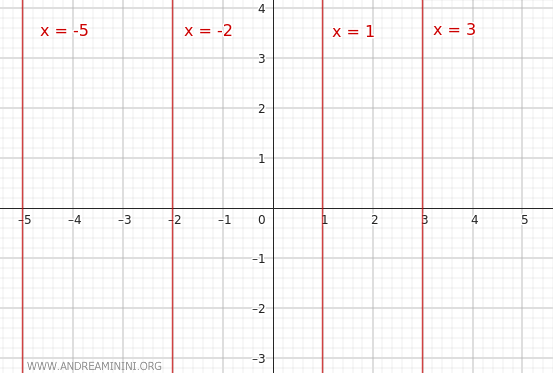
• $x=k$
  This is the equation of a pencil of parallel lines parallel to the y-axis. In this configuration, each line in the bundle has a different x-intercept determined by the value of k, but no slope relative to the y-axis, resulting in vertical lines. In the particular case where x=0, the line coincides with the y-axis. Examples include x=-5, x=-2, x=1, x=3, etc.
  
• $y=k$
  This equation represents a pencil of parallel lines parallel to the x-axis. Each line has a different y-intercept, depending on the value of k, and are horizontal lines with no slope relative to the x-axis. In the particular case where y=0, the line coincides with the x-axis. Other examples include y=3, y=1, y=-1, y=-2, etc.
  

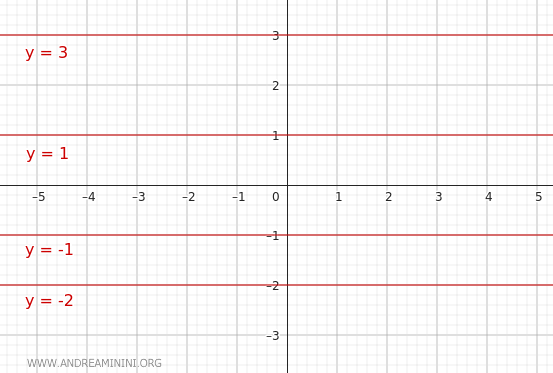
These two special cases are useful for describing sets of lines that maintain a fixed direction while shifting parallel along the other axis.

The Equation of the Bundle of Lines in Explicit Form

Alternatively, the equation of the pencil of parallel lines can also be expressed in explicit form as:

$$y = mx + q$$

In this case, each line in the bundle has a unique value of q.

If q=0, the line intersects the origin.

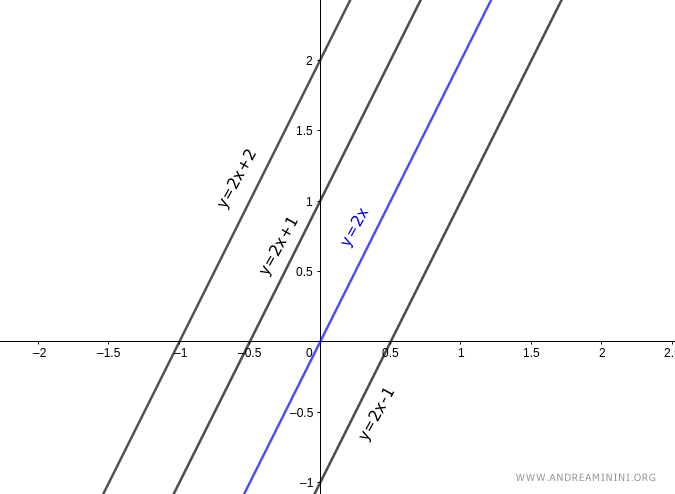
Note. The term q is the constant term of the equation and represents the y-intercept at x=0.

The Parametric Equation

Another representation is given by the parametric equation

$$\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \end{pmatrix}$$

Where the combination (x₀,y₀) varies for each line in the bundle, while the direction vector (l,m) remains constant.

Example

Given the line:

$$2x +3y - 12 = 0$$

By varying c, parallel lines in the pencil of parallel lines are generated.

 

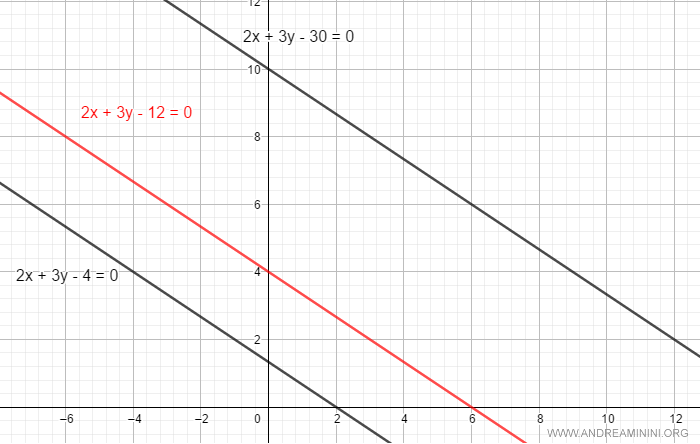
In parametric form, the same line is represented as:

$$\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \end{pmatrix}$$

$$\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ -\frac{2}{3} \end{pmatrix}$$

By modifying the intercept (0,4) and keeping the direction vector constant, all the lines in the bundle are generated.

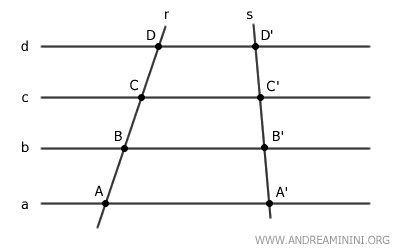
The Transversal of the Pencil of Parallel Lines

The transversal of the bundle of lines is a line that intersects all the parallel lines in the pencil of parallel lines.

For example, line r is a transversal of the bundle of lines.

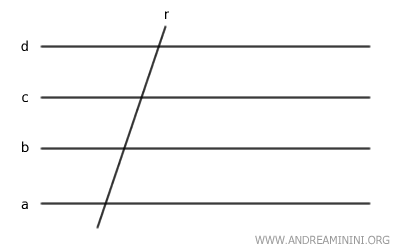
When two distinct transversals intersect a pencil of parallel lines, the intersection points of the transversals with the parallel lines are called corresponding points.

For example, points A and A' are two corresponding points.

Segments that have corresponding points as endpoints on the same transversal are called corresponding segments.

For example, segments AB and BC are two corresponding segments.

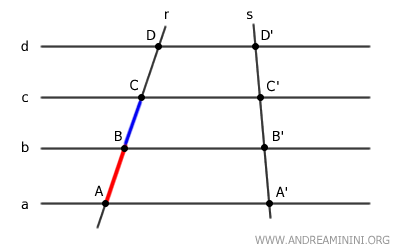
Similarly, segments A'B' and B'C' on the second transversal are also corresponding segments.

According to the Thales' Theorem, when a bundle of parallel lines intersects two transversal lines, there is a direct proportionality between the corresponding segments of one transversal and those of the other.

For example, segment AB is to segment CD as segment A'B' is to segment C'D'

$$AB:CD = A'B':C'D'$$

This direct proportionality is called Thales' correspondence.

And so on.