Equation of a Line Through the Origin

The equation of a line that passes through the origin O(0,0) in the Cartesian plane is: $$ y = mx $$ 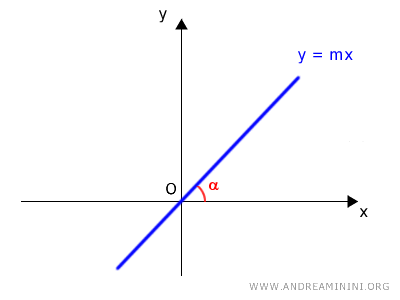an example of a line passing through the origin of the plane

This simple equation is derived from the slope-intercept form of a line.

$$ y = mx + c $$

Here, the y-intercept is zero, so $ c = 0 $.

$$ y = mx $$

Therefore, the y component depends directly on the slope (m) and the value assigned to the x component.

$$ m = \frac{y}{x} $$

The slope $ m $ represents the steepness of the line and indicates its angle relative to the x-axis.

Note: The equation y=mx is likely the most straightforward and intuitive for lines passing through the origin, as it reflects the direct linear relationship between y and x without any vertical offset. The variables $ x $ and $ y $ are directly proportional because their ratio remains constant, $ m = \frac{y}{x} $.

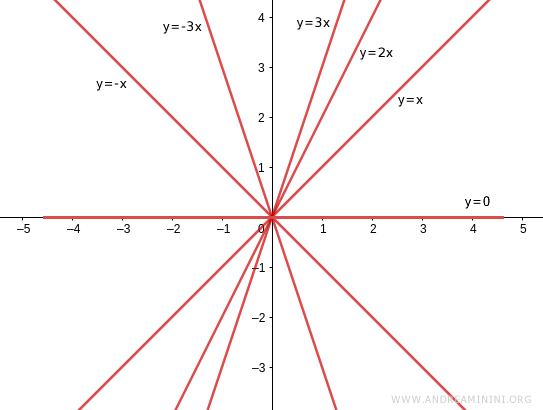
The slope m can take any real value.

If m>0 is positive, the line slopes upward from left to right. Here, the angle between the line and the x-axis is acute.
If m<0 is negative, the line slopes downward. In this case, the angle between the line and the x-axis is obtuse.
If m=0 is zero, the line is horizontal and coincides with the x-axis. The equation of the line is $ y = 0 $ and the angle between the line and the x-axis is zero.

the family of lines passing through the origin

Additionally, if the value of m is undefined, the line becomes vertical and coincides with the y-axis.

To represent this specific case, we use the equation $ x = 0 $.

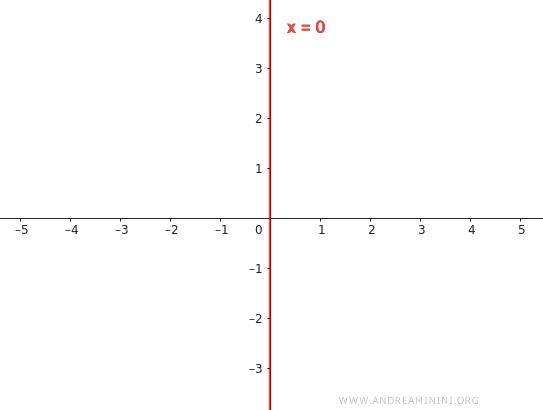
the equation of the line passing through the origin

Explanation: When the slope m is undefined or infinite, the line can no longer be described by the explicit form y=mx. To represent a line parallel to the y-axis, we use the equation $ x=k $, where k is a constant indicating the line's position along the x-axis. For a line passing through the origin, this constant is zero, k=0. Hence, the equation of the line becomes $ x = 0 $.

Other special cases of lines passing through the origin occur when the slope is either m=1 or m=-1.

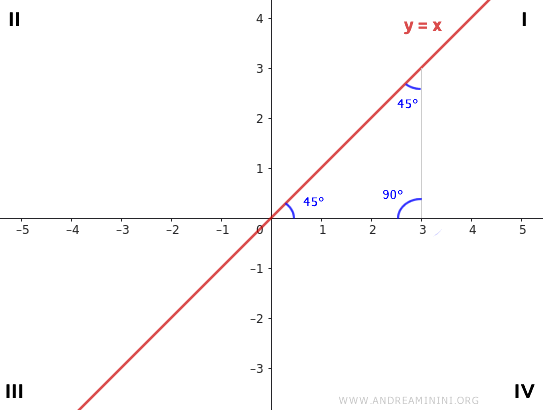
If m=1, the line coincides with the bisector of the first and third quadrants. In this case, the equation of the line is $ y = x $
If m=-1, the line coincides with the bisector of the second and fourth quadrants. In this case, the equation of the line is $ y = -x $

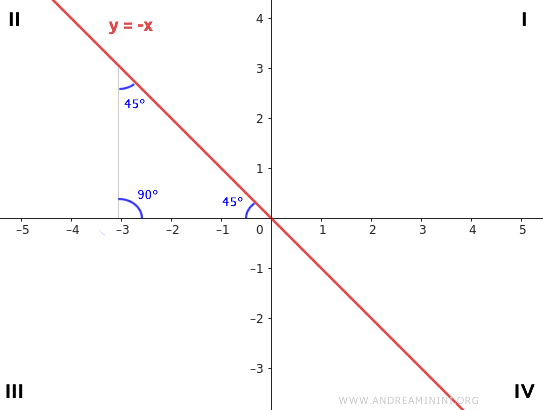
In both cases, where m=1 and m=-1, a right isosceles triangle is formed, with one angle being 90° and the adjacent angles being 45° each.

And so forth.