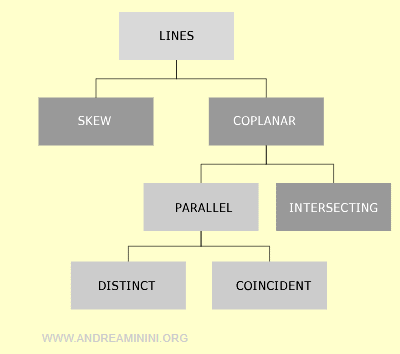
Coplanar, Skew, Parallel, or Intersecting Lines in Space
In space, two lines can be coplanar or skew depending on whether they lie in the same plane or not. Coplanar lines can further be categorized as parallel (distinct or coincident) or intersecting.
The Position of Lines in Space
In three-dimensional space (x, y, z), lines can either be skew or coplanar, depending on their positions.
- Coplanar Lines
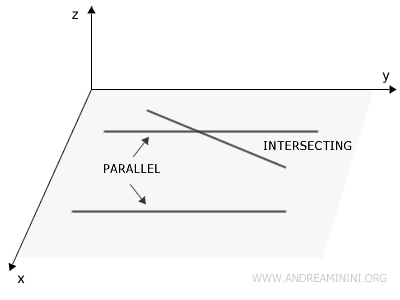
Two lines are coplanar if they lie in the same plane. Coplanar lines can be intersecting if they share a common point, coincident if they share all points, or parallel if they share no points.
- Skew Lines
Two lines are skew if they do not lie in the same plane. In this case, the lines are in different planes, do not intersect, and are not parallel.
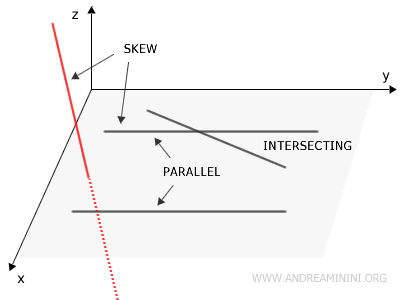
The unique feature of skew lines is that no single plane contains both lines. Therefore, skew lines differ from parallel lines, which do not intersect but lie in the same plane. To visualize skew lines, think of two pencils held in the air so that they neither touch nor are parallel.
How to Determine if Two Lines are Coplanar
To determine if two lines are coplanar, we can use linear algebra.
The process differs depending on whether the line equations are in Cartesian or vector/parametric form.
A] Cartesian Equations
Using Cartesian equations, a line can be represented as the intersection of planes.
$$ \begin{cases} a_1 x + b_1 y + c_1 z + d_1 = 0 \\ a_2 x + b_2 y + c_2 z + d_2 = 0 \end{cases} $$
$$ \begin{cases} a_3 x + b_3 y + c_3 z + d_3 = 0 \\ a_4 x + b_4 y + c_4 z + d_4 = 0 \end{cases} $$
We write the equations as a system:
$$ \begin{cases} a_1 x + b_1 y + c_1 z + d_1 = 0 \\ a_2 x + b_2 y + c_2 z + d_2 = 0 \\ a_3 x + b_3 y + c_3 z + d_3 = 0 \\ a_4 x + b_4 y + c_4 z + d_4 = 0 \end{cases} $$
or
$$ \begin{cases} a_1 x + b_1 y + c_1 z = - d_1 \\ a_2 x + b_2 y + c_2 z = - d_2 \\ a_3 x + b_3 y + c_3 z = - d_3 \\ a_4 x + b_4 y + c_4 z = - d_4 \end{cases} $$
This system has three variables (x, y, z).
The coefficient matrix of the system is:
$$ A = \begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \\ a_4 & b_4 & c_4 \end{pmatrix} $$
The augmented matrix of the system is:
$$ A|B = \begin{pmatrix} a_1 & b_1 & c_1 & -d_1 \\ a_2 & b_2 & c_2 & -d_2 \\ a_3 & b_3 & c_3 & -d_3 \\ a_4 & b_4 & c_4 & -d_4 \end{pmatrix} $$
According to the Rouché-Capelli theorem, the system has solutions if the rank of A equals the rank of A|B. In this case, the lines are either coplanar intersecting or coincident.
- If the rank (r) equals the number of variables (n=3), then the system has a unique solution. Thus, the lines are intersecting.
$$ rg(A) = rg(A|B) = 3 $$ - If the rank (r) is less than the number of variables (n=3), then the system has infinitely many solutions (∞n-r). Thus, the lines are coincident.
$$ rg(A) = rg(A|B) < 3 $$
If the rank of A differs from the rank of A|B, the system has no solutions. In this case, the lines are either skew or coplanar parallel.
- If the rank (r) of A|B equals 4, then the direction vectors of the lines are linearly independent. Thus, the lines are skew.
$$ rg(A) ≠ rg(A|B) = 4 $$ - If the rank (r) of A|B is less than 4, then the direction vectors of the lines are linearly dependent. Thus, the lines are parallel and coplanar.
$$ rg(A) ≠ rg(A|B) < 4 $$
Example
Consider the Cartesian equations of two lines in space:
$$ \begin{cases} 4x+3y+2z=4 \\ -3x+2y+z=4 \end{cases} $$
$$ \begin{cases} 3x-4y-2z=2 \\ -3x-3y+2z=1 \end{cases} $$
We combine them into a single linear system:
$$ \begin{cases} 4x+3y+2z=4 \\ -3x+2y+z=4 \\ 3x-4y-2z=2 \\ -3x-3y+2z=1 \end{cases} $$
Next, we calculate the rank of the coefficient matrix A:
$$ r_A = \begin{pmatrix} 4 & 3 & 2 \\ -3 & 2 & 1 \\ 3 & -4 & -2 \\ -3 & -3 & 2 \end{pmatrix} = 3 $$
and the rank of the augmented matrix A|B:
$$ r_{A|B} = \begin{pmatrix} 4 & 3 & 2 & 4 \\ -3 & 2 & 1 & 4 \\ 3 & -4 & -2 & 2 \\ -3 & -3 & 2 & 1 \end{pmatrix} = 4 $$
The rank of A does not match the rank of A|B.
Thus, the system has no solutions.
The two lines are skew because the rank of A|B is 4.
B] Vector or Parametric Equations
If the line equations are in vector/parametric form, we need to check if the direction vectors of the lines are linearly dependent or not.
$$ \begin{cases} x =x_1 + l_1t_1 \\ y=y_1 + m_1t_1 \\ z=z_1 + n_1t_1 \end{cases} $$
$$ \begin{cases} x=x_2 + l_2t_2 \\ y=y_2 + m_2t_2 \\ z=z_2 + n_2t_2 \end{cases} $$
We form a matrix with the direction vectors.
Then we calculate the rank of the matrix.
$$ r_k = \begin{pmatrix} l_1 & l_2 \\ m_1 & m_2 \\ n_1 & n_2 \end{pmatrix} $$
If the rank is:
- rk = 1. The direction vectors are linearly dependent. Thus, the two lines are either parallel and distinct or coincident. They are always coplanar.
- If they have infinitely many points in common, they are coincident.
- If they have no points in common, they are parallel.
- rk = 2. The direction vectors are linearly independent. In this case, the lines could be coplanar and intersecting or skew.
- If they have one point in common, they are coplanar and intersecting.
- If they have no points in common, they are skew.
Example
Consider the parametric equations of two lines in space:
$$ \begin{cases} x=3 + 2t_1 \\ y=-1 + 3t_1 \\ z=1 + 4t_1 \end{cases} $$
$$ \begin{cases} x=1 + 3t_2 \\ y=2 + t_2 \\ z=4 -2t_2 \end{cases} $$
The direction vectors of the two lines are:
$$ v_1 = \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} $$
$$ v_2 = \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} $$
We form a matrix with the direction vectors as columns.
$$ \begin{pmatrix} 2 & 3 \\ 3 & 1 \\ 4 & -2 \end{pmatrix} $$
Then we calculate the rank of the matrix:
$$ r_k = \begin{pmatrix} 2 & 3 \\ 3 & 1 \\ 4 & -2 \end{pmatrix} = 2 $$
The rank is 2.
The vectors are linearly independent.
At this point, the lines could be either skew or coplanar and intersecting.
We verify if they have any points in common.
$$ \begin{cases} x=3 + 2t_1 \\ y=-1 + 3t_1 \\ z=1 + 4t_1 \\ x=1 + 3t_2 \\ y=2 + t_2 \\ z=4 -2t_2 \end{cases} $$
$$ \begin{cases} 1 + 3t_2 = 3 + 2t_1 \\ 2 + t_2 = -1 + 3t_1 \\ 4 - 2t_2 = 1 + 4t_1 \end{cases} $$
$$ \begin{cases} t_2 = \frac{2 + 2t_1}{3} \\ 2 + \frac{2 + 2t_1}{3} = -1 + 3t_1 \\ 4 - 2t_2 = 1 + 4t_1 \end{cases} $$
$$ \begin{cases} t_2 = \frac{2 + 2t_1}{3} \\ t_1 = \frac{11}{7} \\ 4 - 2t_2 = 1 + 4t_1 \end{cases} $$
$$ \begin{cases} t_2 = \frac{2 + 2(\frac{11}{7})}{3} \\ t_1 = \frac{11}{7} \\ 4 - 2t_2 = 1 + 4t_1 \end{cases} $$
$$ \begin{cases} t_2 = \frac{12}{7} \\ t_1 = \frac{11}{7} \\ \frac{4}{7} = \frac{51}{7} \end{cases} $$
The system has no solution. The two lines do not have any points in common. They are not intersecting.
Therefore, the two lines are skew.
And so on.
