Linear Systems

A linear system is composed of two or more linear equations.

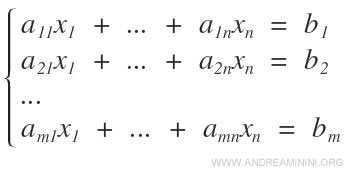
To solve a linear system, one must find solutions that simultaneously satisfy all the linear equations in the system.

Characteristics of a Linear System

A linear system consists of m equations and n unknowns. Both the coefficients a_ij and the constant terms b_ij are real numbers.

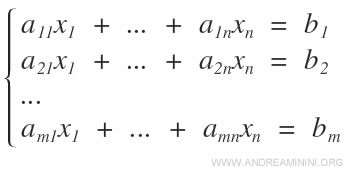
There is no direct correlation between the number of rows m and the number of equations n.

The Case of a Square Linear System. When the number of rows and columns is equal, the linear system is referred to as square.

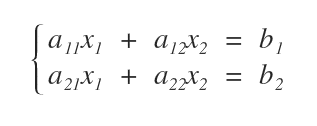
Indices of the System

The ij indices follow a row, column order.

1. Index i represents the equation. Thus, index i varies from 1 to the number of equations m.
2. Index j represents the unknown variable. Hence, index j ranges from 1 to the number of unknowns n in the equation.

Solutions of the Linear System

A solution to a linear system is an ordered n-tuple of real numbers (s₁, ..., s_n) that, when substituted sequentially for the n unknowns x₁ ... x_n, simultaneously satisfies all the equations in the system.

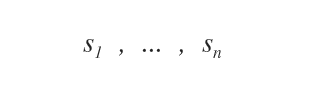
A linear system may have more than one solution or none at all.

The set S represents the collection of all solutions to the linear system.

The Solution Set

The solution set of a linear system is described as:

• Compatible, if at least one solution exists.
• Incompatible or impossible, if no solution exists. The solution set of a linear system is determined by the intersection of the solution sets of the individual equations.

An Example of a Linear System with a Single Solution

This linear system has only one solution because the two lines intersect at a single point.

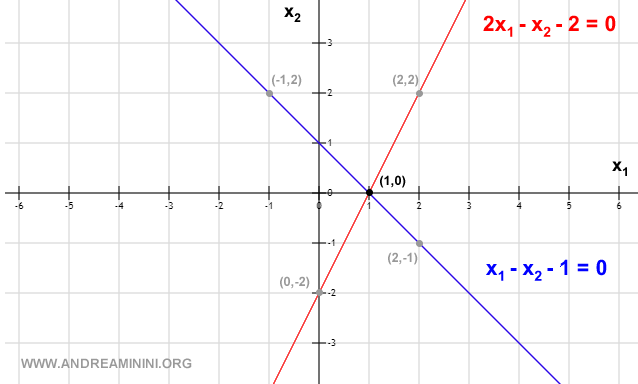
The intersection of the two lines on the plane represents the solution of the system.

The point where the two intersecting lines meet identifies the values of the two unknowns (x₁, x₂) that solve the linear system.

An Example of a Linear System with No Solution

The following system, however, has no solution as the two lines never intersect. They are parallel lines.

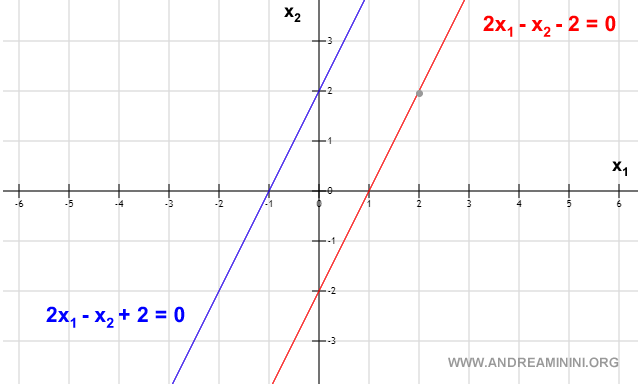
In this case, the lines are parallel, and the solution set is an empty set ( S=Ø ).

An Example of a Linear System with Infinite Solutions

In the following linear system, the two lines are coincident.

This is a case of a linear system with infinite solutions.

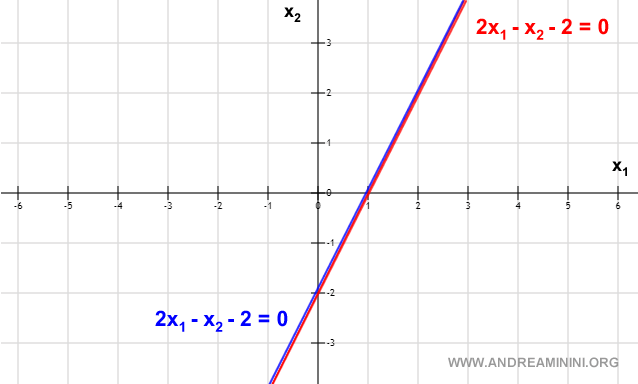
The solution set of the linear system is infinite because the countless points of the first line coincide with those of the second.