Concurrente Pencil of Lines
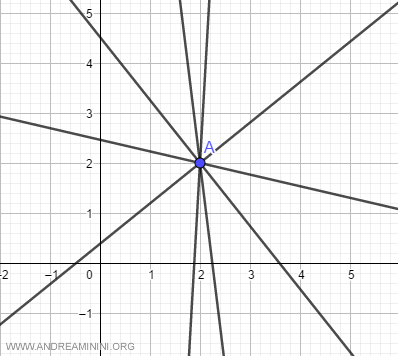
A concurrent pencil of lines is a set of all lines that converge at a specific point (A) on the plane, known as the center of the pencil.
The equation of the pencil of lines centered at a point with coordinates \((x_0, y_0)\) is given by:
$$ y-y_0 = m \cdot (x-x_0) $$
This equation describes all the lines in the pencil that pass through the point \( (x_0, y_0) \), as the slope \( m \in \mathbb{R} \) varies, except for the line parallel to the y-axis.
Note. The line parallel to the y-axis cannot be expressed with the explicit form \( y = mx \) because there is no value of \( m \) that can represent it. For lines parallel to the y-axis, use the equation: $$ x = x_0 $$
In general, given a point P with coordinates $ (x_0, y_0) $, the pencil of lines centered at P has the following equations:
$$
\begin{cases}
y - y_0 = m \cdot (x - x_0) & \text{if the line is not parallel to the y-axis} \\
x = x_0 & \text{if the line is parallel to the y-axis}
\end{cases}
$$
The set of all lines converging at the center of the pencil is called a complete pencil.
Alternatively, I can represent the lines of the pencil centered at C using this form: $$ y-y_0 = -\frac{h}{k} \cdot (x-x_0) $$ where h and k are any integers $ h,k \in \mathbb{Z} $ with k≠0.
A Practical Example
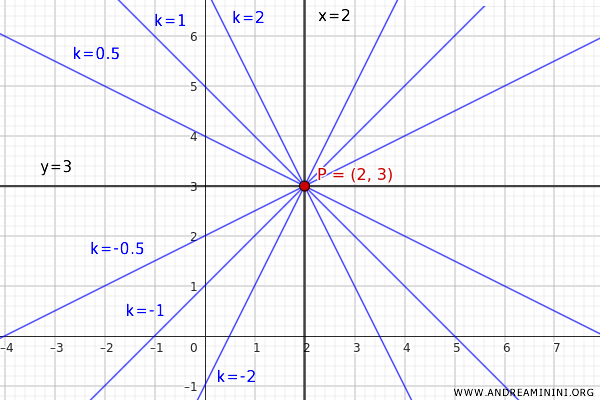
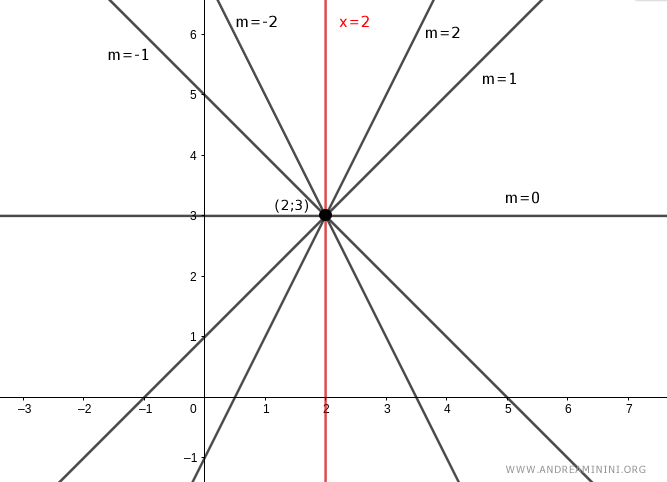
Let's consider a point on the plane P(2,3) as the center of the pencil.
Then we use the equations for the pencil of lines.
$$
\begin{cases}
y - y_0 = m \cdot (x - x_0) \\
x = x_0
\end{cases}
$$
In this case, the coordinates of the center of the pencil are P(2,3), with x0=2 and y0=3
$$
\begin{cases}
y - 3 = m \cdot (x - 2) \\
x = 2
\end{cases}
$$
The equation \( y - 3 = m(x - 2) \) represents a pencil of lines passing through the point \( (2, 3) \). This pencil includes all possible lines with various slopes \( m \), except for those parallel to the y-axis.
The equation \( x = 2 \), shown as a red line, represents the line parallel to the y-axis passing through the point \( (2, 3) \).
Here are some lines from the complete pencil centered at P(2,3).
Example 2
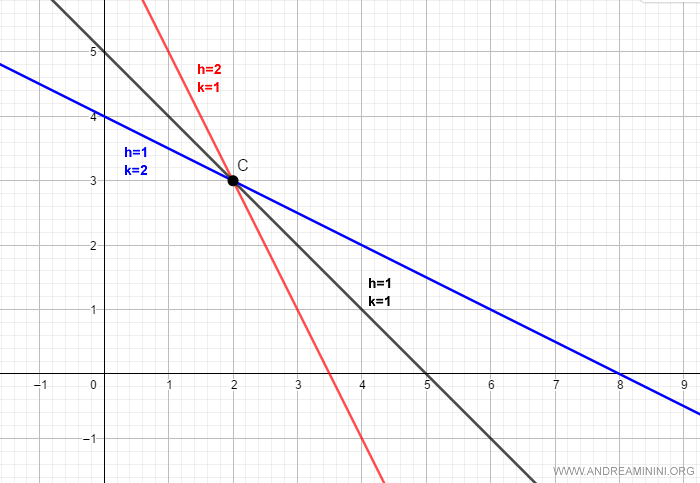
In this example, let's consider a point C
$$ C = \begin{pmatrix} x_0 = 2 \\ y_0 = 3 \end{pmatrix} $$
We can represent the lines of the pencil centered at C using this equation:
$$ y-y_0 = -\frac{h}{k} \cdot (x-x_0) $$
where h and k are any integers $ h,k \in \mathbb{Z} $ with k≠0 to avoid the problem of division by zero.
$$ y-3 = -\frac{h}{k} \cdot (x-2) $$
Then, solving for y, we get the explicit form of the line equation.
$$ y = -\frac{h}{k} \cdot (x-2) + 3 $$
For every combination of h and k, there is a line passing through the point C.
Thus, to obtain the complete pencil of lines, we simply vary the ratio h/k.
In this case as well, the line parallel to the y-axis must be represented with a separate equation, which is $ x=x_0 $, in this case, $ x = 2 $.
The Proof
A pencil of lines has its center at point P with coordinates (x0;y0)
$$ P(x_0;y_0) $$
A general line in the pencil must pass through the point P(x0;y0)
$$ y = mx +q $$
Substitute y=y0 and x=x0
$$ y_0 = mx_0 +q $$
Then, solve for q
$$ q = y_0 -mx_0 $$
Substitute q=y0-mx0 back into the general line equation.
$$ y = mx +q $$
$$ y = mx + (y_0 -mx_0) $$
$$ y = mx + y_0 -mx_0 $$
Separate the variables y and x on both sides of the equation
$$ y - y_0 = mx -mx_0 $$
$$ y - y_0 = m (x -x_0) $$
The final result is the equation of the pencil of lines.
Note. This equation represents all the lines in the pencil except the line parallel to the y-axis. For that line, we must use the specific equation x=x0.
Alternative Proof
If the point A on the plane has the following coordinates
$$ A = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} $$
then the Cartesian equation of all the lines in the pencil is
$$ h(x-x_0) + k(y-y_0) = 0 $$
where h and k are coefficients that we don't know yet.
Divide both sides of the equation by k.
$$ \frac{h(x-x_0)}{k} + \frac{k(y-y_0)}{k} = 0 $$
$$ \frac{h(x-x_0)}{k} + y-y_0 = 0 $$
Then, separate the variables y and x on both sides of the equation
$$ y-y_0 = -\frac{h}{k} \cdot (x-x_0) $$
The ratio -h/k is the slope (m) of the lines.
Replace it with m and rewrite the equation of the pencil of lines in explicit form.
$$ y-y_0 = m \cdot (x-x_0) $$
Every line in the pencil is identified by a particular value of the slope m.
Note. In the special case where the line is parallel to the y-axis, meaning it is vertical, the equation does not work because m is undefined. In this case , the equation of the line is x-x0=0.
Generating Lines of the Pencil
To generate a pencil of lines, I can choose two intersecting lines r and s, called the generating lines of the pencil.
$$ ax+by+c=0 $$
$$ a'x+b'y+c'=0 $$
The pencil of lines is generated by considering every possible linear combination of these two lines:
$$ p \cdot (ax+by+c) + q ( a'x+b'y+c') = 0 $$
where p and q are scalars.
To obtain a more compact equivalent form, divide both sides of the equation by p.
$$ \require{cancel} \frac{ \cancel{p}\cdot (ax+by+c)}{ \cancel{p}} + \frac{q ( a'x+b'y+c')}{p} = \frac{0}{p} $$
$$ ax+by+c + \frac{q}{p} \cdot ( a'x+b'y+c') = 0 $$
Assume p is always non-zero p≠0 to avoid the problem of division by zero.
Introduce the parameter $ k = \frac{q}{p} $ for further simplification:
$$ ax+by+c + k \cdot ( a'x+b'y+c') = 0 $$
where k is any rational number and each value of k corresponds to a line in the pencil.
This equation represents all the lines in the pencil except the line $ a'x+b'y+c'=0 $, which cannot be obtained in this form because it would require k to approach infinity.
Note. The line $ ax+by+c=0 $ can be generated by setting k=0 or q/p=0. Conversely, the line $ a'x+b'y+c'=0 $ cannot be generated in the form $$ (ax+by+c) + k \cdot ( a'x+b'y+c') = 0 $$ It can only be approximated by making k tend to infinity $ k \rightarrow \infty $. The only way to obtain the line $ a'x+b'y+c'=0 $ is to go back to the initial linear combination by assigning the values p=0 and q=1 to the coefficients $$ p \cdot (ax+by+c) + q ( a'x+b'y+c') = 0 $$
Which Generating Lines to Choose for Constructing a Pencil Centered at P(x0;y0)?
Any intersecting lines passing through the point P(x0;y0) will work.
However, to simplify calculations, it is better to choose those parallel to the Cartesian axes that pass through P(x0;y0).
$$ y = y_0 $$
$$ x = x_0 $$
which are the equations of the lines
$$ y - y_0 = 0 $$
$$ x - x_0 = 0 $$
In this way, the equation of the pencil becomes
$$ p \cdot ( y-y_0 ) + q ( x-x_0 ) = 0 $$
$$ (y -y_0) + \frac{q}{p} \cdot ( x-x_0) = 0 $$
Note. The final result is equivalent to the formula for the equation of a line passing through a point with a slope $ m= - \frac{q}{p} $. $$ y = m \cdot ( x-x_0) + y_0 $$
Which Line in the Pencil Passes Through the Origin?
To find the value of \( k \) that generates a line passing through the origin O(0;0) of the Cartesian axes, consider the pencil equation
$$ (ax+by+c) + k \cdot (a'x+b'y+c') = 0 $$
The line we want must pass through the points x=0 and y=0.
So, substitute these values into the pencil equation:
$$ a \cdot 0 + b \cdot 0 + c + k \cdot (a' \cdot 0 + b' \cdot 0 + c') = 0 $$
$$ c + k \cdot c' = 0 $$
Finally, solve for k
$$ k \cdot c' = -c $$
$$ k = -\frac{c}{c'} $$
This is the value of \( k \) that generates a line in the pencil passing through the origin, provided that \( c' \neq 0 \) to avoid division by zero.
Note. If \( c' = 0 \) and \( c \neq 0 \), there is no finite value of \( k \) for which the line passes through the origin. If both \( c \) and \( c' \) are zero, any value of \( k \) satisfies the equation, indicating that all lines in the pencil pass through the origin.
Example
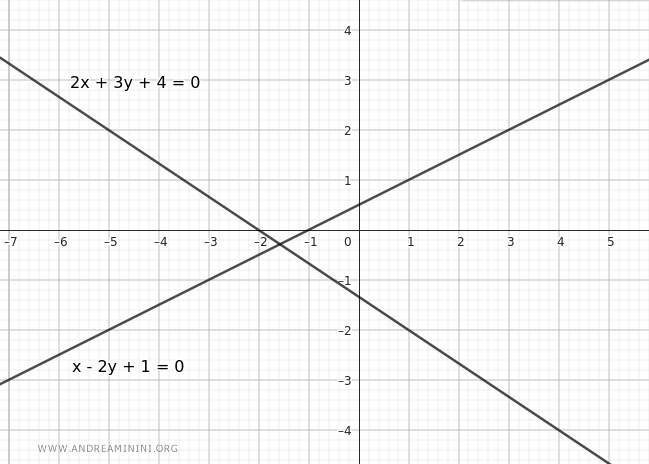
Consider two generating lines in the Cartesian plane, defined by the following equations:
$$ r: \ 2x + 3y + 4 = 0 $$
$$ s: \ x - 2y + 1 = 0 $$
Being two intersecting lines, we can choose them as generating lines for the pencil.
We use their linear combination to express the pencil:
$$ (2x + 3y + 4) + k \cdot (x - 2y + 1) = 0 $$
Expand and collect like terms:
$$ (2 + k)x + (3 - 2k)y + (4 + k) = 0 $$
This equation generates the lines in the pencil as the parameter k varies, except for the line $ s: \ x - 2y + 1 = 0 $.
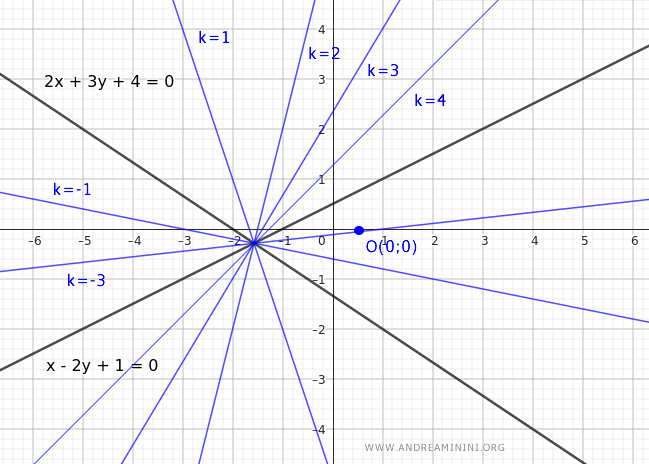
Note. The line $ s: x-2y+1=0 $ must be added separately to the pencil because it does not correspond to any value of k.
What is the Equation of the Line that Passes Through the Origin?
To find the line in the pencil that passes through the origin, impose that the equation is satisfied for \( x = 0 \) and \( y = 0 \):
$$ (2 + k) x + (3 - 2k)y + (4 + k) = 0 $$
$$ (2 + k) \cdot 0 + (3 - 2k) \cdot 0 + (4 + k) = 0 $$
$$ 4 + k = 0 $$
Solve for k and get k=-4
$$ k = -4 $$
Substitute k=-4 into the pencil equation to get the equation of the line passing through the origin:
$$ (2 - 4)x + (3 + 8)y + (4 - 4) = 0 $$
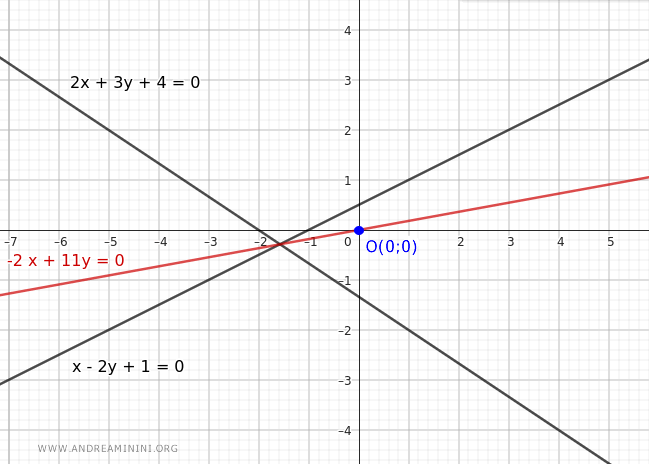
$$ -2x + 11y = 0 $$
$$ y = \frac{2}{11}x $$
This is the equation of the line in our pencil that passes through the origin.
Example 2
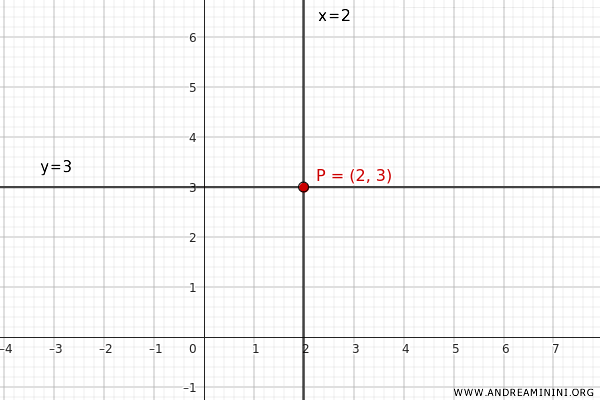
In this example, I want to construct a pencil of lines centered at a specific point, such as P(2;3).
$$ P (2;3 ) $$
First, I choose two intersecting lines passing through point P to use as generating lines for the pencil.
We can choose from infinite lines... but it is much simpler to use the lines parallel to the axes as generating lines:
- A line parallel to the x-axis and passing through \( (2,3) \), with the equation \( y = 3 \) or $ y - 3 = 0 $.
- A line parallel to the y-axis and passing through \( (2,3) \), with the equation \( x = 2 \) or $ x - 2 = 0 $.
These two lines intersect at point P(2;3).
Substitute the two equations $ y-3=0 $ and $ x-2=0 $ into the pencil equation.
$$ (ax+by+c) + k \cdot (a'x+b'y+c') = 0 $$
$$ (y-3) + k \cdot (x-2) = 0 $$
$$ y = - k \cdot (x-2) +3 $$
$$ y = - kx + 2k +3 $$
where k is the slope that varies, generating infinite lines that all pass through point P(2,3).
Each value of k determines a different line in the pencil.