Orthogonal Projections
Orthogonal projection of a point P onto a line r is the foot of the perpendicular from the point to the line.
For instance, consider a point P and a line r.
The orthogonal projection is the point P', where the perpendicular from point P intersects the line r.
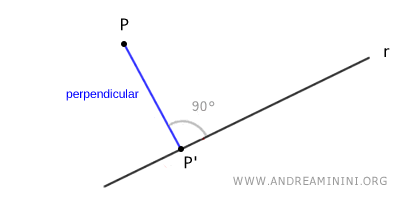
Thus, in this example, the orthogonal projection is the point P' on the line r.
The segment PP′, which connects P to its projection on r, is the shortest possible path from P to any point on the line.
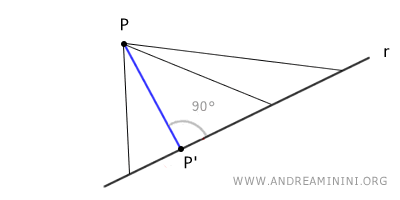
Through point P, there is exactly one line that is perpendicular to a given line. Therefore, it is possible to draw only one line perpendicular to line r that passes through point P.
A perpendicular is a line or segment that passes through a point P and intersects line r at a right angle (90°). In a plane, it is the shortest segment connecting point P to a point on the line.
Proof
To prove both the existence and uniqueness of the perpendicular from a point P to a line r, consider two distinct points A and B that are equidistant from the foot of the perpendicular, so that $ AP' \cong BP' $.
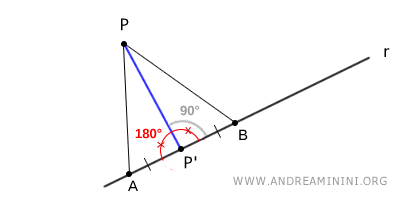
The perpendicular intersects line $ r $ at a 90° angle and bisects the straight angle $ A\hat{P'} B = 180^\circ $.
Since a straight angle has only one bisector, the perpendicular from P to line $ r $ must also be unique.
Projection of a Segment
The orthogonal projection of a segment follows a similar process.
For example, consider a segment AB and a line r.
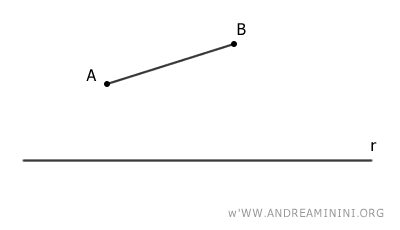
Project the endpoints A and B of the segment onto the line and connect them.
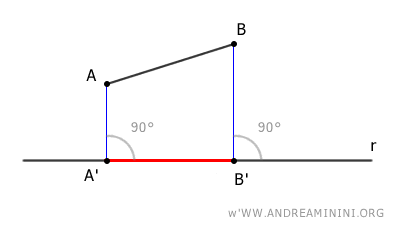
Therefore, the orthogonal projection of segment AB onto line r is the segment A'B'.
Note: The orthogonal projection A'B' of a segment onto a line is congruent to the original segment AB only when the segment is parallel to the line.
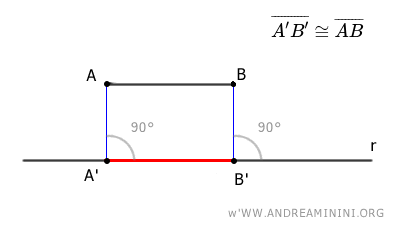
In all other cases, the length of the orthogonal projection is always shorter than that of the original segment. $$ \overline{A'B'} \le \overline{AB} $$ In the special case where the original segment is perpendicular to the line, the orthogonal projection reduces to a single point.
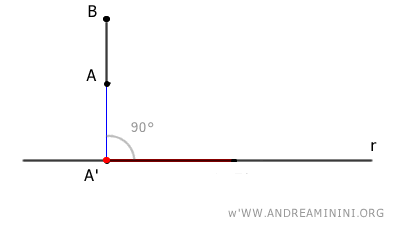
And so forth.
