Distance Between Two Skew Lines
The distance between two skew lines $ r $ and $ s $ is the length of the common perpendicular segment $ AB $, which is the shortest segment connecting a point on one line to a point on the other. $$ AB \perp r $$ $$ AB \perp s $$ Here, $ A \in r $ and $ B \in s $.
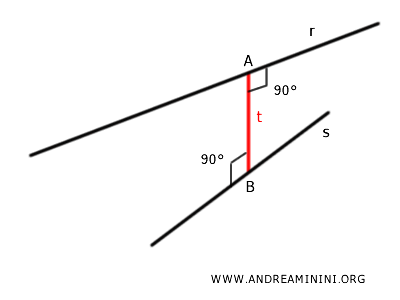
There is a unique line $ t $ that is perpendicular to both skew lines $ r $ and $ s $.
This line $ t $ intersects each of the two lines at a point, $ A \in r $ and $ B \in s $, and the segment $ AB $ connecting these points represents the shortest distance between the lines.
Thus, the segment $ AB $ defines the distance between the two skew lines $ r $ and $ s $.
Note. In three-dimensional space (x, y, z), two lines are considered skew if they neither intersect nor are parallel.
The Proof
By definition, there is a unique line perpendicular to both skew lines. This line intersects each of the lines at a single point, and the segment joining these two points represents the shortest distance. Let’s demonstrate this.
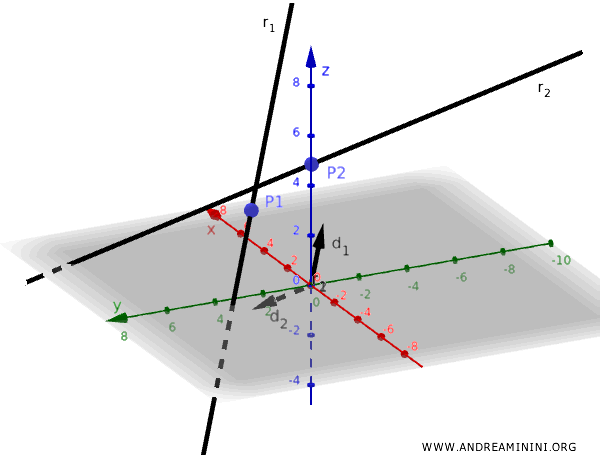
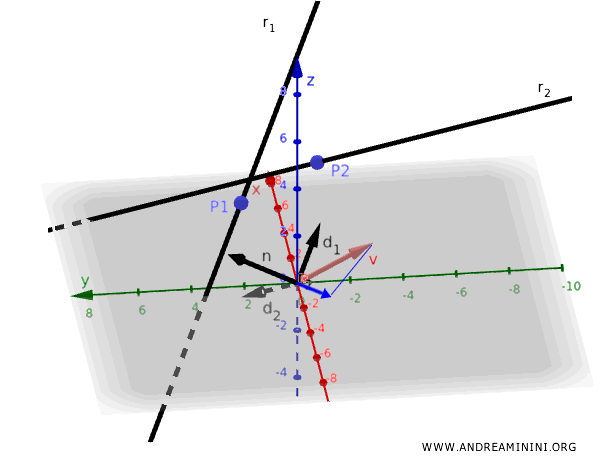
Consider two skew lines in three-dimensional space.
Since the lines are skew, they neither intersect nor are parallel.
- The first line \( r_1 \) passes through the point \( \mathbf{P}_1 \) and has a direction vector \( \mathbf{d}_1 \).
- The second line \( r_2 \) passes through the point \( \mathbf{P}_2 \) and has a direction vector \( \mathbf{d}_2 \).
The parametric equations of the lines are:
$$ r_1(t) = \mathbf{P}_1 + t \, \mathbf{d}_1 \quad \text{and} \quad r_2(s) = \mathbf{P}_2 + s \, \mathbf{d}_2 $$
Where \( t \) and \( s \) are real parameters.
To find a line perpendicular to both \( r_1 \) and \( r_2 \), two conditions must be satisfied:
- The line must be orthogonal to the direction vector \( \mathbf{d}_1 \) of \( r_1 \).
- The line must also be orthogonal to the direction vector \( \mathbf{d}_2 \) of \( r_2 \).
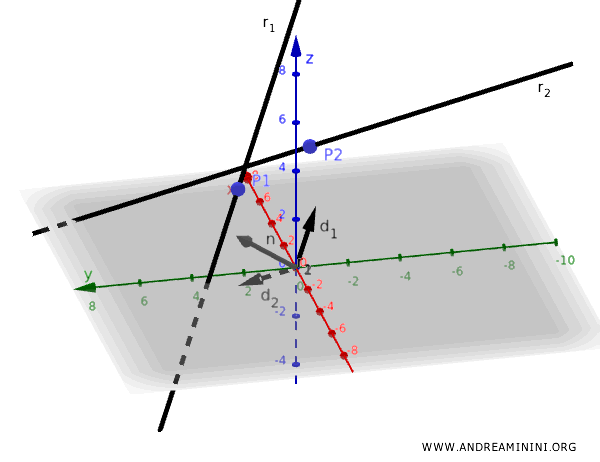
A vector \( \mathbf{n} \) orthogonal to both can be obtained by calculating the cross product:
$$ \mathbf{n} = \mathbf{d}_1 \times \mathbf{d}_2 $$
This vector \( \mathbf{n} \) serves as the direction vector for the required perpendicular line.
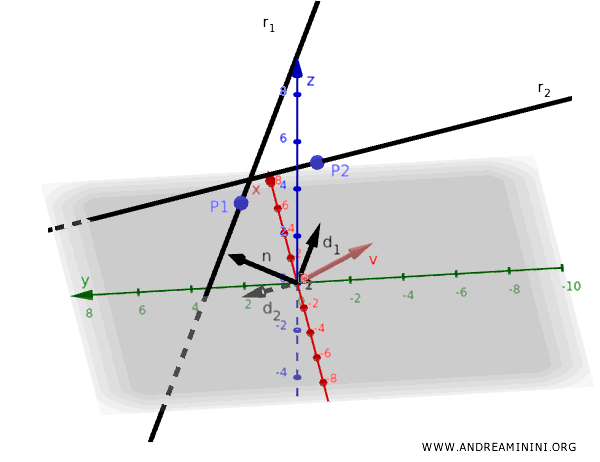
Next, consider a vector \( \mathbf{v} \) that connects a point on \( r_1 \) to a point on \( r_2 \):
$$ \mathbf{v} = \mathbf{P}_2 - \mathbf{P}_1 $$
The shortest distance is determined by projecting \( \mathbf{v} \) onto \( \mathbf{n} \):
$$ d = \frac{| \mathbf{v} \cdot \mathbf{n} |}{\|\mathbf{n}\|} $$
Where \( \mathbf{v} \cdot \mathbf{n} \) is the dot product of \( \mathbf{v} \) and \( \mathbf{n} \), and \( \|\mathbf{n}\| \) is the magnitude of \( \mathbf{n} \).
The perpendicular line is unique because the vector \( \mathbf{n} \), derived as \( \mathbf{d}_1 \times \mathbf{d}_2 \), is itself unique.
Therefore, the points where this line intersects \( r_1 \) and \( r_2 \) are uniquely determined, ensuring that the shortest segment is also unique.
A Practical Example
Let’s consider two skew lines in space with the following parametric equations:
The first line (\( r_1 \)):
$$ r_1: \begin{cases}
x = 1 + t \\
y = 2 - t \\
z = 3 + 2t
\end{cases} $$
Here, \( \mathbf{P}_1 = (1, 2, 3) \) is a point on \( r_1 \), and \( \mathbf{d}_1 = (1, -1, 2) \) is its direction vector.
The second line (\( r_2 \)):
$$ r_2: \begin{cases}
x = 2 + s \\
y = -1 + 2s \\
z = 4 - s
\end{cases} $$
Here, \( \mathbf{P}_2 = (2, -1, 4) \) is a point on \( r_2 \), and \( \mathbf{d}_2 = (1, 2, -1) \) is its direction vector.
We calculate a vector \( \mathbf{n} \), which is orthogonal to both direction vectors \( \mathbf{d}_1 \) and \( \mathbf{d}_2 \), by taking the cross product:
$$ \mathbf{n} = \mathbf{d}_1 \times \mathbf{d}_2 $$
Given the direction vectors \( \mathbf{d}_1 = (1, -1, 2) \) and \( \mathbf{d}_2 = (1, 2, -1) \):
$$ \mathbf{n} = \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
1 & -1 & 2 \\
1 & 2 & -1
\end{vmatrix}
= \mathbf{i} \begin{vmatrix} -1 & 2 \\ 2 & -1 \end{vmatrix}
- \mathbf{j} \begin{vmatrix} 1 & 2 \\ 1 & -1 \end{vmatrix}
+ \mathbf{k} \begin{vmatrix} 1 & -1 \\ 1 & 2 \end{vmatrix}
$$
$$ \mathbf{n} = \mathbf{i}((-1)(-1) - (2)(2)) - \mathbf{j}((1)(-1) - (1)(2)) + \mathbf{k}((1)(2) - (1)(-1)) $$
$$ \mathbf{n} = \mathbf{i}(1 - 4) - \mathbf{j}(-1 - 2) + \mathbf{k}(2 + 1) $$
$$ \mathbf{n} = -3\mathbf{i} + 3\mathbf{j} + 3\mathbf{k} $$
Therefore, the vector orthogonal to both direction vectors is:
$$ \mathbf{n} = (-3, 3, 3) $$
Next, we calculate a vector \( \mathbf{v} \) that connects the points \( \mathbf{P}_1 = (1, 2, 3) \) and \( \mathbf{P}_2 = (2, -1, 4) \):
$$ \mathbf{v} = \mathbf{P}_2 - \mathbf{P}_1 = (2 - 1, -1 - 2, 4 - 3) = (1, -3, 1) $$
The minimum distance between the lines is the projection of the vector \( \mathbf{v} \) onto \( \mathbf{n} \):
We compute the magnitude of the projection using the formula:
$$ d = \frac{| \mathbf{v} \cdot \mathbf{n} |}{\|\mathbf{n}\|} $$
First, calculate the dot product \( \mathbf{v} \cdot \mathbf{n} \):
$$ \mathbf{v} \cdot \mathbf{n} = (1)(-3) + (-3)(3) + (1)(3) = -3 - 9 + 3 = -9 $$
The absolute value of the dot product is:
$$ | \mathbf{v} \cdot \mathbf{n} | = |-9| = 9 $$
Now, compute \( \|\mathbf{n}\| \), the norm of \( \mathbf{n} \):
$$ \|\mathbf{n}\| = \sqrt{(-3)^2 + 3^2 + 3^2} = \sqrt{9 + 9 + 9} = \sqrt{27} = 3\sqrt{3} $$
Finally, the distance is:
$$ d = \frac{9}{3\sqrt{3}} = \frac{3}{\sqrt{3}} = \sqrt{3} $$
Therefore, the minimum distance between the two skew lines is:
$$ d = \sqrt{3} $$
This distance corresponds to the length of the common perpendicular segment $ AB $ between the two skew lines.
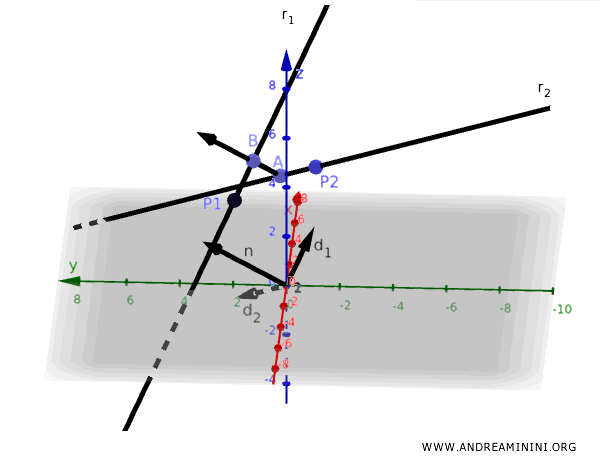
And that concludes the example.
