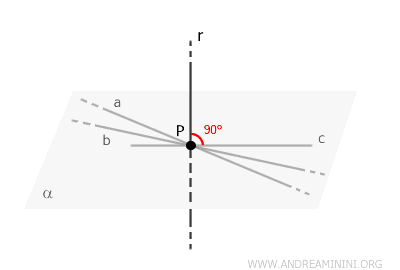
Line Perpendicular to a Plane

A line $r$ is perpendicular to a plane $\alpha$ if it intersects the plane and is perpendicular to every line that lies within the plane.

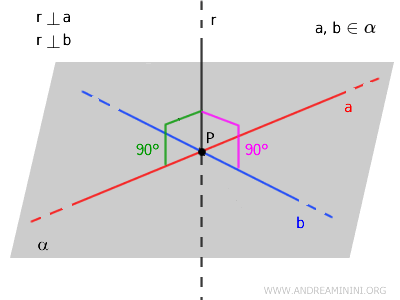
A line $r$ that is perpendicular to a plane $\alpha$ must meet two conditions:

• The line $r$ intersects the plane $\alpha$ at exactly one point $P$ within the plane.
• The line $r$ is perpendicular to all lines in the plane $\alpha$ that pass through the intersection point $P$.

Note: A line that intersects the plane at a single point but is not perpendicular is referred to as an oblique line to the plane.

Additional Remarks

Here are some further notes and observations regarding the perpendicularity of lines and planes.

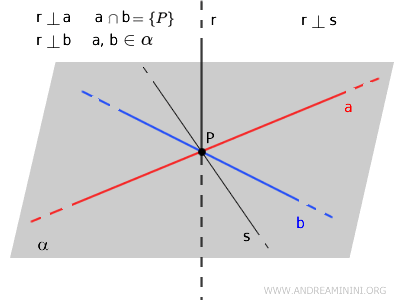
• Three Perpendicular Lines Theorem
  If two lines $a$ and $b$, both perpendicular to a line $r$, are drawn from a point $P$ on $r$, then $r$ is also perpendicular to any other line $s$ that passes through $P$ and lies in the plane $\alpha$ defined by $a$ and $b$.
  
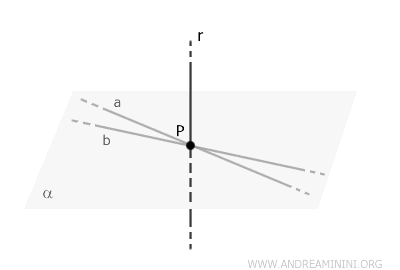
• Theorem of Perpendicular Lines to a Line in Space
  In space, any line perpendicular to a given line $r$ and passing through a point $P$ on $r$ must lie within the same plane.
  
• Theorem of the Three Perpendicular Lines
  Consider a line $r$ that is perpendicular to a plane $\alpha$. If a line $t$ is drawn from the foot of the perpendicular $H$, such that $t$ is perpendicular to another line $s$ lying in the plane $\alpha$, then $s$ is also perpendicular to the plane $\beta$, which is defined by lines $r$ and $t$.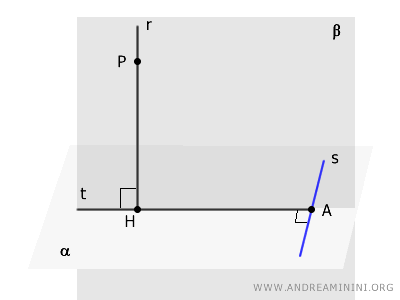

  

• Perpendicular Line to a Plane Theorem
  Through any point $P$ on the plane $\alpha$, there is exactly one line $r$ that is perpendicular to the plane.
  
• Perpendicular Lines Theorem
  Two lines that are perpendicular to the same plane are parallel to each other.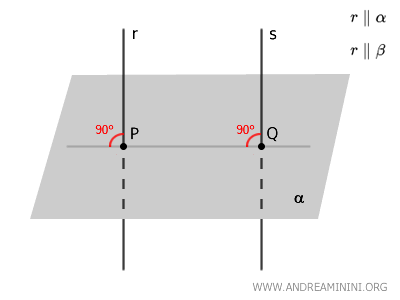

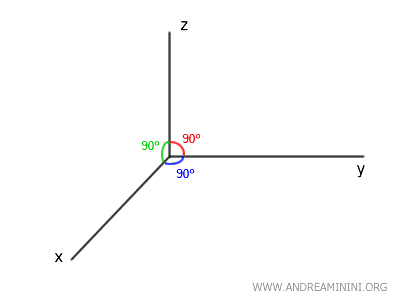
  Note. In three-dimensional space, the theorem stating that two lines perpendicular to the same line are parallel does not apply. This concept is valid only in a plane (2D). For example, the $x$, $y$, and $z$ axes in the Cartesian coordinate system are mutually perpendicular ($x \perp y$, $x \perp z$, $y \perp z$), yet they are not parallel to one another.
  

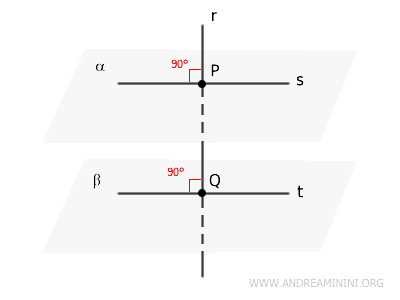
• Perpendicular Line Theorem for Two Planes
  If a line is perpendicular to two planes at two distinct points along its length, the two planes must be parallel.
  

And so on.