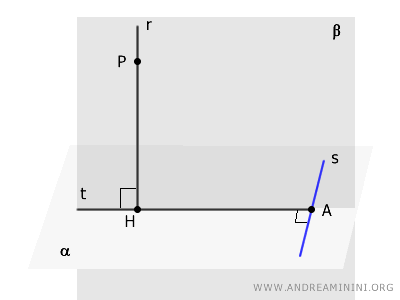
Theorem of the Three Perpendicular Lines

If from point $H$, where a line $r$ is perpendicular to a plane $ \alpha $, a line $t$ is drawn perpendicular to another line $s$ within the plane, then line $s$ is perpendicular to the plane $ \beta $ formed by lines $r$ and $t$.

The Proof

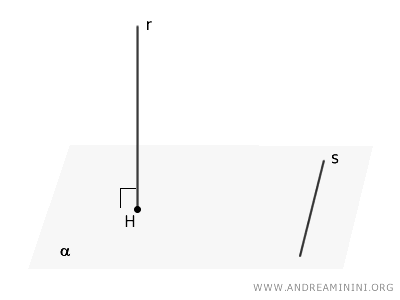
Let’s consider a plane $ \alpha $ and a line $r$ that is perpendicular to it ($ r \perp \alpha $), with $H$ being the foot of the perpendicular. Now, let $s$ be any line lying in plane $ \alpha $.

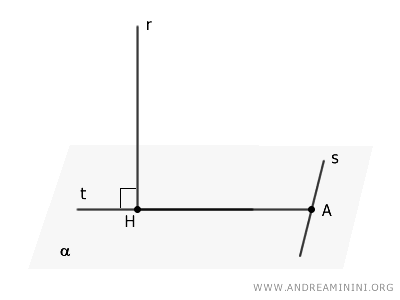
Draw a line $t$ perpendicular to $s$ that passes through point $H$, intersecting $s$ at point $A$.

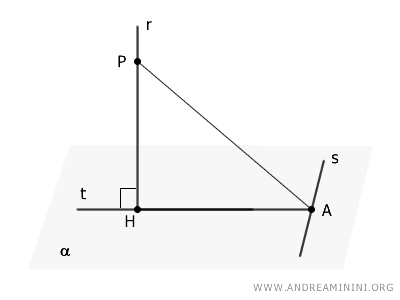
Next, select an arbitrary point $P$ on line $r$ and draw the segment $PA$.

Now, choose two points $B$ and $C$ on line $s$ such that they are equidistant from point $A$ but positioned on opposite sides of it.

This creates two congruent segments: $AB \cong AC$.

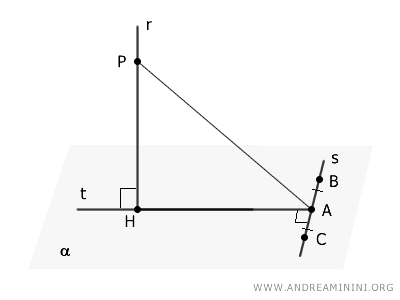
Next, connect points $B$ and $C$ to point $H$.

Since $H$ lies on the perpendicular bisector of segment $BC$, the triangle $BCH$ is isosceles, meaning its two oblique sides are congruent: $BH \cong CH$.

 

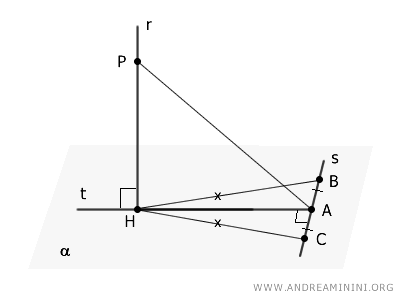
Then, connect points $B$ and $C$ to point $P$ on line $r$.

The triangles $BPH$ and $CPH$ are congruent because they share the side $HP$, have congruent sides $BH \cong CH$, and include the same angle (90°). Thus, the segments $BP \cong CP$ are congruent.

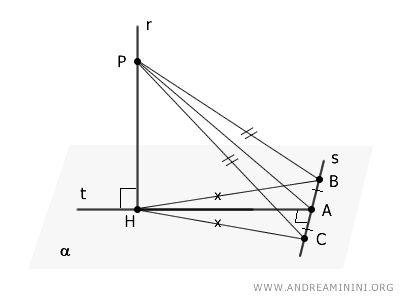
From this, we can conclude that triangle $BCP$ is isosceles since it has two equal sides: $BP \cong CP$.

As a result, the segment $AP$ acts as the median, perpendicular bisector, and altitude of the triangle. This implies that $AP$ is perpendicular to the base $BC$ of triangle $BCP$:

$$ AP \perp s $$

Finally, since $s$ is perpendicular to both $AH$ and $AP$, it follows that $s$ is also perpendicular to the plane $ \beta $ formed by the segments $AH$ and $AP$, which is the same as the plane defined by lines $r$ and $t$.

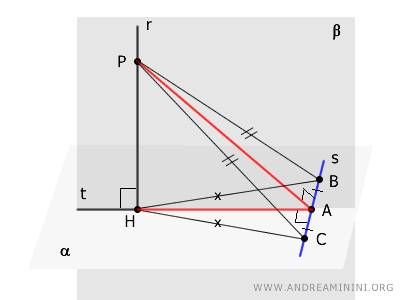
And that completes the proof.