Slope of a Line
The slope (or angular coefficient) of a line $$ y = mx + b $$ is the ratio of the difference in y-coordinates (yB - yA) to the difference in x-coordinates (xB - xA) for two distinct points on the line. $$ m = \frac{y_B - y_A}{x_B - x_A} $$ 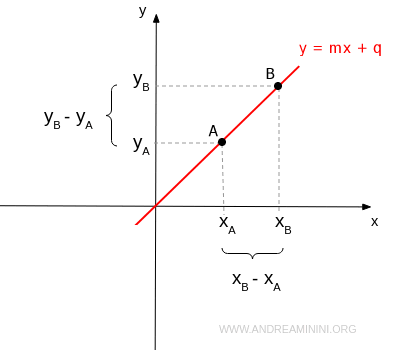
The slope measures the line's inclination (or steepness) relative to the x-axis.
It indicates the angle α between the line and the x-axis, with the vertex at their intersection and sides being the positive half of the x-axis and the line segment with a positive or zero y-coordinate.
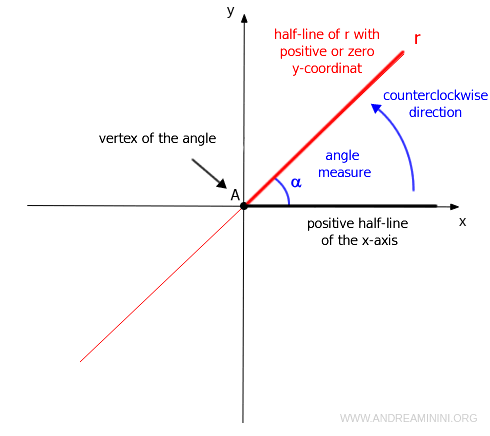
Note. By convention, the measure of an angle is taken counterclockwise from the positive x-axis.
The slope of a line can be positive, negative, or zero depending on the line's inclination.
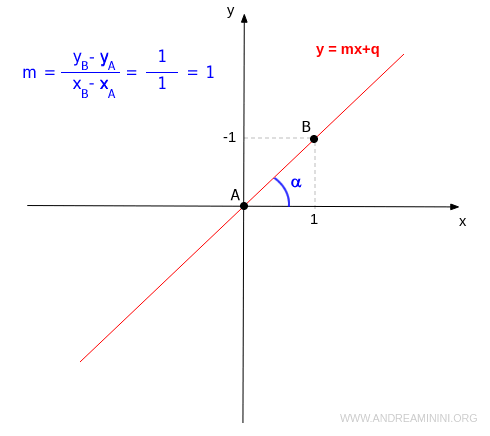
- If the slope is positive (m>0), the line is increasing. An acute angle forms between the line and the x-axis.
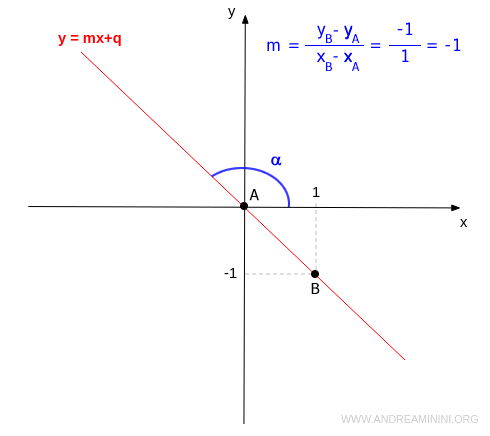
- If the slope is negative (m<0), the line is decreasing. An obtuse angle forms between the line and the x-axis.
- If the slope is zero (m=0), the line is constant. The line is parallel or coincident with the x-axis, creating no angle with the x-axis (or any other line parallel to the x-axis).
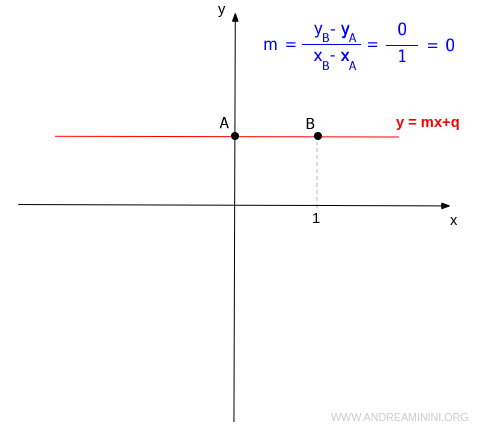
Note. The slope cannot be calculated for a vertical line, meaning it is parallel to the y-axis.
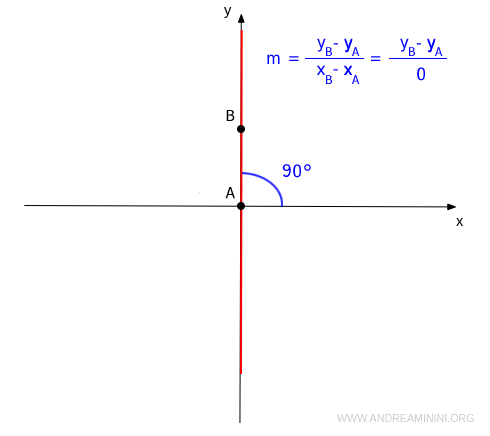
This occurs because when x=0 for any y, there is a division by zero in the slope calculation. $$ m = \frac{y_B - y_A}{x_B - x_A} = \frac{y_B - y_A}{0} $$ If, hypothetically, there was a quotient m from dividing by zero m=y/0, then y would need to equal m·0. However, this is impossible because zero is an absorbing element, and any number multiplied by zero is always zero y=m·0=0.
The Slope and the Tangent of the Angle
The slope m of a line is equal to the tangent of the angle α that the line forms with the x-axis. $$ m = \tan \alpha $$
This relationship allows me to describe the steepness of the line in trigonometric terms.
It is very useful for calculating the angle α given the slope of the line, and vice versa.
$$ m = \tan \alpha $$
$$ \alpha = \text{arctan} \ m $$
Where arctan is the arctangent, the inverse trigonometric function of the tangent.
Note. Understanding this formula requires knowledge of trigonometry and differential calculus. Therefore, it can only be fully understood starting from the fifth year of high school or the first year of university. The proof of this relationship is explained on another page of my notes, so I refer to that for further details and will not rewrite it here.
Example
The line y=2x-1 has a slope of m=2.
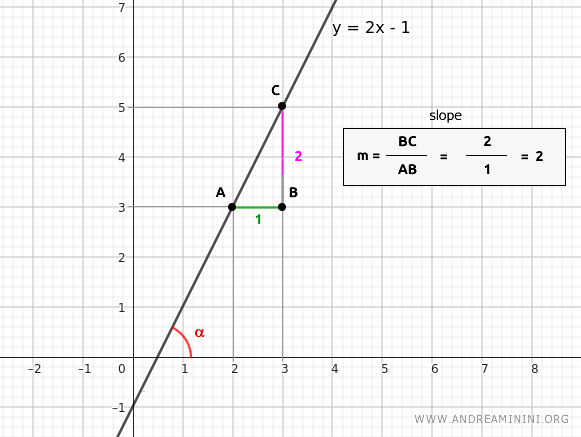
What is the angle α of the line?
To find the angle, we need to find a tangent value equal to the slope m=2.
$$ \tan \alpha = 2 $$
We calculate the arctangent (arctan) of both sides of the equation.
$$ \text{arctan}( \tan \alpha ) = \text{arctan} ( 2 ) $$
The arctangent is the inverse function of the tangent (tan), so they cancel each other out.
$$ \alpha = \text{arctan} ( 2 ) $$
Therefore, the angle α is equal to the arctangent of 2, which is approximately 1.107 radians.
$$ \alpha_{rad} = 1.107 \ rad $$
We convert the angle from radians to degrees using the formula $$ \alpha_{rad} \cdot \frac{180°}{\pi} $$
$$ \alpha = 1.107 \ rad \cdot \frac{180°}{\pi} = 63.4264° $$
Therefore, the line forms an angle of 63.4264° with the x-axis.
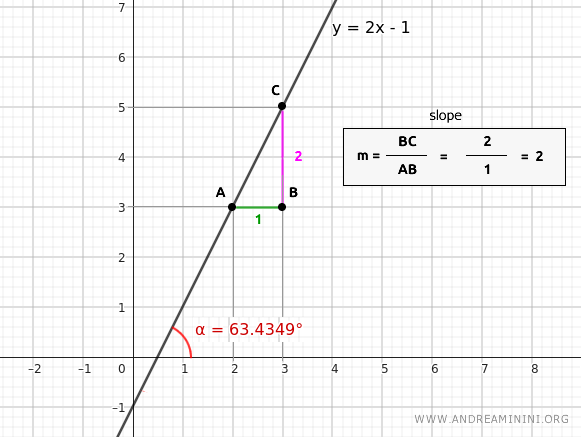
Thus, we have determined the angle α of the line starting from the slope.
And so on.
