Perpendicular Line Theorem for a Point on a Line
Through any point P in a plane, there is exactly one perpendicular line to a given line "r".
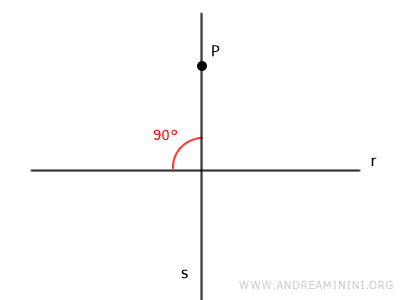
In practice, if we consider any point P in the plane and a line r that does not necessarily pass through point P, there is exactly one line s perpendicular to r that passes through point P.
The point where the perpendicular line intersects line r is called the foot of the perpendicular.
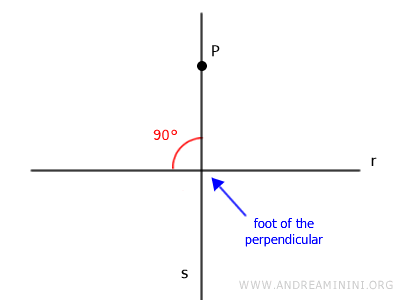
This theorem is also known as the theorem of the existence and uniqueness of the perpendicular from a point to a line.
Proof
Let $ P $ be a point located outside the line $ r $, and let $ s \perp r $ be the perpendicular to $ r $ passing through $ P $.
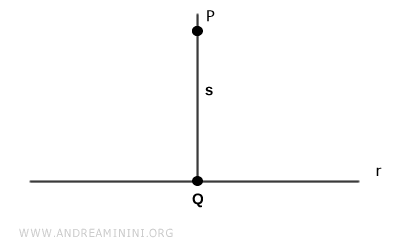
Denote by $ Q $ the foot of the perpendicular from $ P $ to $ r $.
Choose two distinct points $ A $ and $ B $ on line $ r $ such that both are equidistant from $ Q $.

Draw the segments $ AP $ and $ BP $.
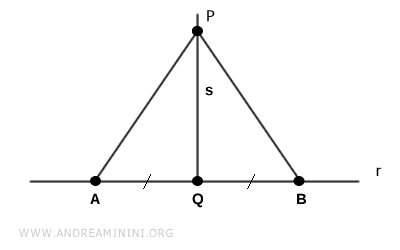
By construction, segment $ PQ $ bisects angle $ A \hat P B $, and since $ PQ $ lies on $ s $, the bisector of the angle is also perpendicular to $ r $.
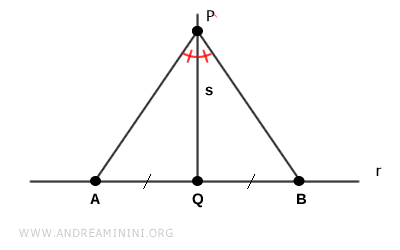
Because the bisector of an angle is unique, it follows that the perpendicular $ s $ from point $ P $ to line $ r $ is also unique.
An Alternative Proof
The proof is divided into two parts.
We need to distinguish between the situation where point P lies on line "r" and when it does not.
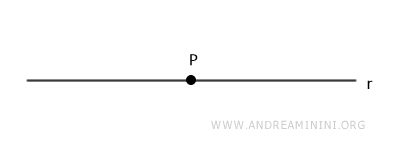
A] Point P lies on the line (P ∈ r)
Consider a line r in the plane and any point P on line r.
Using a compass centered at point P, draw two points A and B on the line with any opening.
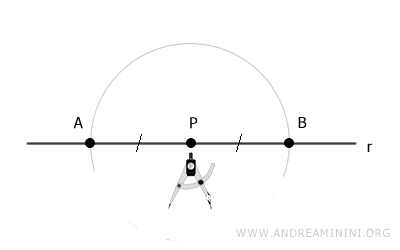
Points A and B are equidistant from point P, so segments AP and BP are congruent, meaning they have the same length.
$$ AP \cong BP $$
Therefore, point P is the midpoint of segment AB.
Next, center the compass at A and draw an arc with radius AB.
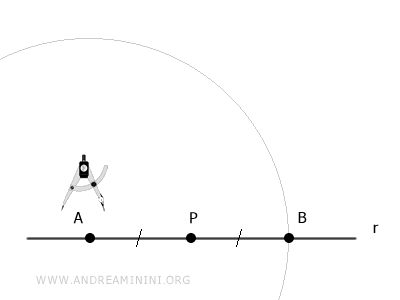
Center the compass at B and draw a second arc with the same radius.
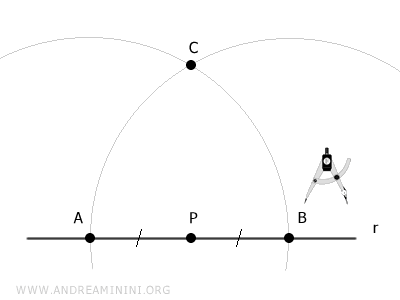
The intersection point of the two arcs is point C.
Note: You can use a radius different from AB as long as it is greater than AP to ensure the two arcs intersect.
There is exactly one line passing through two distinct points in the plane.
Therefore, there is exactly one line s passing through points P and C.
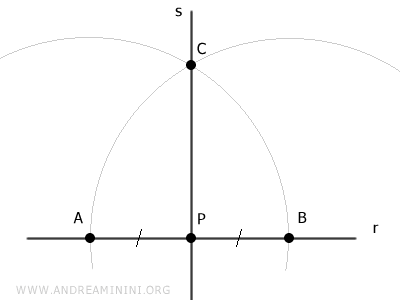
Line s is perpendicular to line r because if we consider triangle ABC, it is an isosceles triangle as sides AC and BC are congruent by construction (AC≅BC).
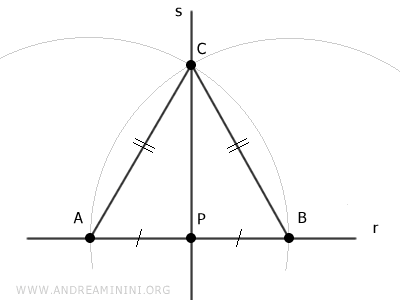
Segment CP is the median of the triangle because it connects vertex C with the midpoint P of the opposite side AB.
Knowing that in an isosceles triangle the median coincides with the altitude, we deduce that segment CP forms a right angle with base AB.
Therefore, line s containing segment CP is perpendicular to line r.
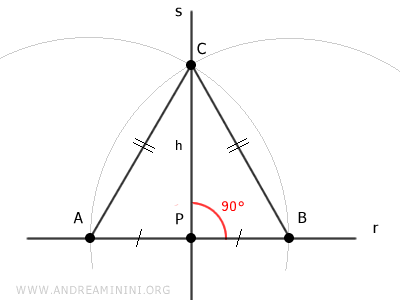
This demonstrates the existence and uniqueness of the perpendicular line.
Note: The uniqueness is demonstrated by the fact that there is only one line passing through two distinct points C and P. Additionally, triangle ABC is isosceles, and in isosceles triangles, the median CP also coincides with the angle bisector at vertex C. Knowing that an angle has only one bisector further proves the uniqueness of line s.
B] Point P does not lie on the line (P ∉ r)
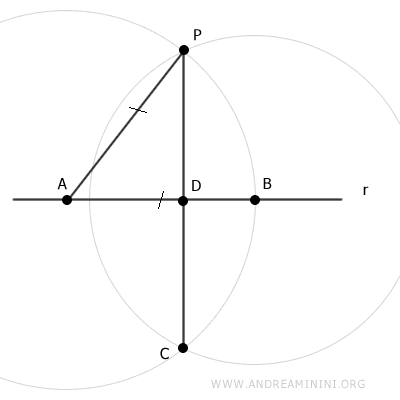
Consider a line r and a point P in the plane that does not lie on the line.
Choose any point A on line r and draw segment AP.
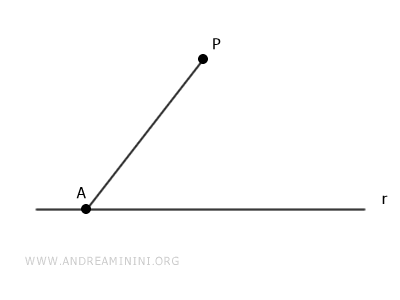
Center the compass at point A and draw an arc with radius AP.
The intersection of the arc with line r is point B.
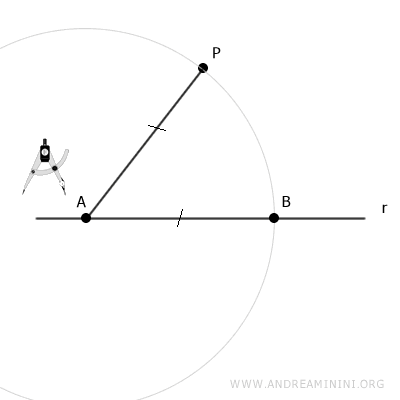
By construction, segments AP and AB are congruent.
$$ \overline{AP} \cong \overline{AB} $$
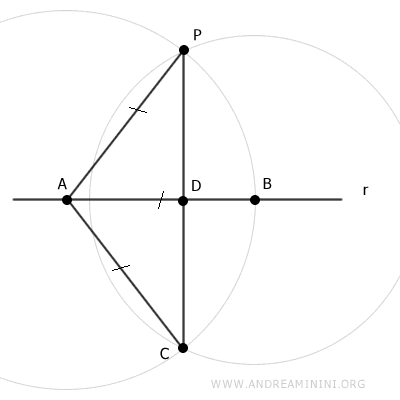
Center the compass at point B and draw a second arc with radius BP.
The two arcs intersect at points P and C.
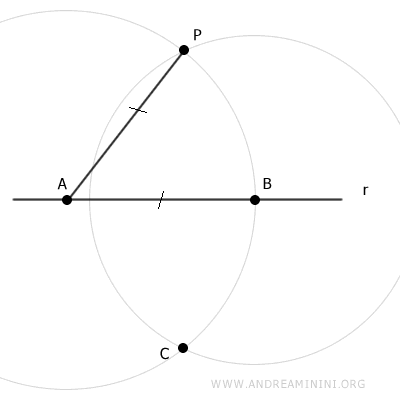
Draw segment CP between points P and C.
Segment CP intersects line r at point D.
Draw segment AC, which by construction is congruent to segment AP (AC≅AP).
Draw segments BP and BC, which are congruent by construction (BP≅BC).
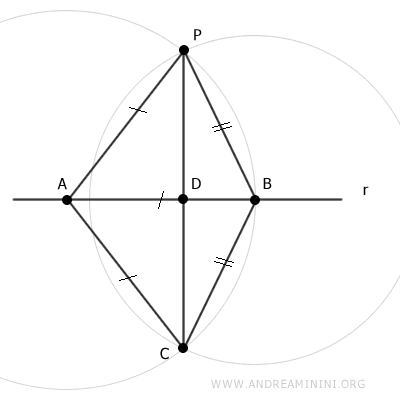
According to the third triangle congruence criterion (SSS), triangles APB and ACB are congruent because they share side AB and have two congruent sides AP≅AC and BP≅BC.
$$ APB \cong ACB $$
Thus, triangles APB and ACB have congruent angles in the same order.
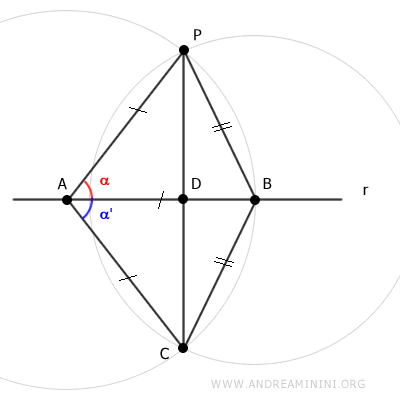
We are particularly interested in the congruence of angles α≅α'.
This allows us to assert that triangles APD and ACD are congruent because they have a congruent angle (α≅α'), a congruent side (AP≅AC), and a common side (AD).
$$ APD \cong ACD $$
Consequently, sides PD and CD are congruent (PD≅CD).
Therefore, point D is the midpoint of segment PC.
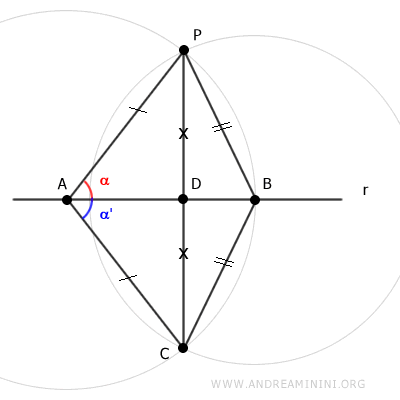
Now consider triangle APC, which is an isosceles triangle because it has two congruent sides AP and AC.
Segment AD is the median of triangle APC because it connects vertex A with the midpoint D of the opposite side PC.
In isosceles triangles, the median coincides with the height and the angle bisector.
Note: By definition, the height of a triangle is a segment that connects a vertex with a point on the opposite side (or its extension) forming a right angle.
Therefore, segment AD is perpendicular to segment PC.
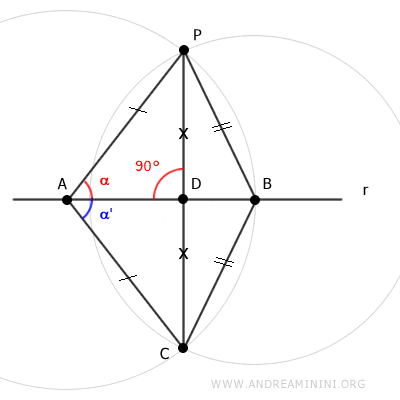
Therefore, knowing that there is only one line passing through two distinct points, line s passing through points P and C is perpendicular to line r passing through points A and B.
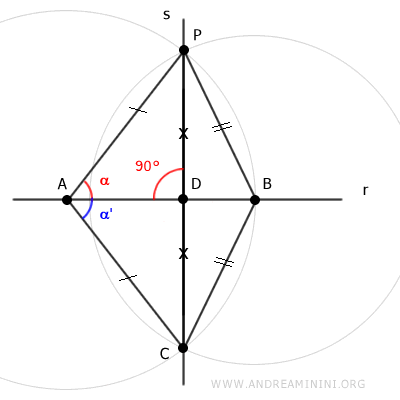
Note: Besides the fact that there is only one line passing through two distinct points, the uniqueness is also demonstrated by the fact that triangle APC is isosceles, and in isosceles triangles, the median AD coincides with the angle bisector at vertex A. Therefore, line r is perpendicular to line s and vice versa.
Thus, we have proven that there is exactly one line s perpendicular to line r passing through point C.
$$ r \perp s $$
Verification: If we take any other point E on line r different from point D, knowing that segment PD is perpendicular to line r, the points PDE form a right triangle.
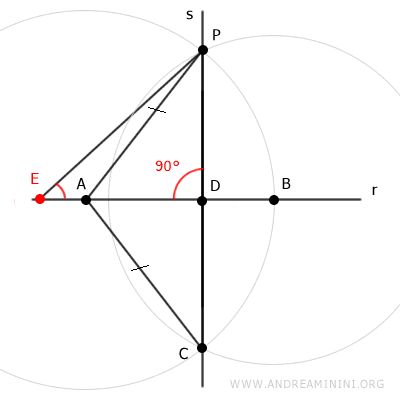
In a right triangle, only one angle can be a right angle (90°). In this case, it is the right angle (90°) at vertex D. Therefore, the other two angles of triangle PDE must be acute (<90°). This implies that segment PE cannot be perpendicular to line r. The same reasoning applies to any point E on line r different from point D.
And so forth.
