Third Criterion for Triangle Congruence

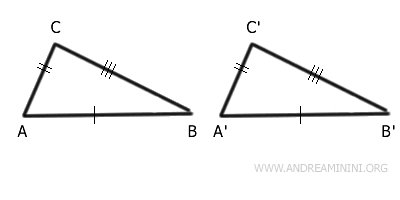
Two triangles are congruent if all their sides are congruent in the same order.

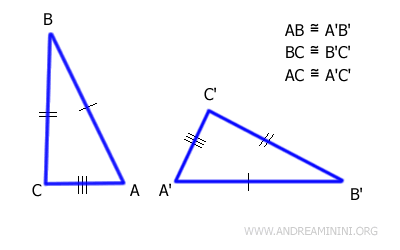
In other words, two triangles are considered congruent when all their corresponding sides are equal in length and match up in the same sequence.

This criterion is also known as SSS (Side-Side-Side)

For example, consider two triangles ABC and A'B'C'.

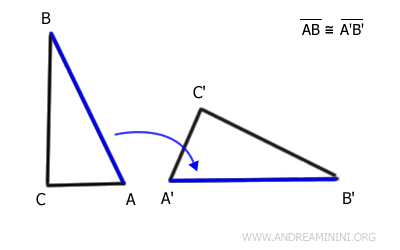
After a rigid transformation (translation + rotation), side AB of the first triangle overlaps perfectly with side A'B' of the second triangle.

Thus, sides AB and A'B' are equal in length, meaning they are congruent.

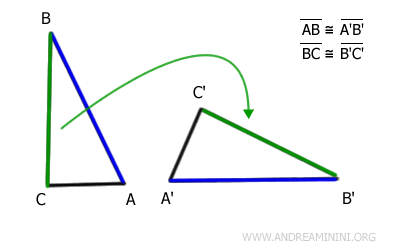
Next, let’s look at the segments following AB and A'B', which are BC and B'C'.

After another rigid transformation, involving translation and rotation, segment BC of the first triangle aligns perfectly with segment B'C' of the second triangle.

Therefore, segments BC and B'C' are equal in length and are congruent.

Finally, let’s consider the segments following BC and B'C', which are AC and A'C'.

After one more rigid transformation, combining translation and rotation, segment AC of the first triangle exactly overlaps segment A'C' of the second triangle.

As a result, segments AC and A'C' are equal in length and are congruent.

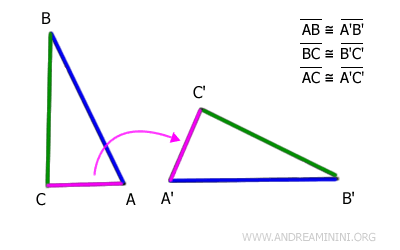
All the segments of the two triangles are congruent in the same order.

Therefore, the two triangles are congruent.

The Proof

This is a theorem because it can be proven.

Consider the two triangles ABC and A'B'C' from the previous example.

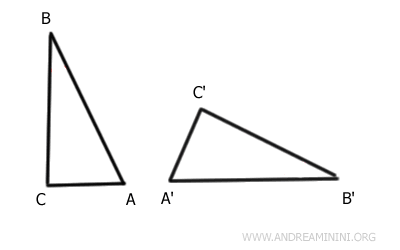
The two triangles have all their sides congruent in the same order.

$$ \overline{AB} \cong \overline{A'B'} $$

$$ \overline{BC} \cong \overline{B'C'} $$

$$ \overline{AC} \cong \overline{A'C'} $$

We need to prove that the two triangles ABC and A'B'C' are indeed congruent.

Using a rigid transformation (translation + rotation + reflection), I align sides AB and A'B' of the two triangles.

 

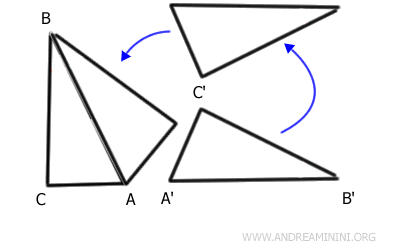
I label the new vertex C''

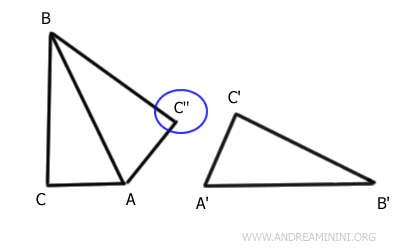
Therefore, triangles AC''B and A'B'C' are congruent.

$$ AC''B \cong A'B'C' $$

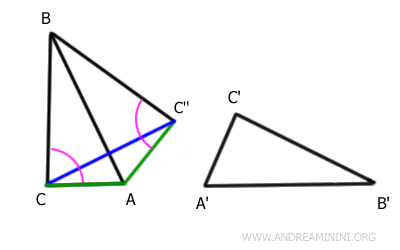
I draw a segment connecting points C and C''.

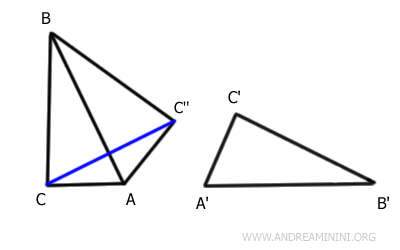
Triangle AC''C is an isosceles triangle with base CC'' because AC ≅ A'C' ≅ AC''

Knowing that the base angles of an isosceles triangle are congruent, I deduce that the angles at vertices C and C'' are congruent.

$$ A \hat{C} C \text{''} \cong A \hat{C} \text{''} C $$

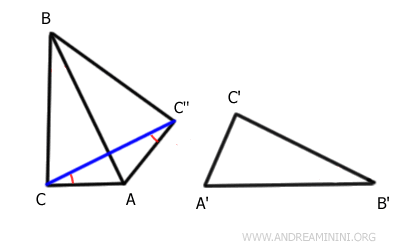
Similarly, triangle CBC'' is an isosceles triangle with base CC'' because BC ≅ B'C' ≅ BC''

Considering that in an isosceles triangle the base angles are congruent, I can affirm that the angles at vertices C and C'' are indeed congruent.

$$ B \hat{C} C \text{''} \cong B \hat{C} \text{''} C $$

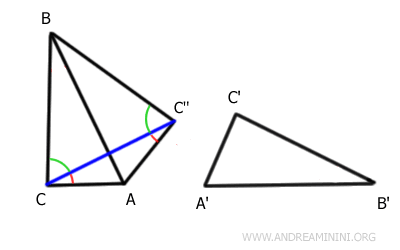
The sums of two pairs of congruent angles are also congruent.

$$ A \hat{C} C \text{''} + B \hat{C} C \text{''} \cong B \hat{C} \text{''} C + A \hat{C} \text{''} C $$

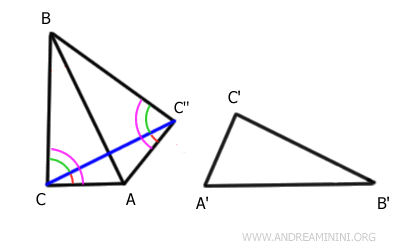
Therefore, the angles (in purple) at vertices C and C'' are congruent.

$$ A \hat{C} B \cong A \hat{C} \text{''} B $$

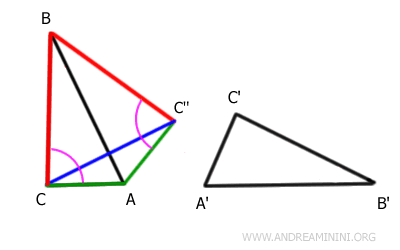
Knowing that triangle ACC'' is isosceles with base CC'', I deduce that sides AC and AC'' are congruent.

$$ \overline{AC} \cong \overline{AC} \text{''} $$

Similarly, knowing that triangle BCC'' is isosceles with base CC'', I deduce that sides BC and BC'' are congruent.

$$ \overline{BC} \cong \overline{BC} \text{''} $$

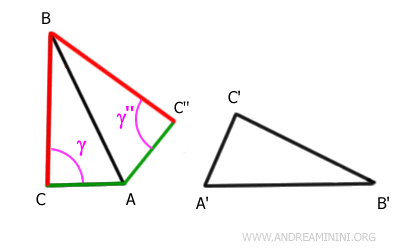
According to the first criterion of congruence, triangles ABC and ABC'' are congruent because they have two congruent sides, BC ≅ BC'' and AC ≅ AC'', and the included angle γ = γ'' is congruent.

$$ ABC \cong ABC'' $$

Since triangle ABC'' is congruent to triangle A'B'C' by the initial construction:

$$ ABC'' \cong A'B'C' $$

By the transitive property, triangle ABC is congruent to triangle A'B'C'

$$ ABC \cong ABC'' \cong A'B'C' $$

Therefore:

$$ ABC \cong A'B'C' $$

This is what we wanted to prove.

Alternative Proof

Let's consider two triangles, ABC and A'B'C', where the corresponding sides are congruent in the same order.

$$ \overline{AB} \cong \overline{A'B'} $$

$$ \overline{BC} \cong \overline{B'C'} $$

$$ \overline{AC} \cong \overline{A'C'} $$

We want to prove that, given these conditions, triangles ABC and A'B'C' are congruent.

We draw a ray A''B that forms the same angle $ \beta' $ at vertex B and has the same length as segment A'B'.

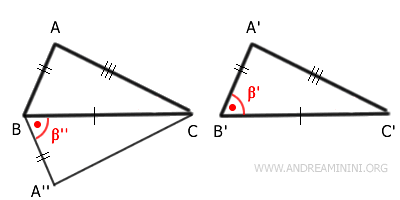
By construction, the segments $ \overline{A'B'} \cong \overline{A''B} $ and the angles $ \beta' \cong \beta'' $ are congruent.

Now, triangles A''BC and A'B'C' share a congruent side by hypothesis, $ \overline{BC} \cong \overline{B'C'} $, a second congruent side by construction, $ \overline{A'B'} \cong \overline{A''B} $, and the included angle is also congruent, $ \beta' \cong \beta'' $.

By the first triangle congruence theorem, it follows that $ A''BC \cong A'B'C' $.

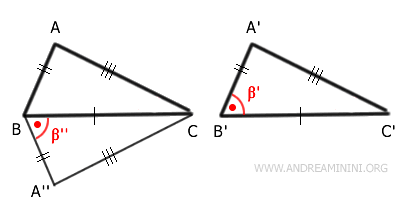
Next, we connect points A and A'' with the segment $ \overline{AA''} $.

Triangle ABA'' is isosceles since its two oblique sides are congruent: $ \overline{AB} \cong \overline{A''B} $. As a result, the angles $ B\hat{A}A'' \cong B''A $ are also congruent.

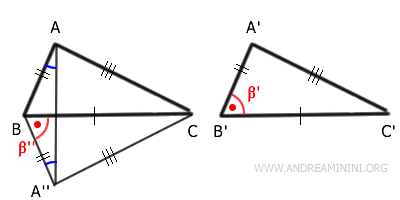
Similarly, triangle $ ACA'' $ is also isosceles since its oblique sides $ \overline{AC} \cong \overline{A''C} $ are congruent.

It follows that the base angles of the isosceles triangle are also congruent: $ C \hat{A}A'' \cong C \hat{A''}A $.

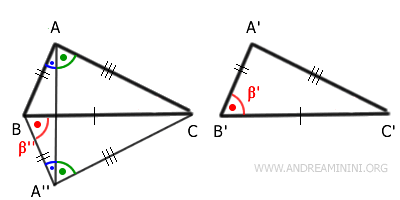
Furthermore, the angles $ B \hat{A} C \cong B \hat{A''} C $ (i.e., $ \alpha \cong \alpha'' $) are also congruent, as they are sums of congruent angles.

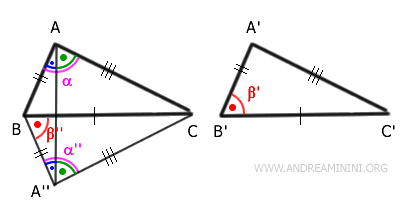
Applying the first congruence theorem once again, we conclude that triangles $ ABC \cong A''BC $ as they have two congruent sides, $ AB \cong A''B $ and $ AC \cong A''C $, with a congruent included angle, $ \alpha \cong \alpha'' $.

$$ ABC \cong A''BC $$

Since we have already established that $ A''BC \cong A'B'C' $, the transitive property tells us that $ ABC \cong A'B'C' $ as well.

$$ ABC \cong A''BC \cong A'B'C' $$

Thus, the proof is complete.

And so on.