Circumcenter

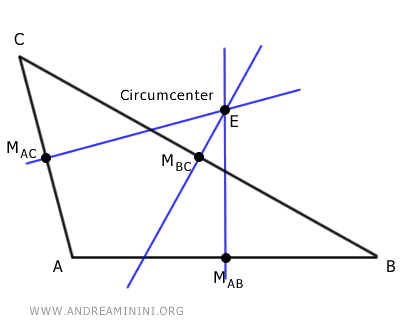
The circumcenter of a triangle is the point where the perpendicular bisectors of the triangle intersect. These are the lines that are perpendicular to the sides of the triangle and pass through their midpoints.

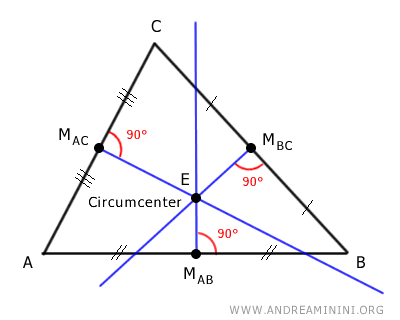
The lines perpendicular to the midpoints of each side of the triangle are also known as perpendicular bisectors.

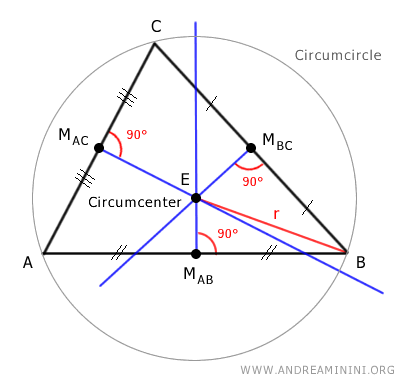
The circumcenter is also the center of the circumscribed circle, called the circumcircle, which passes through all three vertices of the triangle.

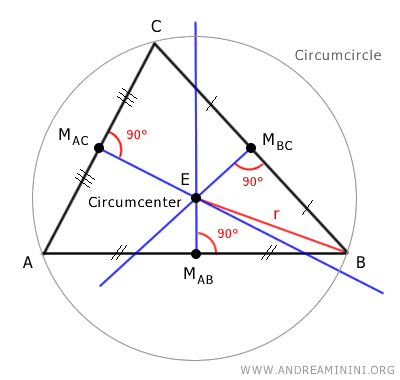
Center of the Circumcircle. The circumcenter is the center of the circle that passes through the vertices of the triangle. Therefore, the circumcenter is equidistant from the three vertices of the triangle. This distance is called the radius of the circumcircle (r).

How to Find the Circumcenter

Let's consider a triangle ABC.

The triangle has three vertices: A, B, and C, and three sides: AB, BC, and AC.

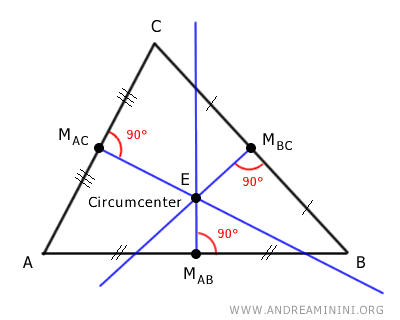
Identify the midpoint of each side of the triangle: M_AB, M_BC, and M_AC.

What is the midpoint? The midpoint of a segment is the point that divides the segment into two equal parts.

For each side of the triangle, draw the perpendicular bisector passing through the midpoint.

Each perpendicular bisector forms a right angle (90°) with the side of the triangle.

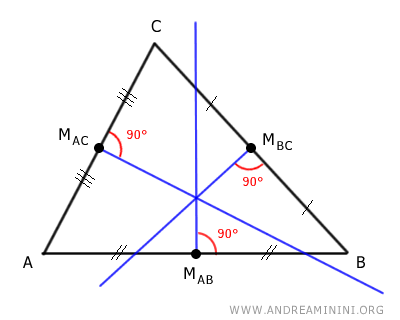
The intersection point of the three perpendicular bisectors is the circumcenter.

Now, draw a segment r from the circumcenter to one of the vertices of the triangle, for example, vertex B.

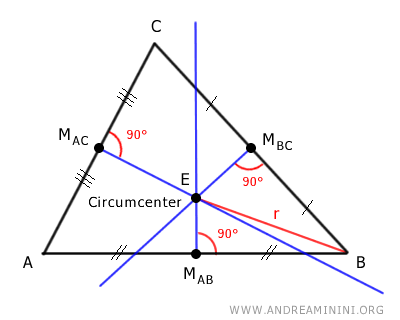
This segment r is the radius of the circumcircle, which passes through all the vertices of the triangle.

The Proof

The proof of the circumcenter's existence is quite straightforward.

Consider any triangle ABC.

Through any three distinct, non-collinear points, there can be exactly one circle.

Therefore, a triangle can always be circumscribed by a circle because there is exactly one circle that passes through the three vertices of a triangle, with its center at the circumcenter (O).

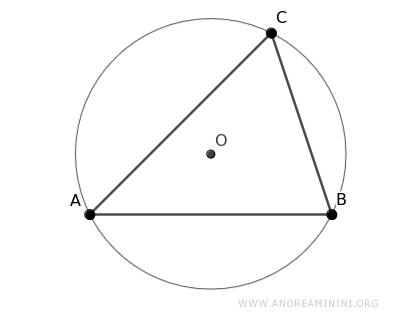
By construction, the side AB of the triangle is a chord of the circle.

Knowing that the perpendicular bisector of a chord always passes through the center of the circle, we deduce that the perpendicular bisector of segment AB passes through the center of the circle O (the circumcenter).

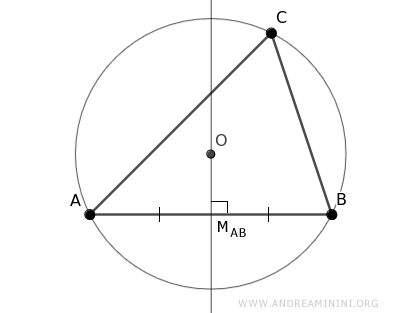
The same logic applies to the other sides BC and AC because they are also chords of the circle.

Draw the perpendicular bisectors from the midpoints of these sides (segment bisectors) and they also pass through the circumcenter O.

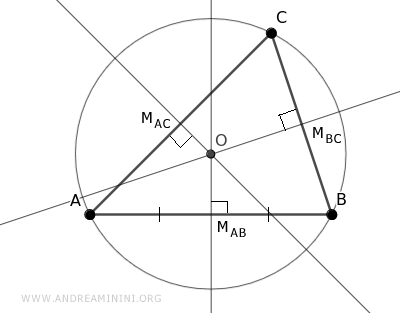
This demonstrates that the intersection point of the triangle's bisectors is the center of the circle that circumscribes the triangle.

 

Observations

Some observations and characteristics of the circumcenter:

• The position of the circumcenter depends on the type of triangle
  • In an acute triangle, the circumcenter is inside the triangle.
    
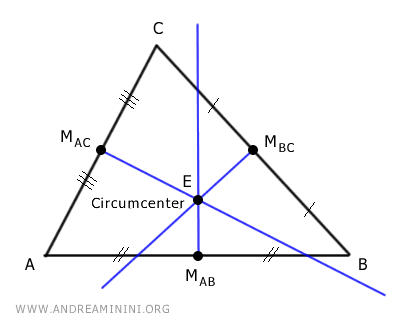
  • In an obtuse triangle, the circumcenter is outside the triangle.
    
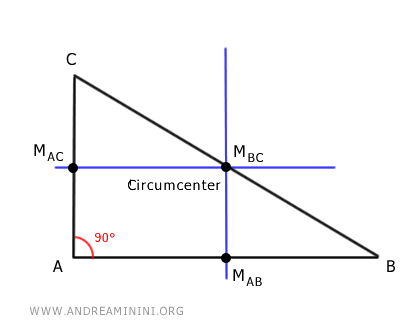
  • In a right triangle, the circumcenter is on the hypotenuse. In the case of a right triangle, the circumcenter coincides with the midpoint of the hypotenuse (M_BC).
    
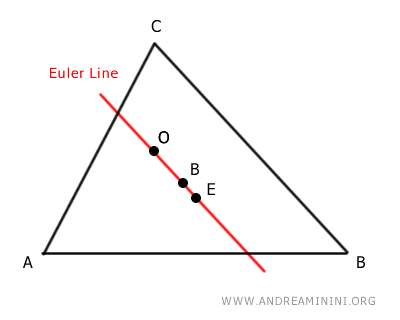
• The circumcenter always lies on the Euler line
  The Euler line is the line passing through the centroid (B), the circumcenter (E), and the orthocenter (O) of a triangle.
  

And so on.