Centroid of a Triangle

The centroid of a triangle is the internal point where its medians intersect.

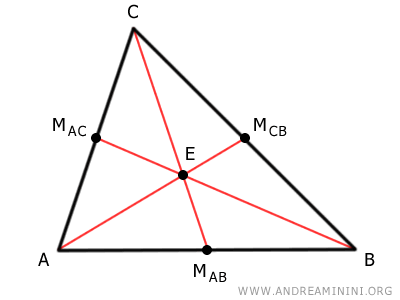
A median of a triangle is a segment that connects a vertex to the midpoint of the opposite side.

Every triangle has three vertices (A, B, C) and three sides (AB, CB, AC), so it has three medians.

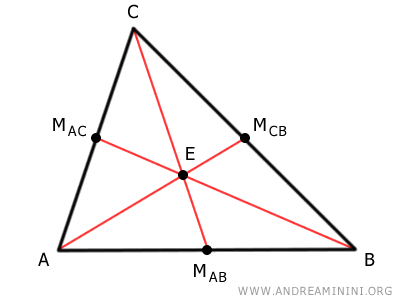
The three medians AM_CB, BM_AC, and CM_AB meet at an internal point (E) of the triangle called the centroid.

What is it used for? The centroid is also the triangle's balance point and represents a point of equilibrium. The term "centroid" comes from the Greek word "barys," meaning "heavy," and "center." For example, if you were to place the triangle on a small support precisely at its centroid, it would remain perfectly balanced. Generally, the centroid is very useful for studying the balance of forces on a shape or object.

How to Find the Centroid

Consider any triangle ABC.

First, identify the midpoints of each side of the triangle.

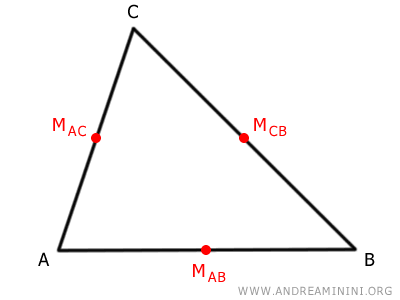
What is a midpoint? The midpoint of a segment is the point that divides it into two equal parts, meaning it is equidistant from both ends of the segment.

Draw the three medians of the triangle, connecting each vertex with the midpoint of the opposite side.

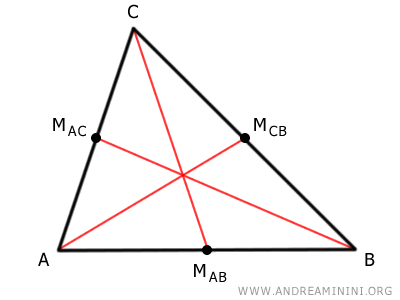
The intersection point of the medians (E) is the centroid of the triangle.

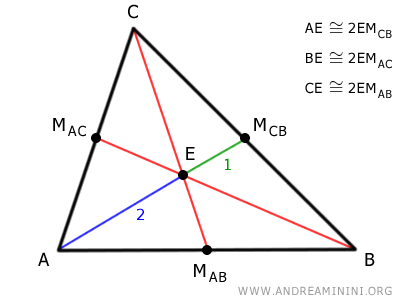
The Centroid Divides the Median in a 2:1 Ratio

The segment from the vertex to the centroid is twice as long as the segment from the centroid to the midpoint of the opposite side.

Thus, the centroid is located at 2/3 of the length of the median from the vertex.

Proof

Consider a triangle ABC.

Identify the midpoints M and N of two sides of the triangle and draw the corresponding medians.

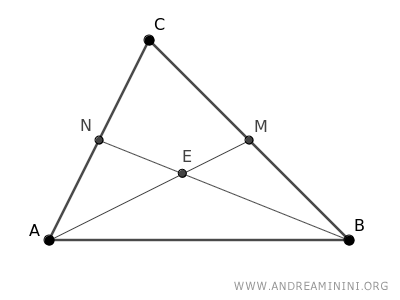
The two medians meet at point E.

Identify the midpoints of the segments AE and BE.

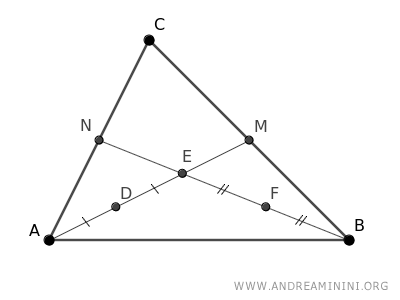
Being midpoints, the segments AD≅ED and BF≅EF are equal.

$$ \overline{AD} \cong \overline{ED} $$

$$ \overline{BF} \cong \overline{EF} $$

Draw the segment between the midpoints M and N.

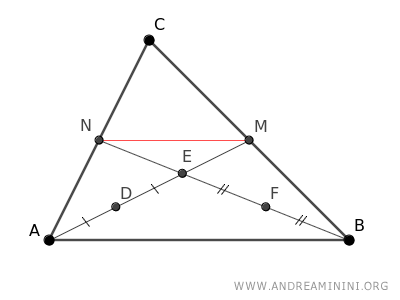
According to the midline theorem, the segment MN connecting two midpoints of the sides of triangle ABC is parallel to the third side AB and half its length.

$$ \overline{MN} \parallel \overline{AB} $$

$$ \overline{MN} \cong \frac{1}{2} \cdot \overline{AB} $$

Draw the segment DF between the two midpoints of triangle ABE.

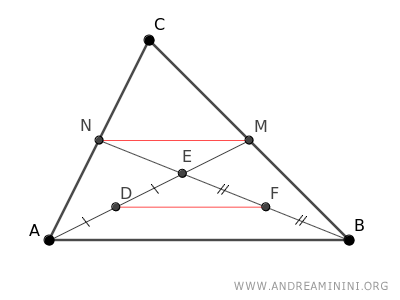
Again, according to the midline theorem, the segment DF connecting two midpoints of the sides of triangle ABE is parallel to the third side AB and half its length.

$$ \overline{DF} \parallel \overline{AB} $$

$$ \overline{DF} \cong \frac{1}{2} \cdot \overline{AB} $$

Therefore, the segments DF and MN are congruent and parallel to AB.

$$ \overline{DF} \cong \overline{MN} \cong \frac{1}{2} \cdot \overline{AB} $$

The quadrilateral DFMN is a parallelogram because it has parallel opposite sides DF||MN and equal sides DF≅MN.

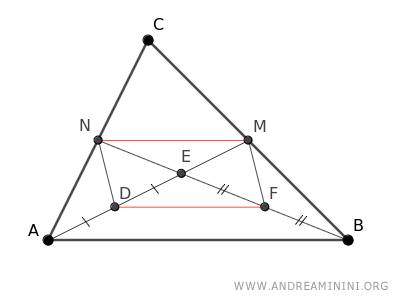
Knowing that the diagonals of a parallelogram intersect at their midpoints, I deduce that the segments EN≅EF and ED≅EM are equal.

$$ \overline{EN} \cong \overline{EF} $$

$$ \overline{ED} \cong \overline{EM} $$

Since ED≅AD and EF≅BF, by transitive property EN≅EF≅BF and EM≅ED≅AD

Graphically,

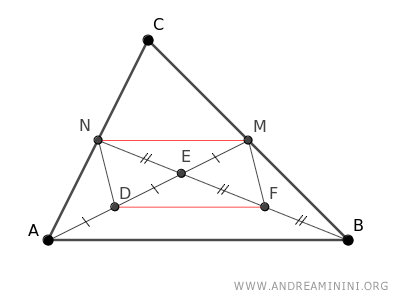
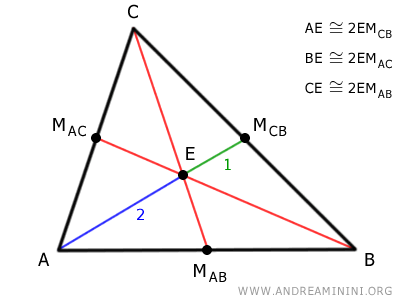
This means that segment AE is twice the length of segment EM.

$$ \overline{AE} = 2 \overline{EF} $$

Similarly, segment BE is twice the length of segment EN.

$$ \overline{BE} = 2 \overline{EN} $$

This proves that the centroid divides the median into two segments in a 2:1 ratio

This reasoning can be repeated for each median of the triangle.

The Centroid in Analytical Geometry

To find the coordinates of the centroid \(G(x, y)\) of a triangle with vertices \(A(x_1, y_1)\), \(B(x_2, y_2)\), and \(C(x_3, y_3)\) in a Cartesian coordinate system, use the following formulas: $$ x = \frac{x_1 + x_2 + x_3}{3} $$ $$ y = \frac{y_1 + y_2 + y_3}{3} $$

These formulas are obtained by taking the arithmetic mean of the \(x\ ) and \(y\) coordinates of the three vertices of the triangle.

The centroid is thus located exactly at the "center" of the triangle in terms of the average coordinates of its vertices.

Example

Consider this triangle ABC

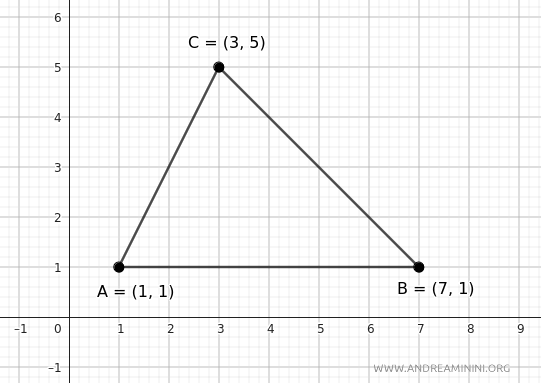
The vertices of the triangle are at the Cartesian coordinates A(1,1), B(7,1), and C(3,5).

$$ A(x_1, y_1)= (1,1) $$

$$ B(x_2, y_2)= (7,1) $$

$$ C(x_3, y_3)= (3,5) $$

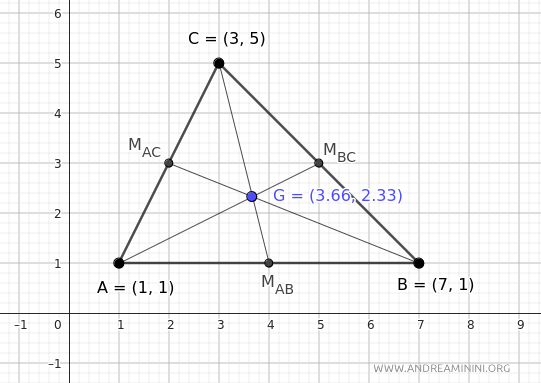
To find the coordinates of the centroid G(x,y) of the triangle, apply the previous formulas:

$$ \begin{cases} x = \frac{x_1 + x_2 + x_3}{3} \\ \\ y = \frac{y_1 + y_2 + y_3}{3} \end{cases} $$

Substitute the coordinates of vertex A (x₁=1, y₁=1), vertex B (x₂=7, y₂=1), and vertex C (x₃=3, y₃=5).

$$ \begin{cases} x = \frac{1 + 7 + 3}{3} \\ \\ y = \frac{1 + 1 + 5}{3} \end{cases} $$

$$ \begin{cases} x = \frac{11}{3} \\ \\ y = \frac{7}{3} \end{cases} $$

$$ \begin{cases} x = 3.66 \\ \\ y = 2.33 \end{cases} $$

Therefore, the centroid G of the triangle is at the coordinates (x, y) = (3.66, 2.33).

Proof

To prove the analytical formulas, consider a triangle ABC.

The centroid G of the triangle is at the intersection of the medians.

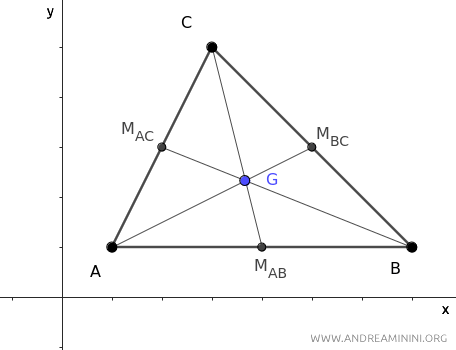
Each median is the segment that connects a vertex of the triangle to the midpoint M of the opposite side.

The centroid divides each median into two parts, with the part containing the vertex being twice the length of the other.

For example, if we consider the median AM_BC, the segment AG is twice the length of segment GM_BC.

$$ \overline{AG} = 2 \cdot \overline{GM}_{BC} $$

Now project points A, G, and M_BC of median AM_BC onto the x-axis.

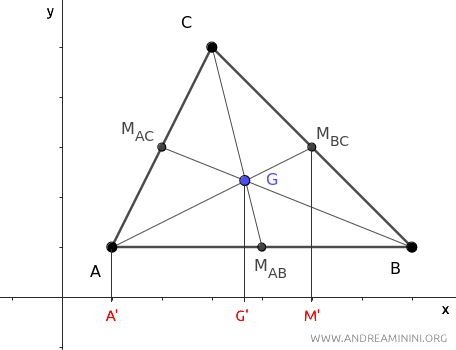
The line A'M' is the projection of the median AM_BC onto the x-axis of the Cartesian plane.

The projections of the points onto the x-axis form a set of parallel lines that intersect the two transversal segments AM_BC and A'M'.

According to Thales' theorem, when a set of parallel lines intersects two transversal segments, the corresponding segments on the transversals are directly proportional.

Thus, if segment AG is twice the length of GM_BC, then the projected segment A'G' is also twice the length of G'M'.

$$ \overline{A'G'} = 2 \cdot \overline{G'M'} $$

Next, measure the lengths of the projected segments on the x-axis.

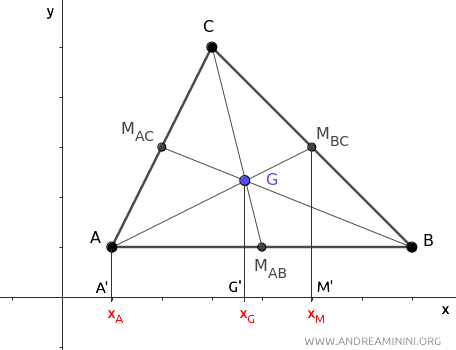
Segment A'G' measures x_G-x_A, while segment G'M' measures x_M-x_G.

Substitute these measurements into the previous equation:

$$ \overline{A'G'} = 2 \cdot \overline{G'M'} $$

$$ x_G - x_A = 2 \cdot ( x_M - x_G ) $$

$$ x_G - x_A = 2 x_M - 2x_G $$

$$ x_G + 2x_G = 2 x_M + x_A $$

$$ 3x_G = 2 x_M + x_A $$

$$ x_G = \frac{ 2 x_M + x_A }{3} $$

Knowing that the point x_M is the projection of the midpoint M_BC onto the x-axis, i.e., $ x_M = \frac{x_B+x_C}{2} $.

$$ x_G = \frac{ 2 \cdot \frac{x_B+x_C}{2} + x_A }{3} $$

$$ x_G = \frac{ x_A + x_B + x_C }{3} $$

This proves the formula for the x-coordinate of the centroid on the Cartesian plane.

To prove the y-coordinate, follow a similar procedure.

This time, project points A, G, and M_BC of median AM_BC onto the y-axis.

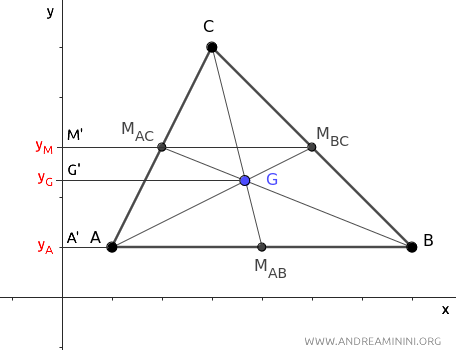
According to Thales' theorem, if segment AG is twice the length of GM_BC, then the projected segment A'G' on the y-axis is also twice the length of G'M'.

$$ \overline{A'G'} = 2 \cdot \overline{G'M'} $$

Segment A'G' on the y-axis measures y_G-y_A, while segment G'M' measures y_M-y_G.

$$ y_G - y_A = 2 \cdot ( y_M - y_G ) $$

$$ y_G - y_A = 2 y_M - 2 y_G $$

$$ y_G + 2 y_G = y_A + 2 y_M $$

$$ 3y_G = y_A + 2 y_M $$

$$ y_G = \frac{ y_A + 2 y_M }{3} $$

Knowing that the point y_M is the projection of the midpoint M_BC onto the y-axis, i.e., $ y_M = \frac{y_B+y_C}{2} $.

$$ y_G = \frac{ y_A + 2 \cdot \frac{y_B+y_C}{2} }{3} $$

$$ y_G = \frac{ y_A + y_B + y_C }{3} $$

This proves the formula for the y-coordinate of the centroid of the triangle on the Cartesian plane.

Observations

Some observations and properties of the centroid:

• The centroid is always an internal point of the triangle.
• There is only one point of intersection of the medians of a triangle
  By definition, the centroid is the point where the medians intersect. Additionally, it is proven that the centroid divides each median in a 2:1 ratio. Knowing that in any segment, there is one and only one point that can divide it in a 2:1 ratio, once it is known that point E on median AM_CB divides it in a 2:1 ratio, the same point E must divide the other medians of the triangle in the same ratio. There cannot be any other points. In conclusion, there is only one point where the medians can be divided in a 2:1 ratio, and that is the point of intersection of the medians.
  
• The centroid is the center of gravity of the triangle
  In other words, it is a balance point. For example, if you place the triangle on a nail exactly at its centroid, the triangle will remain in balance.

  Note. Knowing the centroid allows me to determine the center of gravity of a shape and helps me understand the distribution of forces.

• Any rigid motion (e.g., rotation, translation) does not change the internal position of the centroid. The centroid moves or rotates with the triangle.
• In the special case of an equilateral triangle, the centroid coincides with the incenter, circumcenter, and orthocenter.
  

And so on.