The Angle Bisector of a Triangle Vertex

In a triangle, the angle bisector of a vertex is a segment that divides an angle into two equal parts. It extends from the vertex of the angle to a point on the opposite side.

Every triangle has three angle bisectors, one for each vertex.

For example, consider triangle ABC.

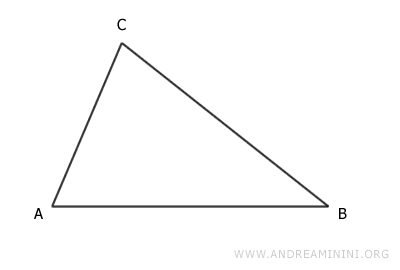
The angle bisector of vertex A is the segment that divides the angle at vertex A into two equal parts.

This segment, AM, connects vertex A to a point M on the opposite side, CB.

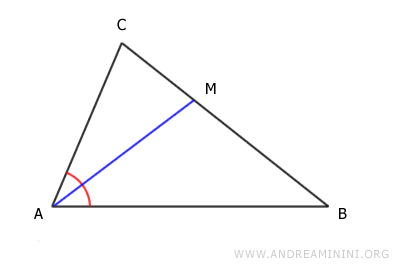
Note: Unlike an angle bisector, which is a ray, the bisector of a vertex is a segment. See the angle bisector for comparison.

The angle bisector of vertex B is a segment BM that divides the angle at vertex B into two equal parts and connects vertex B to a point M on the opposite side, AC.

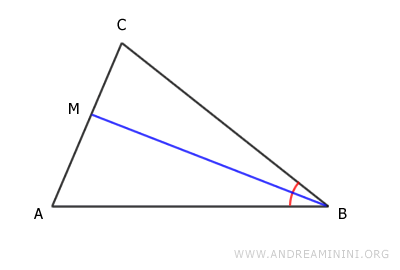
Similarly, the angle bisector of vertex C is a segment CM that divides the angle at vertex C into two equal parts and connects vertex C to a point M on the opposite side, AB.

The three angle bisectors of a triangle intersect at a point called the incenter.

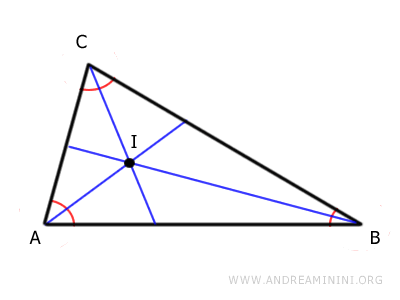
The incenter is the center of a circle, known as the incircle, which is tangent to the sides of the triangle.

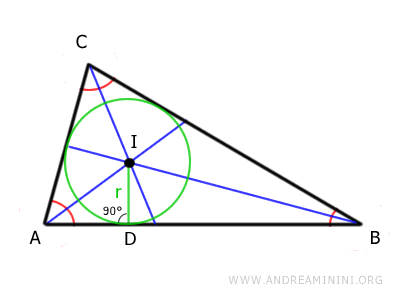
The radius of the incircle is called the inradius.

And so on.