Euclid's First Theorem
In a right triangle, the square constructed on one leg is equal in area to the rectangle formed by projecting that leg onto the hypotenuse, with the height matching the hypotenuse.
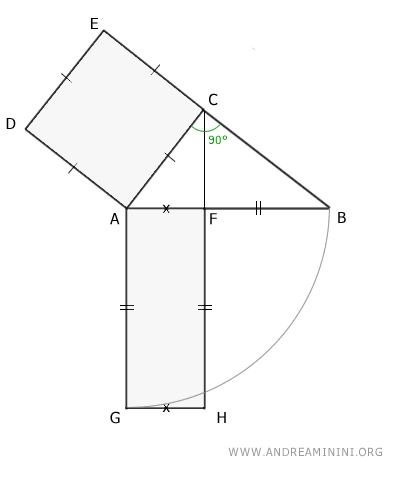
In other words, if we project the legs AC or BC of a right triangle onto the hypotenuse AB, we get two segments, AF and BF, such that:
$$ \overline{AF} + \overline{BF} = \overline{AB} $$
Euclid's theorem states that the area of the square constructed on AC, which is AC2, is equal to the area AB·AF of the rectangle formed by AB and AF.
$$ \overline{AC}^2 = \overline{AB} \cdot \overline{AF} $$
Similarly, the same applies to the other leg.
Note. Euclid's first theorem focuses on the proportional relationships between the sides of the right triangle, the projections of the legs onto the hypotenuse, and the hypotenuse itself. This differs from the Pythagorean theorem, which establishes an equality between the areas: the sum of the areas of the squares built on the legs is equal to the area of the square built on the hypotenuse.
As a corollary, it can also be stated that in a right triangle, each leg is the geometric mean between the hypotenuse and its projection on the hypotenuse.
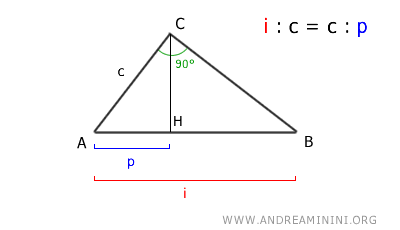
In other words, the hypotenuse (i) is to the leg (c) as the leg (c) is to its projection (p) on the hypotenuse.
Note. The proportion i:c=c:p is entirely equivalent to Euclid's first theorem $$ i : c = c : p \rightarrow c^2 = i \cdot p $$ These are two different ways of expressing the same concept.
A Practical Example
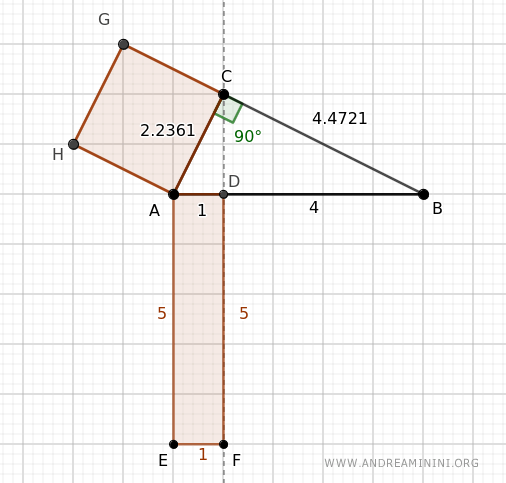
Let's take a right triangle with the following measurements: AB=5, BC=4.4721, and AC=2.2361.
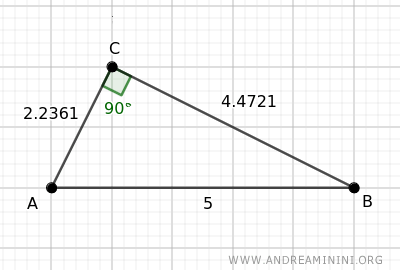
Project the leg AC onto the hypotenuse AB.
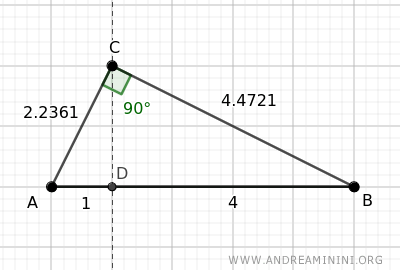
The projection divides the hypotenuse AB=5 into two segments, AD=1 and BD=4.
Now, calculate the area of the square constructed on leg AC:
$$ \overline{AC}^2 = 2.2361^2 = 5 $$
Next, calculate the area of the rectangle formed by the projection of leg AC onto the hypotenuse, which is AD=1, with a length equal to the hypotenuse AB=5.
$$ \overline{AD} \cdot \overline{AB} = 1 \cdot 5 = 5 $$
The areas are the same, as predicted by Euclid's theorem.
Example 2
To complete the example, let's also calculate the square on the other leg BC.
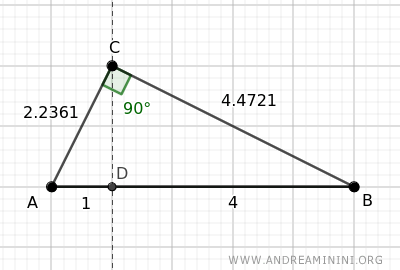
In this case, the square built on the side BC=4.4721
$$ \overline{BC}^2 = 4.4721^2 = 20 $$
Then, calculate the area of the rectangle with the base as the projection of leg BC onto the hypotenuse, which is BD=4, and the length equal to the hypotenuse AB=5.
$$ \overline{BD} \cdot \overline{AB} = 4 \cdot 5 = 20 $$
Again, the result is the same.
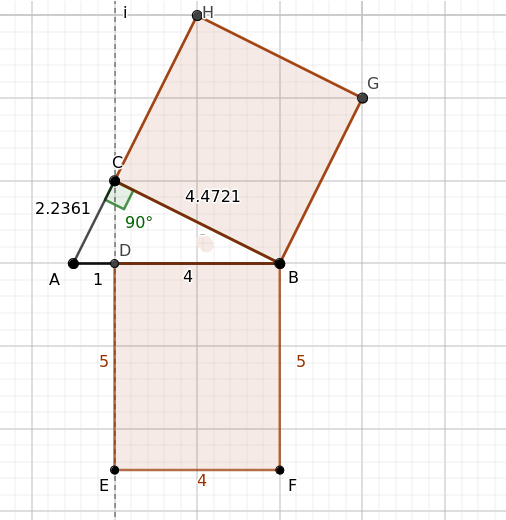
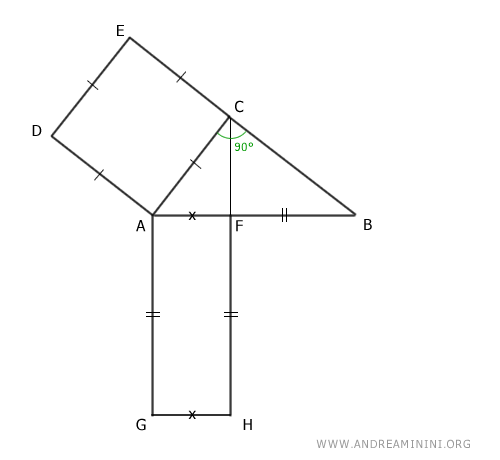
The Proof
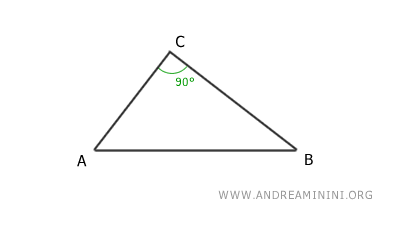
Consider a right triangle ABC.
Construct a square ACED on one leg AC.
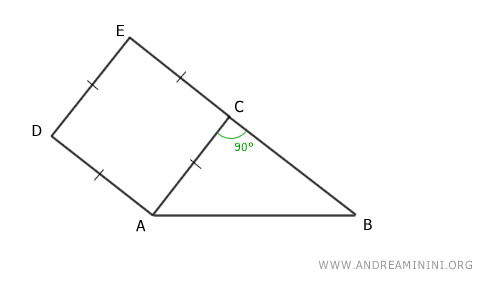
Project the leg AC onto the hypotenuse AB, which is divided into two segments AF and BF.
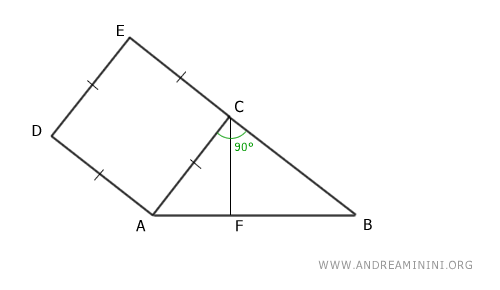
Construct a rectangle on the projection of the leg onto the hypotenuse, with one side equal to the hypotenuse.
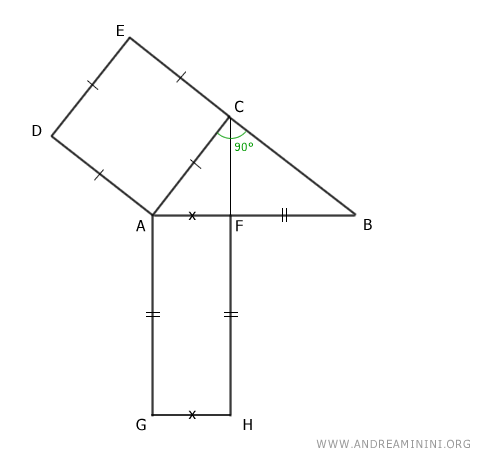
Thus, this rectangle has sides congruent with the hypotenuse.
$$ \overline{AF} \cong \overline{AG} \cong \overline{FH} $$
Draw lines passing through the sides of the rectangle and the line passing through the opposite side of the square to the leg.
Mark the intersection points as K and L.
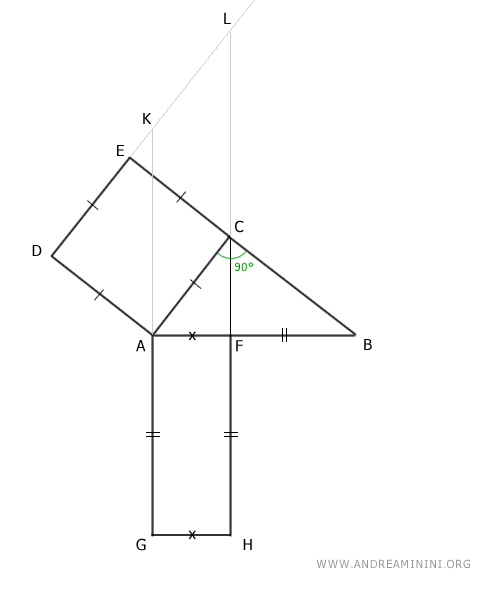
Observe the angles of the square on the leg AC and with respect to the hypotenuse.
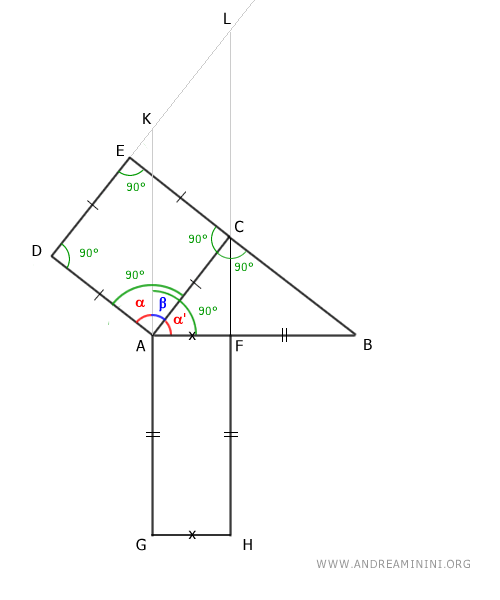
The angles α and α' are congruent α≅α' because they are both complementary to the angle β, as both the square and the rectangle have right angles (90°).
$$ \alpha + \beta = 90° $$
$$ \alpha ' + \beta = 90° $$
Thus, they are congruent:
$$ \alpha + \beta = \alpha ' + \beta $$
$$ \alpha = \alpha ' $$
The triangles AKD and ABC are congruent by the second triangle congruence criterion because they have a congruent side AC≅AD and adjacent angles congruent at 90° and α≅α'.
$$ AKD \cong ABC $$
Being congruent, triangles AKD and ABC have all corresponding sides and angles congruent.
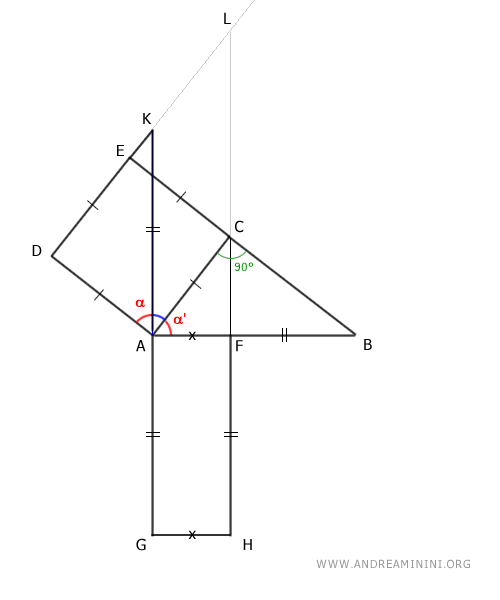
Of particular interest is that sides AK and AB are congruent.
$$ \overline{AK} \cong \overline{AB} $$
By construction, the quadrilateral ACLK is a parallelogram because it has opposite sides parallel.
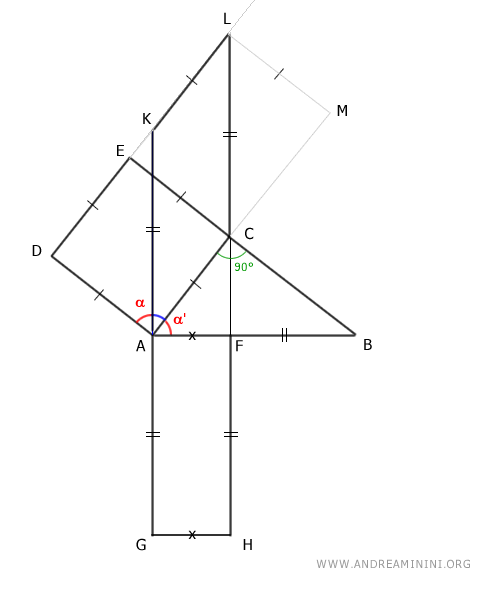
According to the principle of parallelogram equivalence, the square ACED and the parallelogram ACLK are equivalent, having the same base AC and congruent height EA≅LM.
$$ ACED \doteq ACLK $$
For the same reason, the rectangle AFHG and the parallelogram ACLK are also equivalent, having the congruent base AG≅AK and the same height AH.
$$ AFHG \doteq ACLK $$
Therefore, by the transitive property, the square ACED and the rectangle AFHG are equivalent.
$$ ACED \doteq ACLK \doteq AFHG $$
$$ ACED \doteq AFHG $$
Thus, the area of the square constructed on leg AC is equal to the area of the rectangle constructed on the projection of leg AC onto the hypotenuse, with the hypotenuse as one side.
This proves Euclid's theorem for right triangles.
Note. Similarly, the same property can be proven for the other leg BC of the right triangle.
Corollary
In a right triangle, each leg (c) is the geometric mean between the hypotenuse (i) and its projection (p) on the hypotenuse.
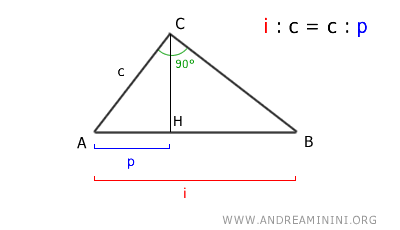
In other words, the hypotenuse is to the leg as the leg is to its projection on the hypotenuse.
$$ i:c = c:p $$
This means that the square of the leg (c) is equal to the product of the hypotenuse (i) and the projection (p) of the leg onto the hypotenuse.
$$ \frac{i}{c} = \frac{c}{p} $$
$$ c^2 = i \cdot p $$
This brings us back to Euclid's first theorem, which states that the area of the square constructed on the leg of the right triangle is equal to the area of the rectangle constructed on the projection of the leg and the hypotenuse.
Example
Let's revisit the previous example of the right triangle ABC, where all measurements are already known.
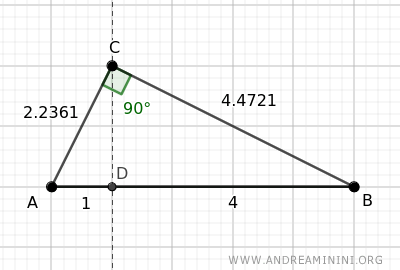
The leg AC measures approximately 2.2361, its projection on the hypotenuse (AD) measures 1, and the hypotenuse AB measures 5.
According to the corollary, the leg AC is the geometric mean between the hypotenuse AB and its projection AD on the hypotenuse.
$$ \overline{AB} : \overline{AC} = \overline{AC} : \overline{AD} $$
Substituting the corresponding segment lengths:
$$ 5 : 2.2361 = 2.2361 : 1 $$
In the proportion, the length of the leg (2.2361) is the geometric mean.
The proportion is satisfied, with minor inaccuracies due to rounding off decimal figures for side AC by GeoGebra.
$$ 2.2361 = 2.2361 $$
The same holds true for the other leg BC of the right triangle.
Despite minor rounding inaccuracies due to GeoGebra, the example demonstrates the validity of the corollary using actual measurements.
The Proof
Consider the right triangle ABC and leg AC.
The segment AH is the projection of leg AC onto the hypotenuse AB.
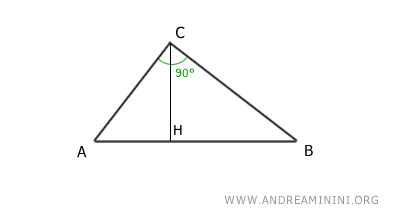
By the first criterion of triangle similarity, triangles ABC and AHC are similar because they have two congruent angles in the same order: a right angle (90°) and a coincident angle (α).
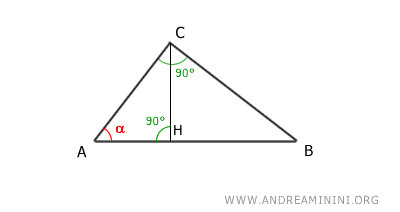
Note. If the triangles have two congruent angles, then the third angle is also congruent, as the sum of the interior angles of a triangle is always 180°.
Therefore, triangles ABC and AHC are similar.
$$ ABC \approx AHC $$
Being similar triangles, all corresponding sides are proportionate.
$$ \overline{AB} : \overline{AC} = \overline{AC} : \overline{AH} = \overline{CB} : \overline{CH} $$
This proves the corollary: the hypotenuse (AB) is to the leg (AC) as the leg (AC) is to its projection (AH) on the hypotenuse.
$$ \overline{AB} : \overline{AC} = \overline{AC} : \overline{AH} $$
And so on.
