Height of a Triangle
The height (h) of a triangle is a perpendicular segment that connects a vertex to the opposite side or its extension.
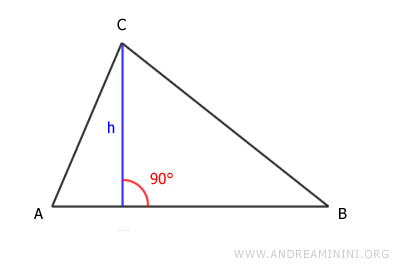
In other words, it is the perpendicular distance from a vertex to the chosen base.
The height forms two right angles with the base.
Since a triangle has three sides and any side can be chosen as the base, a triangle always has three heights.
For example, if we choose side CB as the base, the height is as follows:
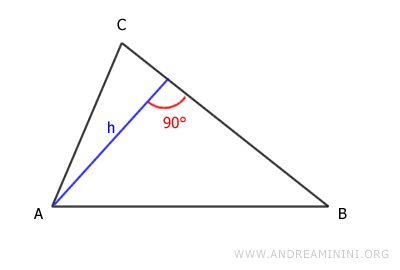
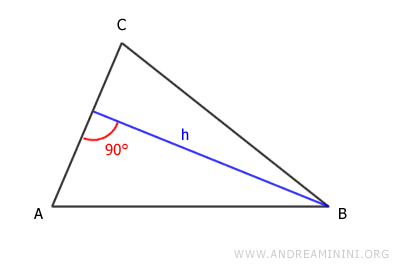
If we choose side AC as the base, the height is as follows:
The height (h) can also be a segment outside the triangle because in some cases it is perpendicular to an extension of the base.
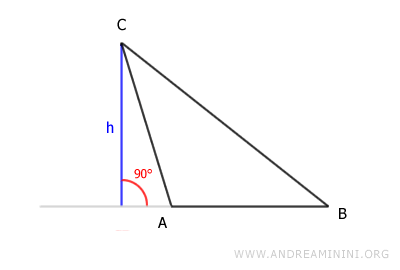
This aspect distinguishes the height from the angle bisector and the median, which are always internal segments of the triangle.
How to Calculate the Height of a Triangle
The formula to find the height of a triangle is as follows:
$$ h = \frac{2A}{b} $$
Where A is the area of the triangle and b is the length of the base.
To calculate the height of the triangle, simply divide twice the area by the length of the base.
Note: This formula is derived from the fact that the area (A) of the triangle is equal to the base times the height divided by two. $$ A = \frac{b \cdot h}{2} $$ Rearranging the formula to solve for h (the height), we multiply both sides by two. $$ 2 \cdot A = 2 \cdot \frac{b \cdot h}{2} $$ $$ 2 \cdot A = b \cdot h $$ We then divide both sides by the base and simplify: $$ \frac{2A}{b} = h $$
A Practical Example
Consider a triangle ABC.
Let's use segment AB as the base.
Draw a segment perpendicular to base AB that passes through the opposite vertex C.
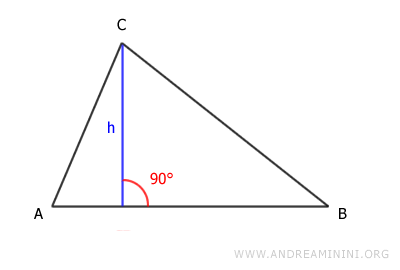
This segment is the height of the triangle.
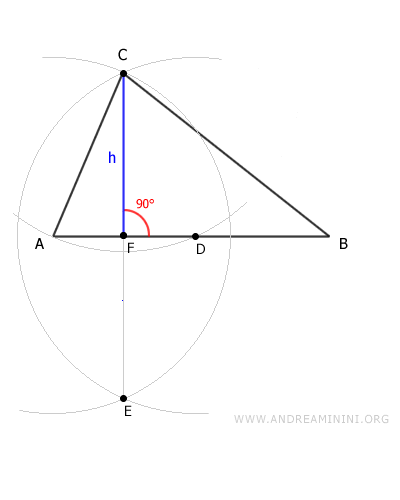
How to Find the Height of a Triangle: To find the height relative to base AB, place the compass point on the opposite vertex C and draw an arc with radius AC to locate point D.
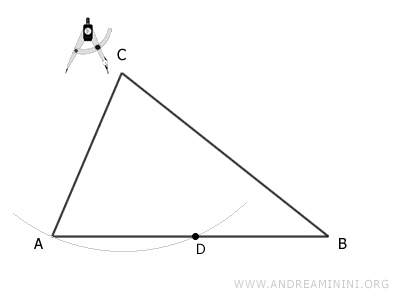
Keeping the same compass width, draw an arc with center A and another arc with center D. The intersection of these two arcs determines point E outside the triangle.
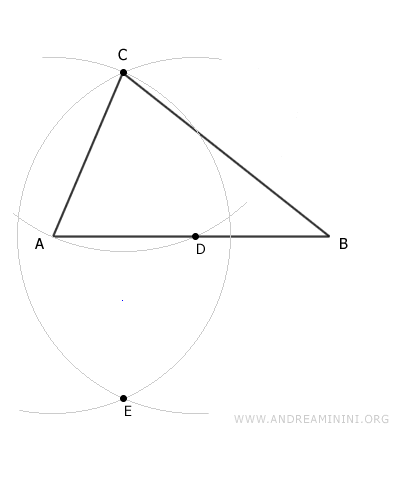
Draw segment EC, which intersects the base at point F. Segment EC is perpendicular to the base, forming a 90-degree angle. The height of the triangle is segment CF.
Height of an Equilateral Triangle
The height of an equilateral triangle can be calculated using the following formula: \[ h = \frac{\sqrt{3}}{2} \cdot l \] where \( h \) is the height and \( l \) is the length of a side of the triangle.
This formula is derived from the geometric properties of an equilateral triangle.
Knowing the length of one side is sufficient to determine the height of the triangle.
Example
Consider an equilateral triangle ABC with all sides of length 6.
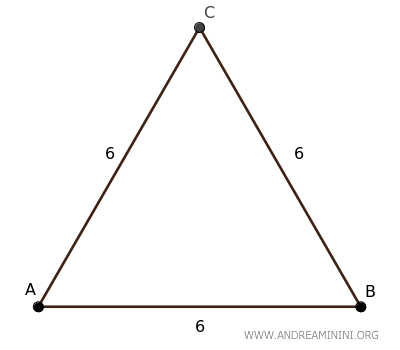
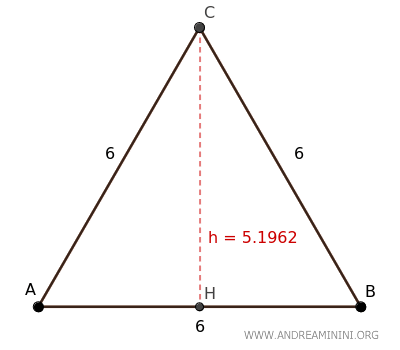
To find the height of this equilateral triangle, we use the formula:
$$ h = \frac{\sqrt{3}}{2} \cdot l $$
Here, \( l = 6 \)
$$ h = \frac{\sqrt{3}}{2} \cdot 6 $$
$$ h = 3 \cdot \sqrt{3} $$
$$ h \approx 5.1962 $$
Thus, the height of the equilateral triangle is approximately 5.1962.
Proof
An equilateral triangle has all three sides of equal length.
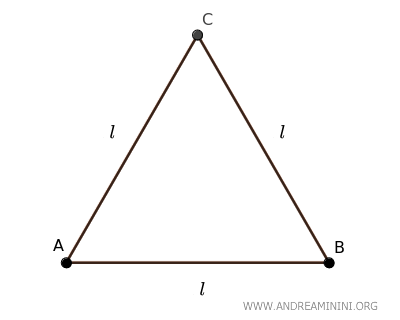
If you draw a height from one of the vertices to the opposite side, it divides the equilateral triangle into two congruent right triangles, \( \triangle ACH \cong \triangle BCH \).
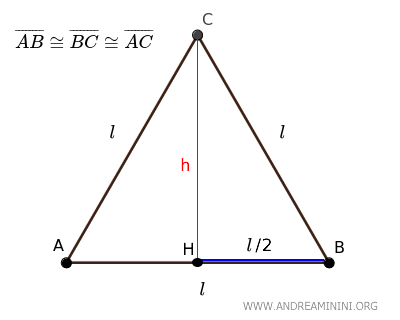
In each right triangle, the height \( h \) is one of the legs, half of the base \( \frac{l}{2} \) is the other leg, and the side of the equilateral triangle \( l \) is the hypotenuse.
To find the length of the leg in the right triangle, we can apply the Pythagorean theorem:
$$ l^2 = h^2 + \left(\frac{l}{2}\right)^2 $$
$$ l^2 = h^2 + \frac{l^2}{4} $$
Solving for the height \( h \):
$$ h^2 = l^2 - \frac{l^2}{4} $$
$$ h^2 = \frac{3l^2}{4} $$
Taking the square root of both sides:
$$ \sqrt{h^2} = \sqrt{\frac{3l^2}{4}} $$
$$ h = \sqrt{\frac{3l^2}{4}} $$
$$ h = \frac{\sqrt{3}}{2} l $$
Therefore, the height \( h \) of an equilateral triangle with side length \( l \) is \(\frac{\sqrt{3}}{2} \times l\).
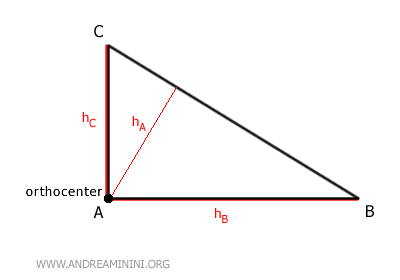
Orthocenter
The orthocenter is the point where the three heights of the triangle intersect.
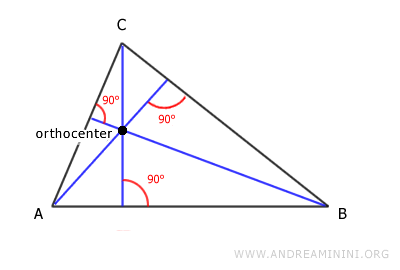
It can be located inside or outside the triangle, or on one of its vertices, depending on the angles:
- Inside the triangle
If the triangle is acute, meaning all three angles are acute, the orthocenter is inside the triangle.
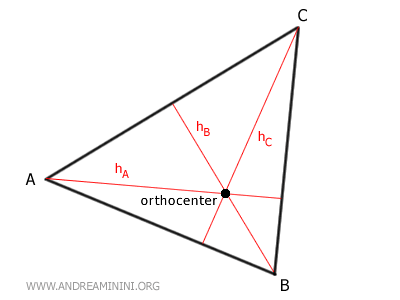
- Outside the triangle
If the triangle is obtuse, meaning one of its angles is obtuse, the orthocenter is outside the triangle.
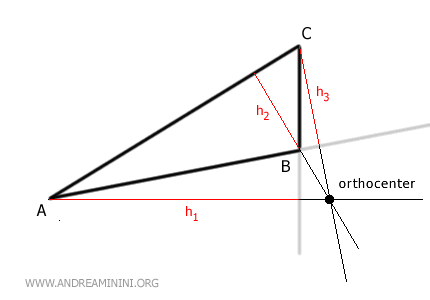
- On one of the vertices
If the triangle is right-angled, meaning one of its angles is 90 degrees, the orthocenter is on the vertex with the right angle.
And so on.
