Theorem of a Line Parallel to a Side of a Triangle
A line parallel to one side of a triangle intersects the other two sides, dividing them into proportional segments.
This theorem originates from the Theorem of Thales.
It states that if a line parallel to one side of a triangle intersects the other two sides, it divides these sides into proportional segments.
This is one of the fundamental concepts of triangle similarity.
The converse of this theorem is also true
If a line intersects two sides of a triangle, dividing them into proportional segments, then this line is parallel to the third side of the triangle.
Therefore, this theorem also serves as a criterion for parallelism in Euclidean geometry. In other words, it provides a method for determining if one line is parallel to another.
Note. This principle is frequently used in plane geometry problems to determine the parallelism of lines and to solve problems involving similar triangles. Additionally, it can be extended to more advanced concepts such as projective geometry and the theory of proportions.
A Practical Example
Consider, for example, a triangle ABC.
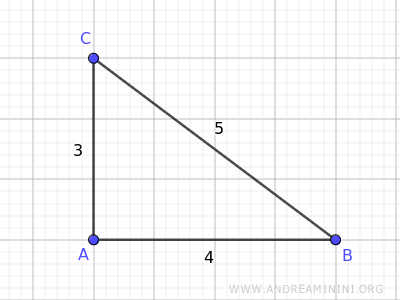
We already know the lengths of the triangle’s sides: AB=4, BC=5, AC=3.
Now, draw a line parallel to side AB that intersects the other two sides of the triangle at points D and E.
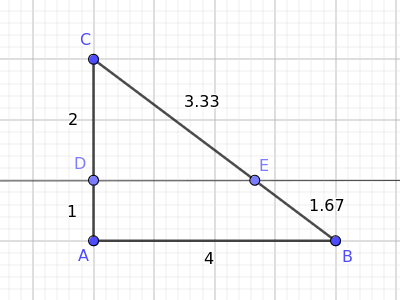
This line intersects sides AC and BC at points D and E, respectively.
- Segment AC is divided into two segments AD and DC, measuring 1 and 2, respectively.
- Segment BC is divided into two segments BE and EC, measuring 1.67 and 3.33, respectively.
The Theorem of Thales states that AD/DC = BE/EC, meaning that the two pairs of segments are directly proportional.
$$ \frac{ \overline{AD} }{ \overline{DC} } = \frac{ \overline{BE} }{ \overline{EC} } $$
Substitute the segment values AD=1, DC=2, BE=1.67, EC=3.33
$$ \frac{ 1 }{ 2 } = \frac{ 1.6\overline{7} }{ 3.\overline{33} } $$
$$ 0.5 = 0.5 $$
The ratio between segments AD/DC and BE/EC is the same.
Thus, the two pairs of segments are directly proportional.
The Proof
The proof of the theorem is quite straightforward.
Consider any triangle ABC.
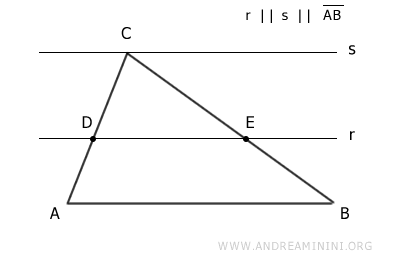
Initially, draw a line parallel to side AB of the triangle that intersects the other two sides at points D and E.
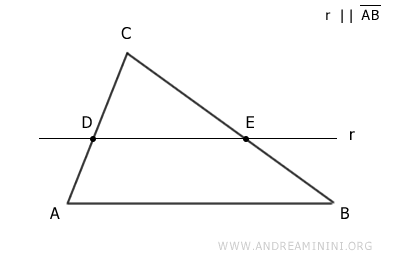
Next, add another line s passing through the vertex opposite side AB of the triangle.
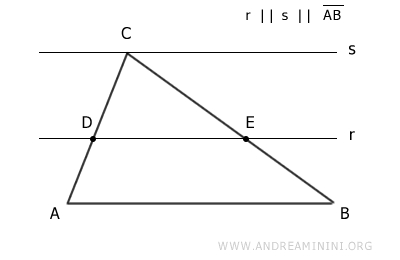
Segment AB and the parallel lines r and s form a bundle of lines cut by the two transversals BC and AC.
According to the Theorem of Thales, sides BC and AC are divided proportionally.
$$ AD:DC = BE:EC $$
Therefore, the two sides are divided proportionally.
Proof of the Converse Theorem
Since the Theorem of Thales also has a converse theorem, we can deduce that the same holds for its corollary.
If, hypothetically, a line divides two sides of a triangle into proportional segments, then we can deduce that this line is parallel to the third side of the triangle.
And so on.
