Obtuse Triangle

An obtuse triangle is a triangle in which one of the internal angles measures more than 90°, making it an obtuse angle.

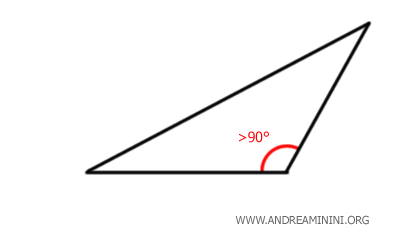
The other two angles are acute because the sum of all angles in a triangle is always 180°.

Thus, if one angle is obtuse (>90°), the other two must be acute (<90°).

Note: Unlike right triangles, obtuse triangles do not have a hypotenuse. Although the side opposite the obtuse angle is longer than the other two sides, it cannot be called the "hypotenuse" because there is no right angle. In other words, only right triangles have a hypotenuse and legs.

Key Points

Here are some important aspects of obtuse triangles:

• The side opposite the obtuse angle is the longest side.

  However, as previously mentioned, it cannot be called the "hypotenuse" because that term is specific to right triangles.

• The sum of its internal angles is always 180°, just like any other triangle.
• An obtuse triangle can be either a scalene triangle or an isosceles triangle.

  However, it cannot be an equilateral triangle because an equilateral triangle has all three angles measuring 60°. Therefore, it cannot be obtuse or right-angled.

• In an obtuse triangle, the sum of the lengths of the two shorter sides is greater than the length of the longest side.
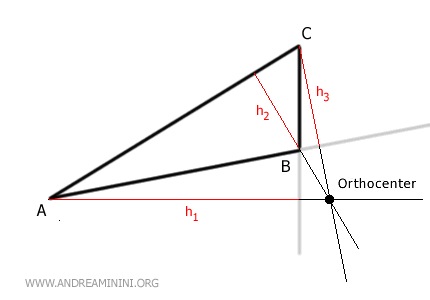
• Orthocenter
  The orthocenter is located outside the obtuse triangle.
  
• Circumcenter
  The circumcenter is also located outside the obtuse triangle.
• Incenter
  The incenter is located inside the obtuse triangle.
• Centroid
  The centroid is a point inside the obtuse triangle.

And so on.