Relationship Between Sides and Opposite Angles in a Triangle

In any triangle, there is a fundamental relationship between its sides and the angles opposite them.

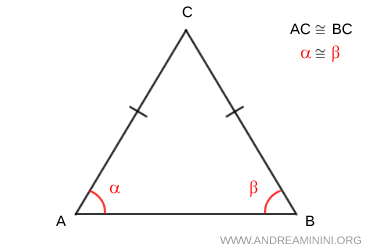
If two sides of a triangle are congruent, then the angles opposite those sides are also congruent. For instance, in an isosceles triangle, the two equal sides correspond to two equal opposite angles.
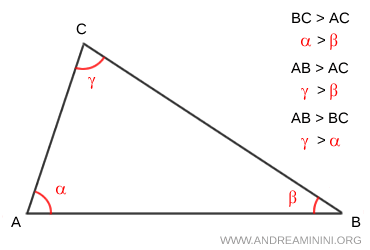
If a triangle has two sides of different lengths, then the opposite angles are also unequal—the longer side is always opposite the larger angle.

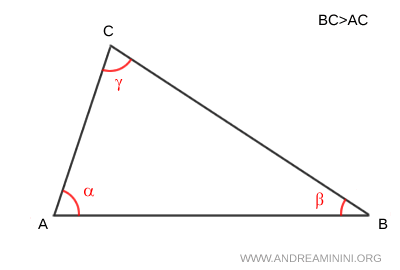
Proof
The Converse Theorem

Proof

Suppose we have a triangle where one side is longer than another.

$$ BC>AC $$

We aim to prove that the angle $ \alpha $ opposite $ BC $ is larger than the angle $ \beta $ opposite $ AC $.

the proof

Since $ BC $ is longer than $ AC $, there must exist a point $ P $ on segment $ BC $ such that $ AB \cong CP $.

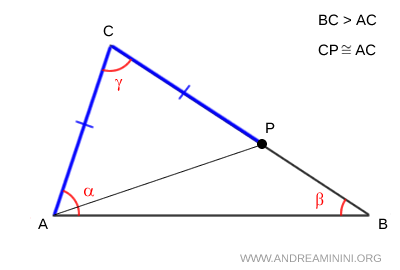
example

By construction, $ \triangle ACP $ is isosceles, as it has two equal sides, $ AB \cong CP $. This implies that its base angles, denoted as $ \theta $, are also congruent.

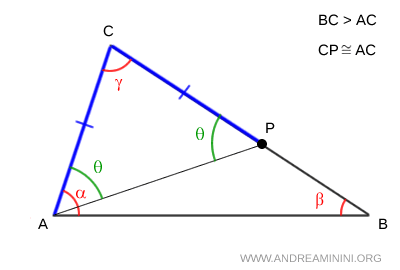
example

Since segment $ AP $ divides angle $ \alpha $, it follows that $ \alpha $ is greater than $ \theta $.

$$ \alpha > \theta $$

Now, considering $ \triangle APC $, we observe that $ \theta $ also serves as an exterior angle.

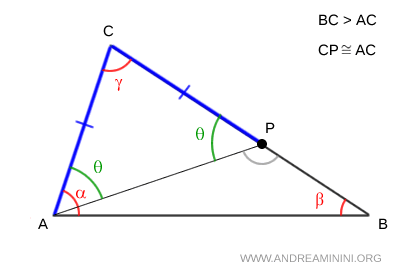
example

By the Exterior Angle Theorem, in any triangle, an exterior angle is always greater than either of the two non-adjacent interior angles.

Thus, we conclude that $ \theta $ is greater than $ \beta $.

$$ \theta > \beta $$

Summing up, we have established the following inequality:

$$ \alpha > \theta > \beta $$

where $ \alpha $ is the angle opposite the longer side $ BC $, and $ \beta $ is the angle opposite the shorter side $ AC $.

Therefore, we have proven that in any triangle, the larger side is always opposite the larger angle.

The Converse Theorem

In a triangle, if two angles are not congruent, then the side opposite the larger angle is always longer than the side opposite the smaller angle.

This leads to some important conclusions:

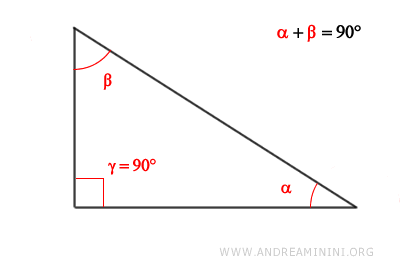
In a right triangle, the hypotenuse is always the longest side because it lies opposite the right angle (90°), which is the largest angle in the triangle.
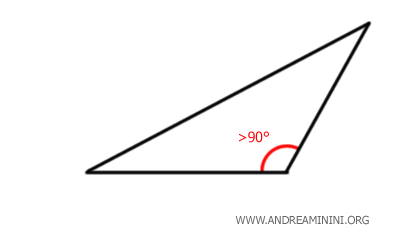
In an obtuse triangle, the side opposite the obtuse angle (greater than 90°) is always longer than either of the other two sides.

And this pattern holds true in all cases.