Right Triangle with 45° Angles

A right triangle with 45° acute angles has two equal-length sides (the legs) because it is also isosceles.

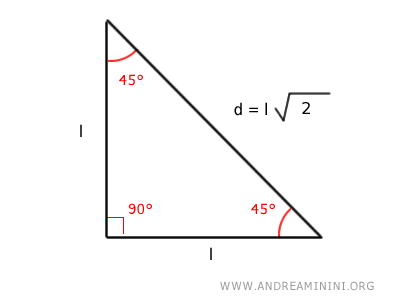
In this triangle, the hypotenuse opposite the right angle is calculated using the formula $$ d = l \cdot \sqrt{2} $$ The sides adjacent to the right angle are congruent.

Explanation

This specific type of right triangle is also known as an "isosceles right triangle."

The two acute angles of the right triangle adjacent to the hypotenuse (a) are congruent, both measuring 45°. Therefore, it is an isosceles triangle.

This means the two legs are congruent b ≅ c, or in other words, they are of equal length, making the triangle symmetrical with respect to the hypotenuse.

 

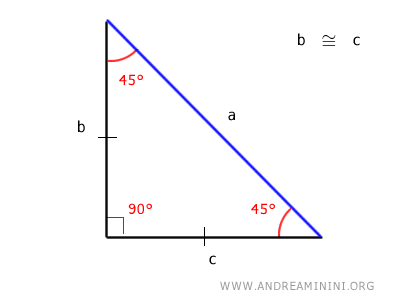
In fact, if you double the triangle, you'll immediately see that it forms a square.

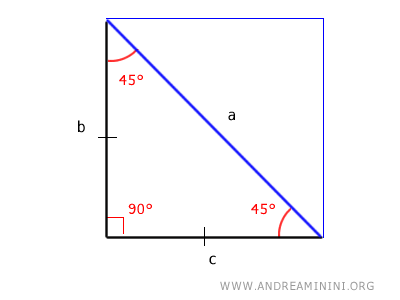
Thanks to this special property, you can calculate the length of all sides knowing just one side.

$$ c = \frac{a}{ \sqrt{2} } = \frac{a}{2} \sqrt{2} $$

$$ a = c \cdot \sqrt{2} $$

It's important to note that these formulas apply only to triangles with two 45° angles.

Another interesting property of the isosceles right triangle is that if you draw an altitude from the hypotenuse to the opposite vertex (the right angle), it divides the hypotenuse into two equal segments and creates two smaller right triangles, both with 45° angles.

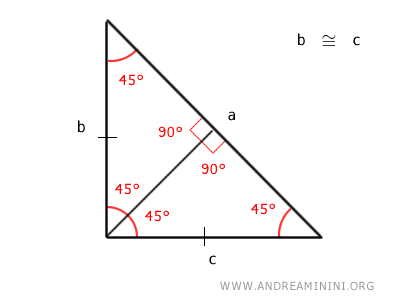
Proof

Consider a right triangle with two 45° angles.

The angles adjacent to side "a" are congruent, making the right triangle isosceles, meaning it has two congruent sides.

Knowing that side "a" is the base of the isosceles triangle, the other two sides must be congruent.

$$ b \cong c $$

Since b=c, we can represent both legs with a single letter, for example, "c."

 

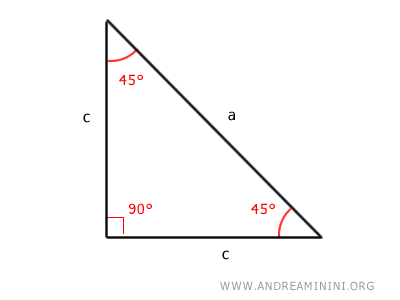
According to the Pythagorean theorem, in a right triangle, the square of the hypotenuse (a²) is equal to the sum of the squares of the legs (c² + c²).

$$ a^2 = c^2 + c^2 $$

$$ a^2 = 2c^2 $$

This relationship allows us to calculate the length of the hypotenuse (a) if we know the length of one leg (c).

$$ a^2 = 2c^2 $$

$$ \sqrt{a^2} = \sqrt{2c^2} $$

$$ a = c \cdot \sqrt{2} $$

If the length of the hypotenuse (a) is known, we can calculate the length of the legs (c).

$$ a^2 = 2c^2 $$

$$ \frac{a^2}{2} = c^2 $$

$$ \sqrt{\frac{a^2}{2}} = \sqrt{c^2} $$

$$ a \cdot \frac{1}{\sqrt{2}} = c $$

$$ c = \frac{a}{\sqrt{2}} $$

By the invariant property of fractions, multiply the numerator and the denominator by the square root of 2.

$$ c = \frac{a \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} $$

$$ c = \frac{a}{2} \sqrt{2} $$

And so on.