Scalene Triangle

A triangle is called a scalene triangle if all three sides have different lengths, or equivalently, if all three angles are different.

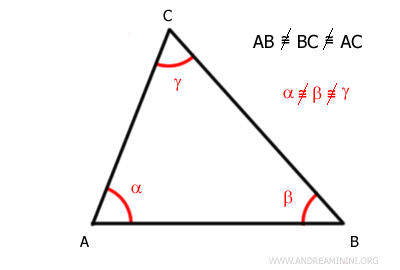
In other words, the sides of a scalene triangle are all of different lengths.

As a result, all three angles are also different.

Note: Generally, when people refer to "triangles" without specifying a type, they mean any kind of triangle. Scalene triangles represent the most general form. Therefore, when discussing triangles in general, it’s useful to consider a scalene triangle.

A Practical Example

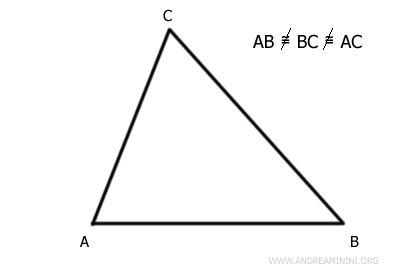
Let’s consider a triangle ABC.

The three sides AB, BC, and AC are not congruent, meaning they have different lengths.

Therefore, the three angles are also not congruent.

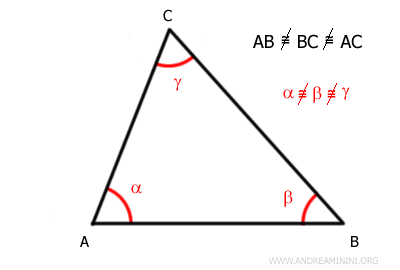
From this, we can deduce that it is a scalene triangle.

Types of Scalene Triangles

There are three types of scalene triangles:

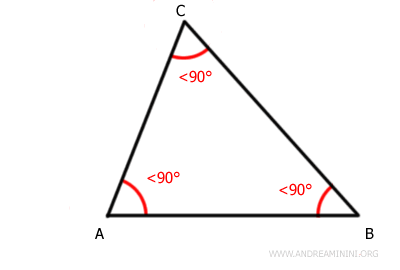
• Acute Scalene Triangle
  It has three sides of different lengths and three angles of different measures. All angles are acute. It is a subset of acute triangles.
  
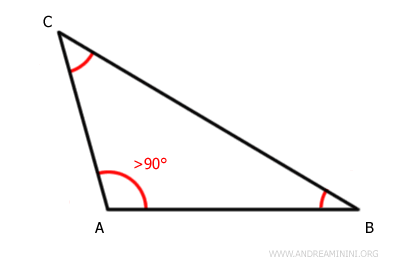
• Obtuse Scalene Triangle
  It has three sides of different lengths and three non-congruent angles. One angle is obtuse, meaning it is greater than 90°. It is a subset of obtuse triangles.
  
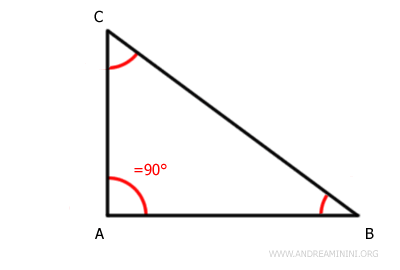
• Right Scalene Triangle
  It has three sides of different lengths and three angles of different measures. Additionally, it has a right angle, which is equal to 90°. It is a subset of right triangles.
  

Properties

Here are some properties of scalene triangles as listed on the YouMath website:

• Convexity
  Every scalene triangle is a convex polygon.
• Sum of Interior Angles
  The sum of the interior angles of a scalene triangle is 180° (π). This is a common characteristic of triangles in Euclidean geometry.
• Sum of Exterior Angles
  The sum of the exterior angles of a scalene triangle is 360° (2π).
• Relationship Between Angles and Sides
  The side opposite the largest interior angle is the longest side. Conversely, the side opposite the smallest interior angle is the shortest side of the triangle.
• Triangle Inequality
  The length of any side is less than the sum of the other two sides.

These properties apply to any type of scalene triangle, regardless of its classification based on angles (acute, obtuse, right).

And so on.