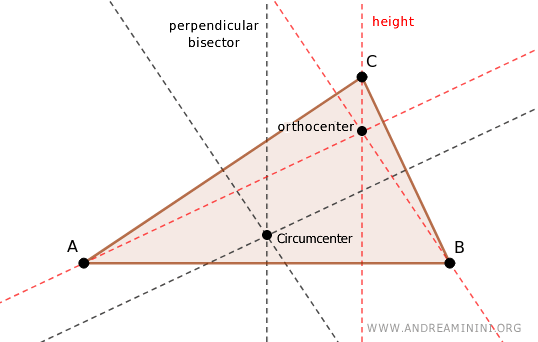
Orthocenter
In a triangle, the orthocenter is the point where its three altitudes intersect.
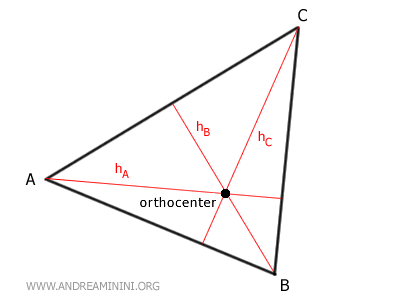
An altitude is a line perpendicular to a side of the triangle, or its extension, passing through the opposite vertex.
Every triangle has three altitudes because it has three vertices and three sides.
The point where these three lines intersect is the orthocenter.
The Position of the Orthocenter
The position of the orthocenter depends on the angles of the triangle.
The orthocenter of a triangle can be located:
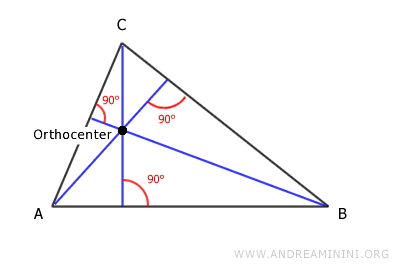
- Inside the triangle if it is acute. If all three angles of the triangle are acute (<90°), the orthocenter is inside the triangle.
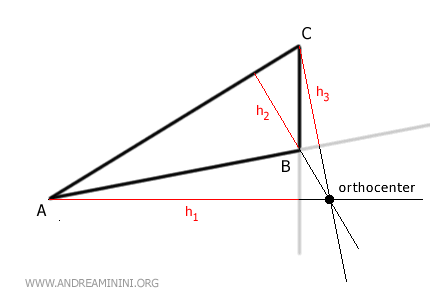
- Outside the triangle if it is an obtuse triangle. If one of the triangle's angles is obtuse (>90°), the orthocenter is outside the triangle.
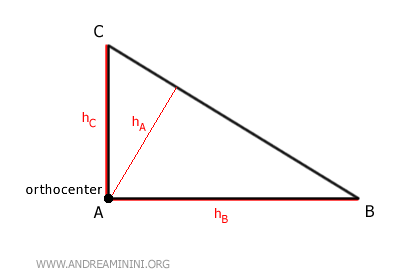
- At one of the triangle's vertices if it is a right triangle. In a right triangle, the orthocenter is located at the vertex of the right angle (90°).
The Proof
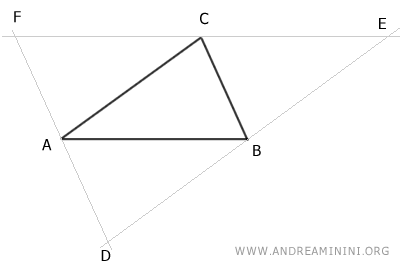
To prove that the altitudes intersect at a common point, consider a triangle ABC.
Draw lines parallel to the sides of the triangle passing through the opposite vertex.
These lines, parallel to the sides, intersect at points D, E, and F.
From this construction, we observe that:
- The segments AD||BC and AC||DB are parallel, forming the parallelogram ADBC.
- The segments AF||BC and AB||CF are parallel, forming the parallelogram ABCF.
As parallelograms, they have congruent opposite sides: AD≅BC, AB≅DB, AF≅BC, AB≅CF.
By the transitive property, since AD≅BC and AF≅BC, we deduce that AD≅AF.
$$ \overline{AD} \cong \overline{AF} $$
Therefore, point A is the midpoint of side DF.
Next, draw the altitude AG of triangle ABC, perpendicular to side BC and passing through vertex A.
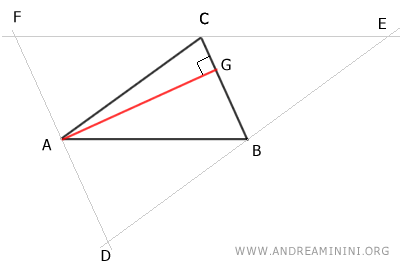
The line containing segment AG is also perpendicular to side DF because DF is parallel to side BC by construction.
Thus, the line containing segment AG (altitude of triangle ABC) is the axis of triangle DEF because it is perpendicular to side DF and passes through its midpoint A.
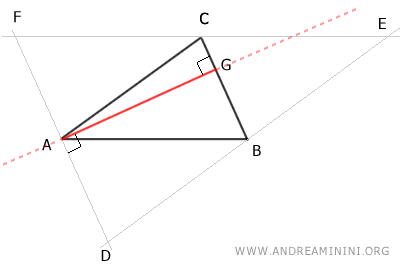
Similarly, I can prove that point B is the midpoint of segment DE.
By construction, there are two parallelograms, ADBC and ABEC, with congruent opposite sides.
By the transitive property, if DB≅AC and BE≅AC, we deduce that DB≅BE.
$$ \overline{DB} \cong \overline{BE} $$
Therefore, point B is the midpoint of segment DE.
Next, draw the altitude BH of triangle ABC, perpendicular to side AC and passing through vertex B.
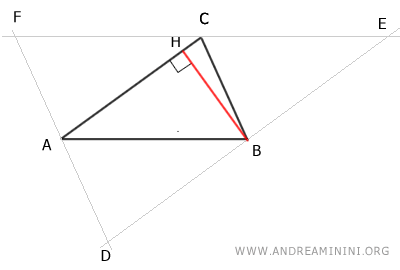
Knowing that AC||DE are parallel by construction, the line containing segment BH is also perpendicular to side DE.
Thus, the altitude BH of triangle ABC coincides with the axis of side DE of triangle DEF.
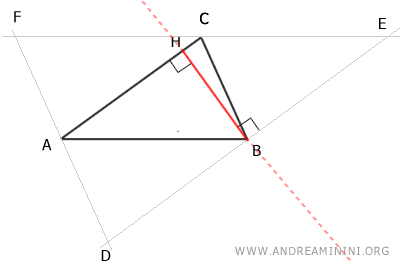
Finally, using the same procedure, I demonstrate that point C is the midpoint of segment EF.
By construction, there are two parallelograms, ABCF and ABEC, with congruent opposite sides.
By the transitive property, if AB≅CF and AB≅CE, we deduce that CF≅CE.
$$ \overline{CF} \cong \overline{CE} $$
Therefore, if CF≅CE, then point C is the midpoint of segment EF.
Next, draw the altitude IC of triangle ABC, perpendicular to side AB and passing through vertex C.
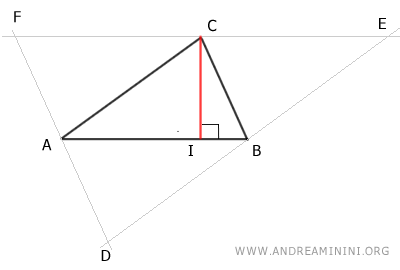
Knowing that AB||EF are parallel by construction, we deduce that the line containing segment IC is also perpendicular to side EF.
Thus, the altitude IC of triangle ABC coincides with the axis of side EF of triangle DEF.
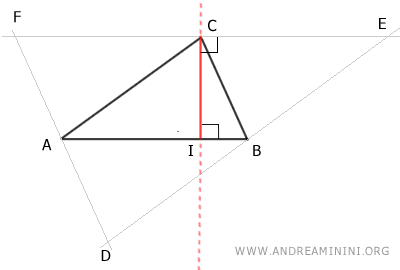
So far, I have demonstrated that the altitudes of triangle ABC are segments included in the axes of triangle DEF.
In conclusion, knowing that the axes of a triangle always intersect at a common point (see circumcenter proof), we deduce that the lines containing the altitudes of a triangle intersect at a common point.
In other words, the lines that include the altitudes of a triangle are parallel to the axes of the same triangle because they are perpendicular to the same side.
Parallel lines to intersecting lines are also intersecting lines.
Therefore, once it is proven that the axes of the triangle always intersect at a common point (circumcenter), we can deduce that the lines containing the altitudes of the triangle intersect at a common point (orthocenter).
And so on.
