Angle Bisector Theorem for an Interior Angle of a Triangle
The bisector of an interior angle of a triangle divides the opposite side into two segments that are directly proportional to the other two sides of the triangle. $$ \overline{BD} : \overline{CD} = \overline{AB} : \overline{AC} $$ 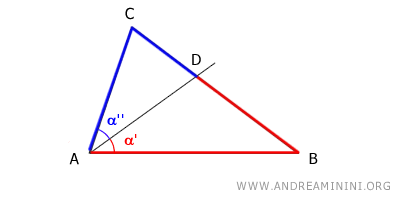
In other words, if you have a triangle ABC with an angle bisector starting from angle A and intersecting the opposite side BC at point D, the length of segment BD is proportional to the length of segment CD. This proportion is equal to the proportion of the lengths of the sides adjacent to the triangle, i.e., AB/AC.
Mathematically, this can be expressed as:
$$ \overline{AB} : \overline{AC} = \overline{BD} : \overline{CD} $$
which can also be written as:
$$ \frac{\overline{AB}}{\overline{AC}} = \frac{\overline{BD}}{\overline{CD}} $$
This theorem is useful in many geometric applications and can help solve problems related to triangles when some side lengths or angles are known.
The converse theorem also holds: If a point divides a side of a triangle into two segments proportional to the other two sides of the triangle, then the segment joining the point to the opposite vertex of the triangle is the bisector of the vertex angle.
A Practical Example
Consider a triangle with sides of lengths AB=4, BC=5, and AC=3.
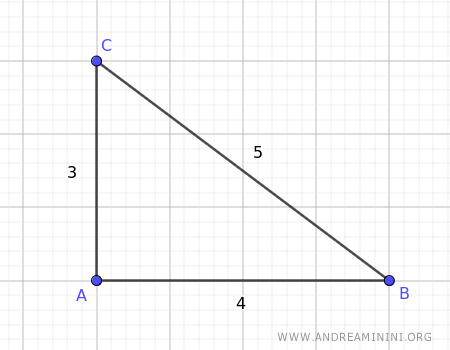
Draw the angle bisector from vertex A.
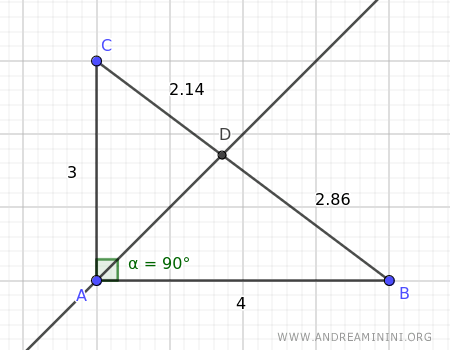
The angle bisector of $ \hat{A} $ divides the opposite side $ \overline{BC} $ into two segments, BD=2.86 and CD=2.14.
The ratio between segments BD and CD is approximately 1.34:
$$ \frac{\overline{BD}}{\overline{CD}} = \frac{2.86}{2.14} = 1.33 $$
Now, I check if these two segments are proportional to the other two sides, AB and AC, of the triangle.
$$ \frac{\overline{AB}}{\overline{AC}} = \frac{4}{3} = 1.33 $$
The ratio is the same, so segments BD and CD are directly proportional to sides AB and AC of triangle ABC.
The Proof
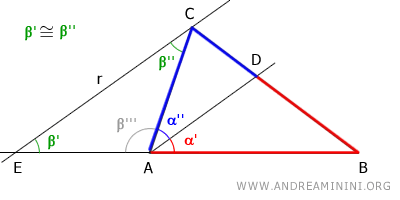
Consider any triangle ABC.
Draw the angle bisector of $ \hat{A} $, which intersects the opposite side BC at point D, dividing it into two segments, BD and CD.
The angle bisector divides angle A into two equal angles, α'≅α'' (congruent).
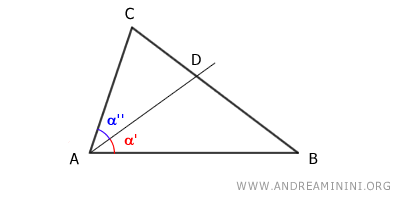
I need to prove that segment BD is to CD as AB is to AC:
$$ BD : CD = AB : AC $$
In other words, I need to show that BD and CD are directly proportional to AB and AC.
Draw a line r parallel to the bisector passing through vertex C.
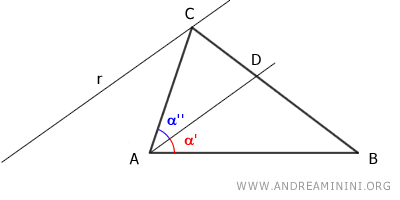
Extend side BA until it intersects line r at point E.
This forms a triangle EAC with angles β', β'', β''' and a larger triangle EBC.
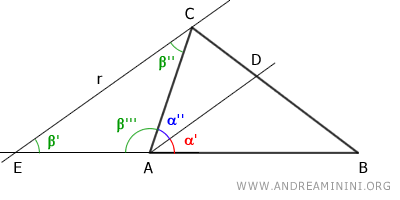
Line AD is parallel to side EC of triangle EBC, so it divides the other two sides of triangle EBC into proportional segments according to the theorem of the line parallel to the side of a triangle.
$$ BD : CD = AB : AE $$
Angles α'' and β'' are alternate interior angles of two parallel lines cut by a transversal AC, so according to the theorem of parallel lines, they are congruent: α''≡β''
$$ \alpha '' \cong \beta '' $$
Angles α' and β' are corresponding angles of two parallel lines cut by a transversal AC, so again according to the theorem of parallel lines, they are congruent: α'≡β'
$$ \alpha ' \cong \beta ' $$
Knowing that the angle bisector AC of triangle ABC divides angle A into two congruent angles, α'≅α'', I deduce by the triangle congruence that β'≅β'' are also congruent.
$$ \beta ' \cong \beta '' $$
Therefore, triangle EAC is an isosceles triangle with base EC, because it has two congruent angles, β'≅β''.
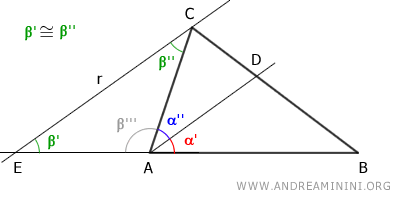
Knowing that EAC is an isosceles triangle, I deduce that it has congruent sides, EA≅AC.
$$ \overline{EA} \cong \overline{AC} $$
Now I return to the proportion in triangle EAC:
$$ BD : CD = AB : AE $$
Since EA≅AC, I replace AE with AC:
$$ BD : CD = AB : AC $$
This proves the initial proportion.
Thus, the segments BD and CD, obtained by dividing side BC with the angle bisector from vertex A, are directly proportional to the other sides AB and AC of triangle ABC.
Note: Since the theorem of the line parallel to the side of a triangle derives from Thales' theorem, it follows that this angle bisector theorem is also a corollary of Thales' theorem.
And so on.
