Heron's Formula

Ever wondered how to find the area of a triangle when all you know are its side lengths? Heron's formula is your mathematical go-to! It's elegantly simple: $$ A = \sqrt{p(p-a)(p-b)(p-c)} $$ Here, $a$, $b$, and $c$ are the sides of the triangle, and $p$ stands for the semiperimeter of the triangle.

Now, the semiperimeter might sound fancy, but it's just the half of the triangle's perimeter:

$$ p= \frac{a+b+c}{2} $$

What makes Heron's formula super handy is its independence from the triangle's height or angles, allowing for a straightforward area calculation.

Basically, it's a real lifesaver when measuring the height feels like solving another puzzle.

Heads up: Credit where credit’s due – this formula was named after Hero of Alexandria, an ingenious Greek mathematician and engineer from the 1st century AD. Chances are, though, this mathematical gem was discovered even before his time.

Don't worry about your triangle being of a specific type; Heron's formula isn't picky. Whether it’s scalene, isosceles, or equilateral, as long as you know the side lengths, you’re all set.

Putting It to the Test

Let’s break it down with a triangle whose sides are 8, 15, and 17 units long.

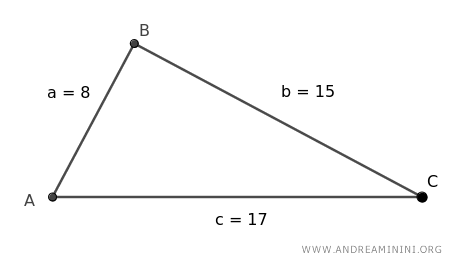
triangle example

Our mission: Find this triangle's area.

Since the height is MIA, the classic base times height formula won’t cut it.

$$ A = \frac{ \text{base} \ × \ \text{height} }{2} $$

But no stress, we've got all sides of the triangle accounted for.

That’s our cue to apply Heron's formula.

$$ A = \sqrt{p(p-a)(p-b)(p-c)} $$

With $a$, $b$, and $c$ as our side lengths and $p$ as our trusty semiperimeter.

Plugging in the numbers: a=8, b=15, and c=17.

\[A = \sqrt{p(p - 8)(p - 15)(p - 17)}\]

Next up, calculating the semiperimeter $p$ – just add up the side lengths and divide by two.

$$ p = \frac{a + b + c}{2} $$

$$ p = \frac{8 + 15 + 17}{2} = 40/2 = 20 $$

Fun fact: Why bother with a semiperimeter? It’s kind of the middle ground that ties the side lengths to the area, balancing everything out.

With $ p = 20 $, let’s finalize our area calculation:

$$ A = \sqrt{20(20 - 8)(20 - 15)(20 - 17)} $$

$$ A = \sqrt{20 \times 12 \times 5 \times 3} = \sqrt{3600} = 60 $$

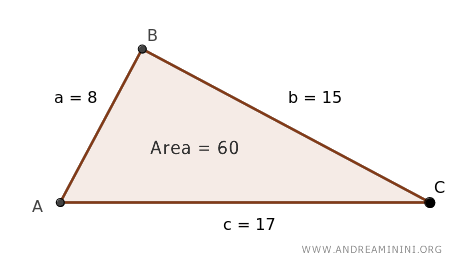
Voilà, the triangle with sides of 8, 15, and 17 units squares up to 60 square units in area.

A quick check with Geogebra confirms we’re on the mark.

triangle area is A=60

Did you know? The square root in Heron's formula isn’t just for show. It's the magic touch that normalizes the mix of the semiperimeter and side length differences, giving us the area.

And that’s a wrap!