Calculating the Area of a Triangle Using Trigonometry

The area of a triangle is equal to half the product of two sides l₁ and l₂, and the sine of the angle (α) between them. $$ Area = \frac{1}{2} \cdot (l_1 \cdot l_2) \cdot \sin \alpha $$

Here, l₁ and l₂ are two adjacent sides of the triangle, and α is the angle between these sides.

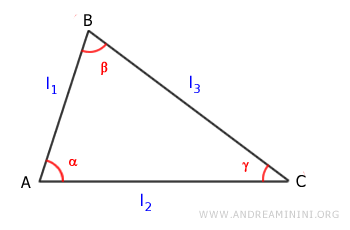
Similarly, the following formulas are also valid:

$$ Area = \frac{1}{2} \cdot (l_1 \cdot l_3) \cdot \sin \beta $$

$$ Area = \frac{1}{2} \cdot (l_2 \cdot l_3) \cdot \sin \gamma $$

These formulas can be applied to any type of triangle (isosceles, right, scalene).

A Practical Example

Let's consider a right triangle.

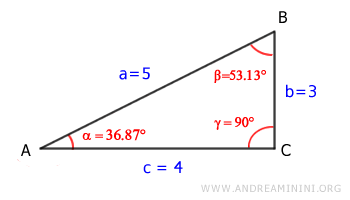
The area of the triangle is base (c) times height (b) divided by two.

$$ Area = \frac{1}{2} (c \cdot b) = \frac{1}{2} (4 \cdot 3) = 6 $$

Now, let's calculate the area using trigonometry.

We'll consider the adjacent sides a = 5, c = 4 and the included angle α = 36.87°.

$$ Area = \frac{1}{2} (a \cdot c) \sin \alpha $$

$$ Area = \frac{1}{2} (5 \cdot 4) \sin 36.87° $$

$$ Area = \frac{1}{2} (20) \cdot 0.6 $$

$$ Area = 6 $$

The result is the same.

Furthermore, if we consider the adjacent sides a = 5, b = 3 and the included angle β = 53.13°, we get the same result.

$$ Area = \frac{1}{2} (a \cdot b) \sin \beta $$

$$ Area = \frac{1}{2} (5 \cdot 3) \sin 53.13° $$

$$ Area = \frac{1}{2} (15) \cdot 0.8 $$

$$ Area = 6 $$

Similarly, considering the adjacent sides c = 4, b = 3 and the included angle γ = 90°, the result remains the same.

$$ Area = \frac{1}{2} (c \cdot b) \sin \gamma $$

$$ Area = \frac{1}{2} (4 \cdot 3) \sin 90° $$

$$ Area = \frac{1}{2} (12) \cdot 1 $$

$$ Area = 6 $$

In every case, the area of the triangle is 6.

Example 2

In this example, we consider an isosceles triangle.

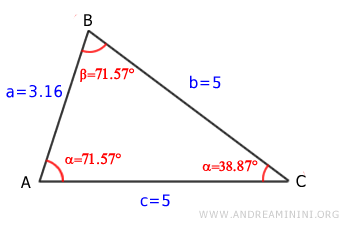
We calculate the area using sides b = 5 and c = 5, and the included angle γ = 36.87°.

$$ Area = \frac{1}{2} (b \cdot c) \sin \gamma $$

$$ Area = \frac{1}{2} (5 \cdot 5) \sin 36.87° $$

$$ Area = \frac{1}{2} (25) \cdot 0.6 $$

$$ Area = 7.5 $$

Alternatively, we can calculate the area using sides a = 3.16 and c = 5, and the included angle α = 71.57°.

$$ Area = \frac{1}{2} (a \cdot c) \sin \alpha $$

$$ Area = \frac{1}{2} (3.16 \cdot 5) \sin 71.57° $$

$$ Area = 7.5 $$

Or using sides a = 3.16 and b = 5, and the included angle β = 71.57°.

$$ Area = \frac{1}{2} (3.16 \cdot 5) \sin 71.57° $$

$$ Area = 7.5 $$

In every case, the result is always the same.

The area of the triangle is 7.5.

The Proof

Case 1

Let's consider a right triangle.

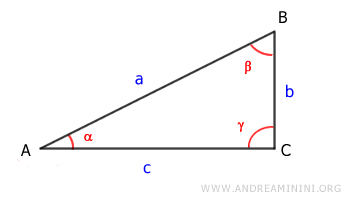
The area of a triangle is base (c) times height (b) divided by two.

$$ Area = \frac{1}{2} \cdot c \cdot b $$

According to the first theorem of right triangles, the length of leg b (height) is equal to the hypotenuse (a) times the sine of the opposite angle (α), i.e., b = a \sin \alpha

$$ Area = \frac{1}{2} \cdot c \cdot (a \cdot \sin \alpha) $$

$$ Area = \frac{1}{2} \cdot (c \cdot a) \cdot \sin \alpha $$

Here, the angle α is the angle between sides a and c of the triangle.

This gives us the formula we set out to prove.

Case 2

Let's consider an isosceles triangle with sides b = c and congruent angles α = β.

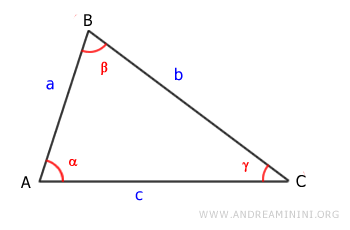
We draw the height (h) of the triangle, which is the segment BD.

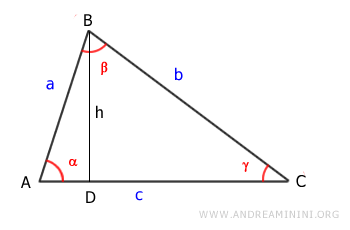
The area of the triangle is base (c) times height (h) divided by two.

$$ Area = \frac{1}{2} \cdot c \cdot h $$

The height (h) is the leg of the right triangle ABD.

According to the first theorem of right triangles, the length of segment BD (the height h) is equal to the hypotenuse (AB) times the sine of the opposite angle (α), i.e., h = a \sin \alpha

$$ Area = \frac{1}{2} \cdot c \cdot a \cdot \sin \alpha $$

Here, the acute angle α is the angle between sides a and c of the isosceles triangle.

This again gives us the formula we set out to prove.

Case 3

Let's consider a scalene triangle with an obtuse angle (α).

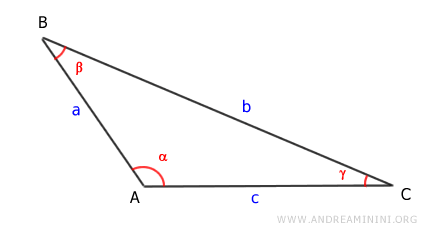
We draw the height (h) of the triangle, which is the segment AD.

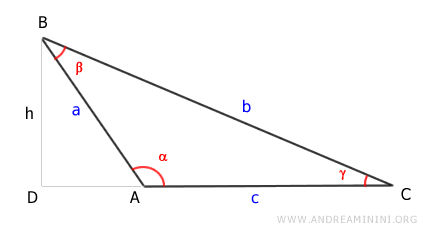
The area of the triangle is base (c) times height (h) divided by two.

$$ Area = \frac{1}{2} \cdot c \cdot h $$

The height h is the leg AD of the right triangle ADB.

According to the first theorem of right triangles, the length of segment BD (the height h) is equal to the hypotenuse (AB) times the sine of the opposite angle (π-α), i.e., h = a \sin (\pi - \alpha)

 

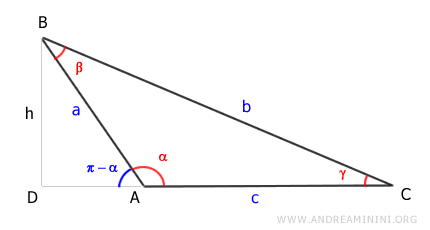
We replace h with a \sin(π-α).

$$ Area = \frac{1}{2} \cdot c \cdot h $$

$$ Area = \frac{1}{2} \cdot c \cdot a \cdot \sin (\pi - \alpha) $$

The opposite angle (π-α) is the supplementary angle of the obtuse angle α.

Knowing that for the property of associated angles, the equality \sin(\pi - \alpha) = \sin(\alpha) holds, we can rewrite the formula in this equivalent form:

$$ Area = \frac{1}{2} \cdot c \cdot a \cdot \sin (\alpha) $$

Here, the obtuse angle α is the angle between sides a and c of the scalene triangle.

This way, we again obtain the formula we set out to prove.

In conclusion, the formula for calculating the area is valid for any type of triangle.

And so on.