Secant
What is the Secant?
In trigonometry, the secant is a function that associates an angle α with the reciprocal of the cosine. It is denoted as sec and is expressed as: $$ \sec \alpha = \frac{1}{\cos \alpha} $$
Geometrically, the secant (OB) is the point where the line (r), which is tangent at point P on the unit circle, intersects the x-axis.
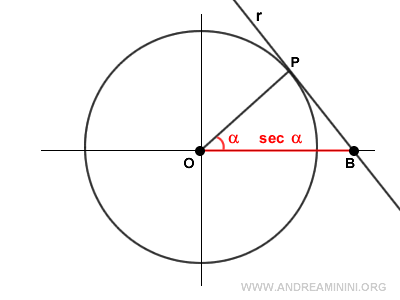
The secant can also be seen as the line segment OC that starts at the origin O, passes through point P, and intersects the tangent at point C.
The secant function is defined for all real numbers except at points π/2 + kπ, where k is an integer and the cosine is zero.
$$ \sec \alpha \ : \ R - \frac{\pi}{2}+k \cdot \pi \rightarrow R - (-1,1) \ \ \ \ \ \ \ \ k \in Z $$
The codomain is the set of real numbers excluding the interval (-1, 1).
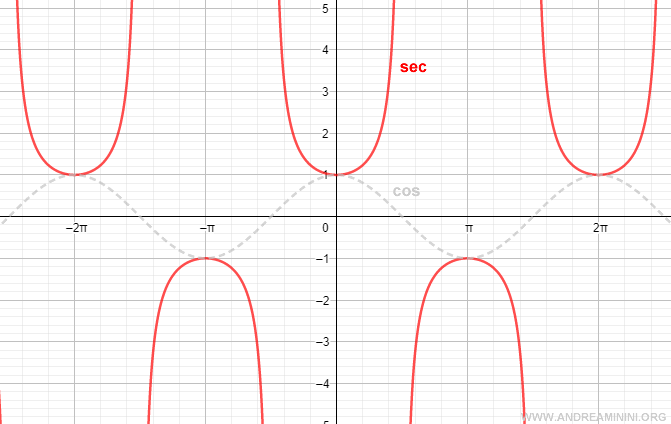
Mathematically, the secant is classified as an even function since f(x) = f(-x).
It is also a periodic function and can be studied within the interval (0, 2π).
Note: The secant function is undefined at points π/2 + kπ for any integer k. At these points, a vertical asymptote is present.
Here are some key values of the secant that are worth memorizing:
| Degrees | Radians | Secant |
|---|---|---|
| 0° | 0 | 1 |
| 45° | π/4 | √2 |
| 60° | π/3 | 2 |
| 90° | π/2 | undefined |
| 120° | 2π/3 | -2 |
| 180° | π | -1 |
| 270° | 3π/2 | undefined |
| 360° | 2π | 1 |
Proof
The triangle OAC is similar to triangle ODP.
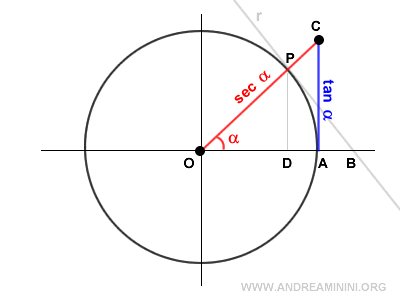
Therefore, we can establish the following proportion:
$$ \overline{OP} \ : \overline{OD} = \overline{OC} \ : \overline{OA} $$
or
$$ \frac{ \overline{OP} } { \overline{OD} } = \frac{ \overline{OC} } { \overline{OA} } $$
The segment OD represents the cosine of angle α:
$$ \frac{ \overline{OP} } { \cos \alpha } = \frac{ \overline{OC} } { \overline{OA} } $$
Since the radius of the unit circle is 1, we substitute OA = 1 and OP = 1:
$$ \frac{ 1 } { \cos \alpha } = \frac{ \overline{OC} } { 1 } $$
$$ \frac{ 1 } { \cos \alpha } = \overline{OC} $$
Thus, the segment OC is the secant of angle α:
$$ \frac{ 1 } { \cos \alpha } = \sec \alpha $$
This is how we derive the formula for the secant as the reciprocal of the cosine.
Alternative Proof: The triangles OPB and OPD are similar since they have identical angles.
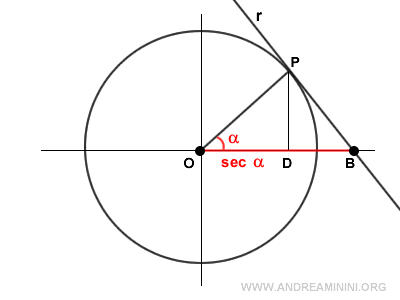
Therefore, they maintain the same ratio between the side and the hypotenuse: $$ \frac{ \overline{OD} } { \overline{OP} } = \frac{ \overline{OP} } { \overline{OB} } $$. Since OB is the secant: $$ \frac{ \overline{OD} } { \overline{OP} } = \frac{ \overline{OP} } { \sec \alpha } $$ The segment OD is the cosine: $$ \frac{ \cos \alpha } { \overline{OP} } = \frac{ \overline{OP} } { \sec \alpha } $$. The segment OP is the unit radius of the circle, thus OP = 1: $$ \frac{ \cos \alpha } { 1 } = \frac{ 1 } { \sec \alpha } $$. Isolating the secant yields the formula: $$ \frac{ \sec \alpha } { 1 } = \frac{ 1 } { \cos \alpha } $$
Other Secant Formulas
The secant of an angle α can also be determined using the tangent of α: $$ \sec \alpha = \sqrt{1+ \tan^2 \alpha } $$ or $$ \sec^2 \alpha = 1+ \tan^2 \alpha $$
Proof
The radius, secant, and tangent form a right triangle where the secant serves as the hypotenuse.
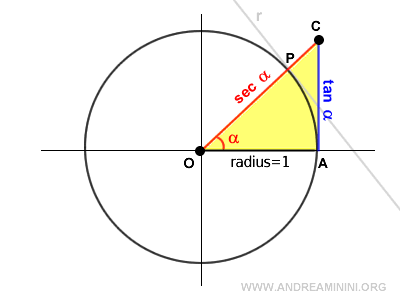
Thus, we can express the secant using the Pythagorean theorem in terms of the tangent:
$$ \sec \alpha = \sqrt{1^2+ \tan^2 \alpha } $$
$$ \sec \alpha = \sqrt{1+ \tan^2 \alpha } $$
Squaring both sides of the equation gives:
$$ ( \sec \alpha )^2 = ( \sqrt{1+ \tan^2 \alpha } )^2 $$
$$ \sec^2 \alpha = 1+ \tan^2 \alpha $$
The Graph of the Secant
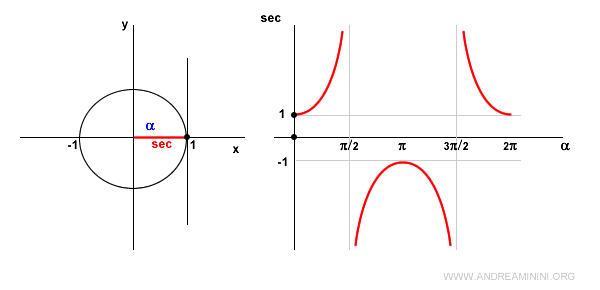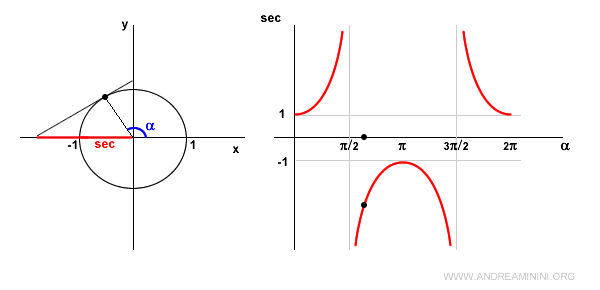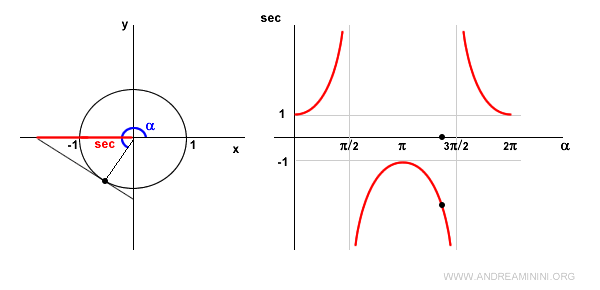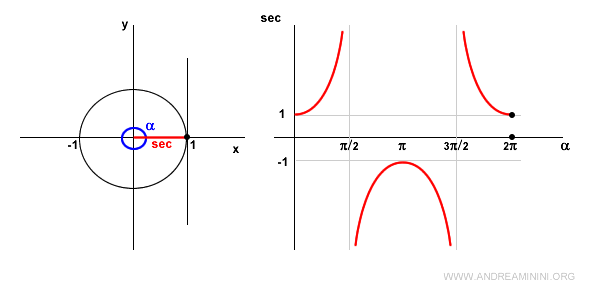
When the angle is zero (α = 0), the secant equals 1, as cos 0 = 1.
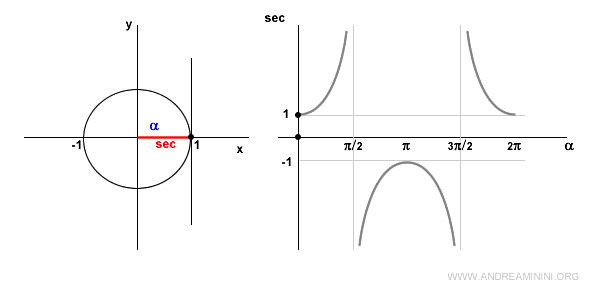
In the first quadrant, the cosine is positive, so the secant is also positive and increasing.
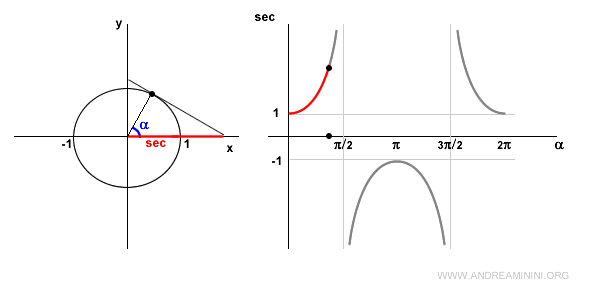
At α = π/2 (90°), the secant is undefined because cos π/2 = 0, making sec π/2 = 1/0 undefined.
In this situation, the tangent line at the point is parallel to the x-axis, resulting in no point of intersection between the two lines.
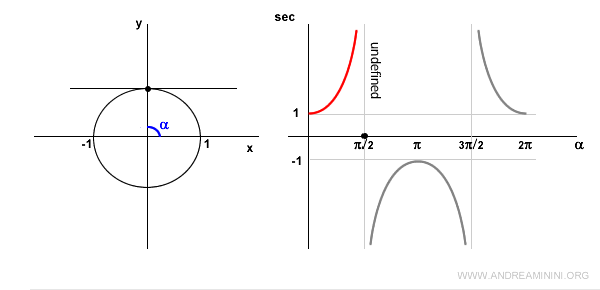
In the second quadrant, the cosine is negative, so the secant is also negative and increasing.
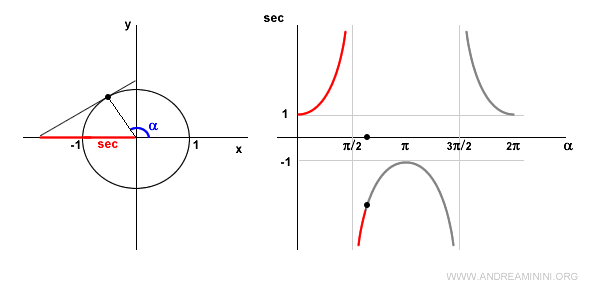
At α = π (180°), the cosine is -1, so the secant is also -1.
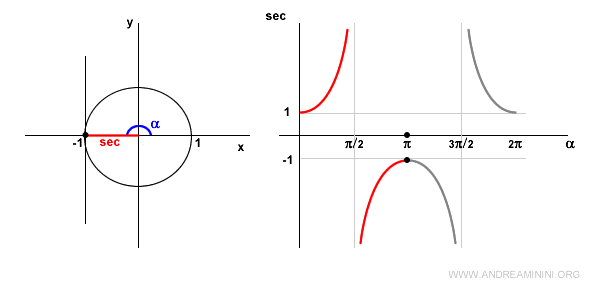
In the third quadrant, the cosine remains negative, making the secant negative but decreasing.
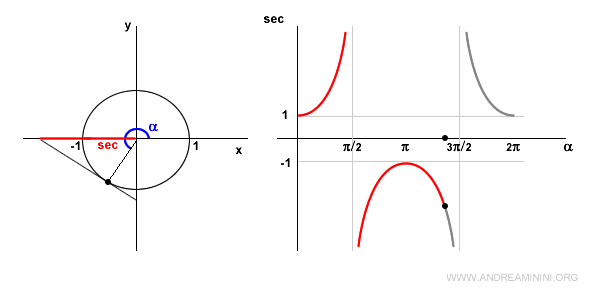
At α = 3π/2 (270°), the cosine is zero, thus the secant is undefined since 1/0 is undefined.
Similarly, the tangent line here is parallel to the x-axis, leading to no intersection points.
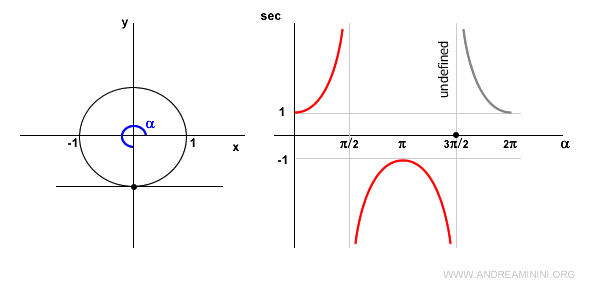
In the fourth quadrant, the cosine is positive, so the secant is also positive and decreasing.
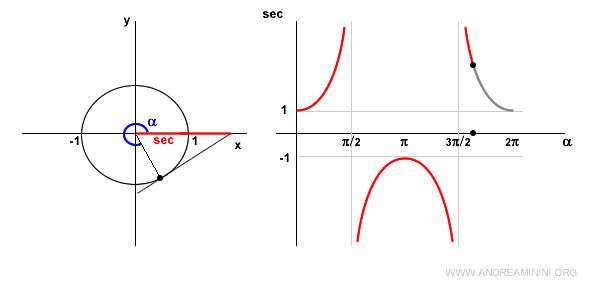
At α = 2π, the scenario returns to that of a zero-width angle (α = 0), and the secant is 1.
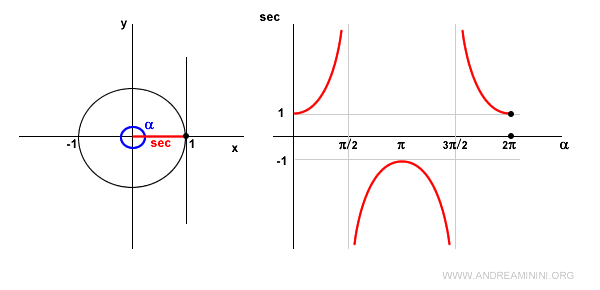
Since it is a periodic function, the pattern repeats from this point onward.
And so on.
