Hyperbolic Cosine
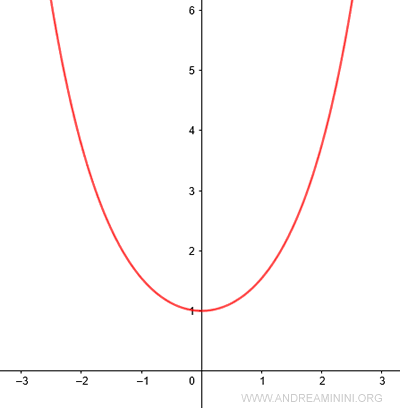
The hyperbolic cosine (cosh) is one of the hyperbolic functions in trigonometry. $$ \cosh(x) $$ Its domain is all real numbers (-∞, ∞), and its range is [1, ∞)
Unlike the cosine, the hyperbolic cosine is not calculated using the unit circle, but instead on the hyperbola x2 - y2 = 1.
Explanation
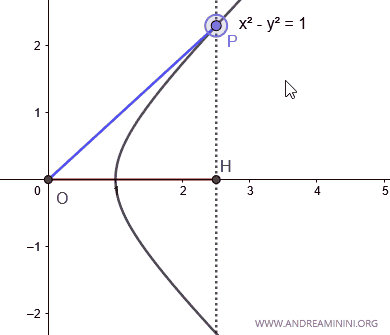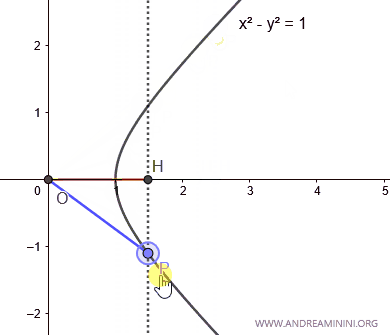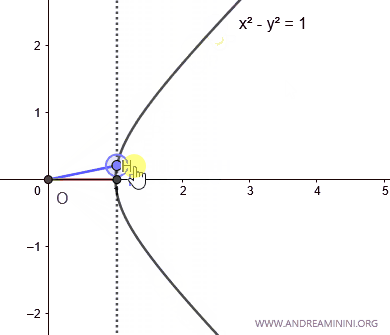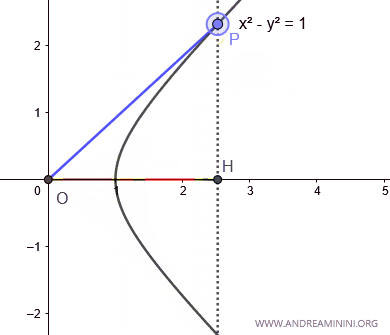
Let’s draw the graph of the hyperbola x2 - y2 = 1 on a Cartesian plane.
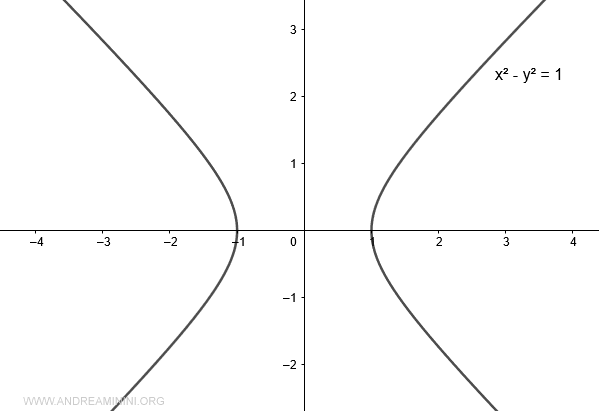
We'll focus only on the sections of the hyperbola in the first and fourth quadrants.
Take a point P on the hyperbola.
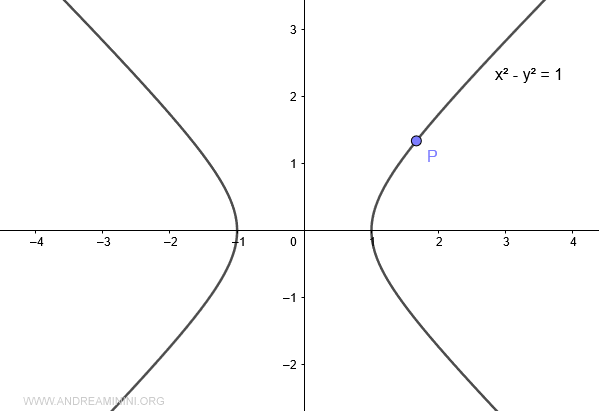
Now, draw a line connecting point P to the origin O of the graph.
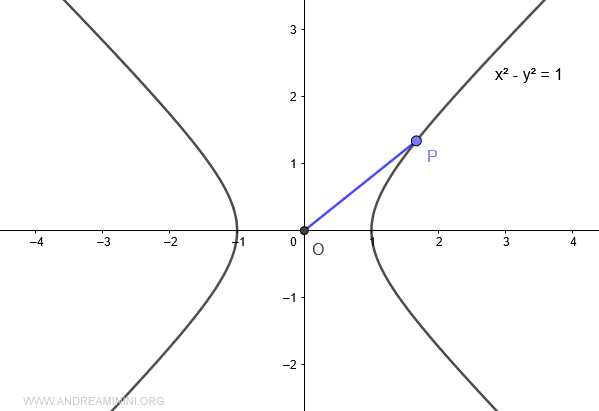
The line OP forms an angular opening between (-π/4, π/4), or (-45° to 45°).
The area A enclosed by the x-axis, the hyperbola, and line OP is the argument (x) of the hyperbolic cosine cosh(x). This area is called the hyperbolic sector.
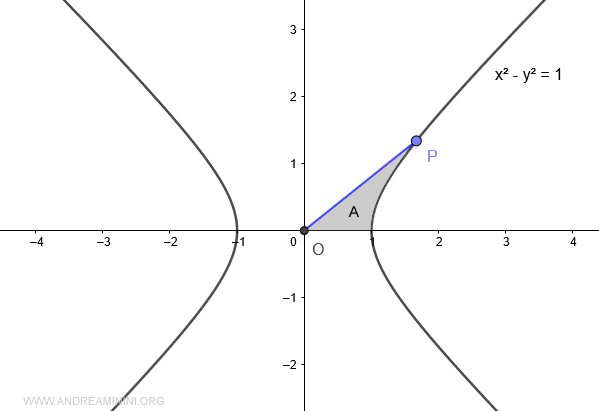
Note: Unlike in trigonometric functions (sine, cosine, tangent, etc.), in hyperbolic functions, the argument is not an angle.
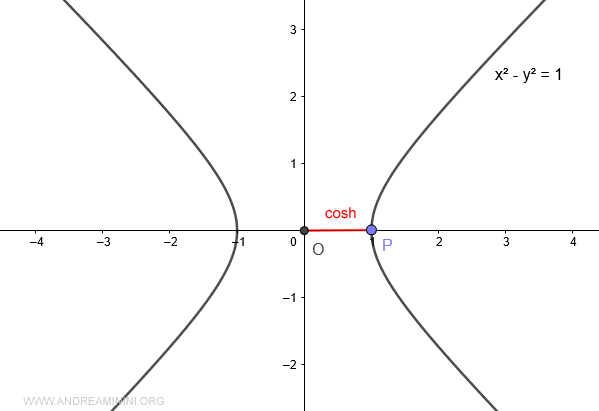
The value of the hyperbolic cosine cosh(x) is the projection of point P onto the x-axis.
Therefore, when the area A=0, the value of the hyperbolic cosine is 1.
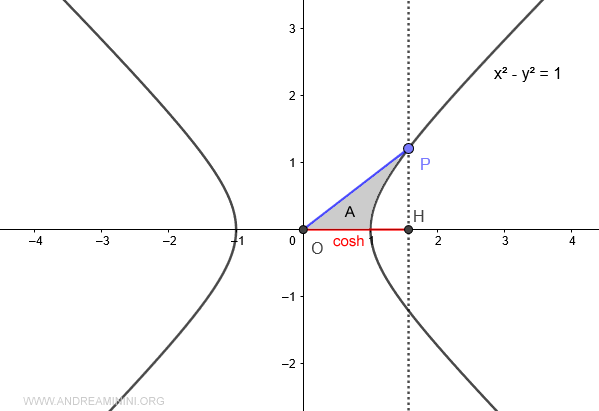
When the area A>0 (greater than zero), the hyperbolic cosine is positive.
When the area A<0 (less than zero), the hyperbolic cosine is negative.
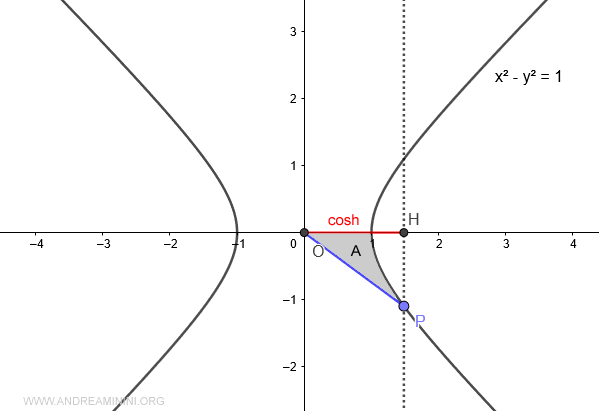
Note: The area of the hyperbolic sector is negative when point P has a negative y-coordinate, and positive when P has a positive y-coordinate.
The area of the hyperbolic sector grows indefinitely as the x-coordinate of point P increases toward infinity.
As a result, the area of the hyperbolic sector is unbounded and is a real number within the range (-∞, ∞).
However, the value of the hyperbolic cosine is always positive and is a real number in the range [1, ∞).
And so on.
