First Fundamental Identity of Trigonometry

The first fundamental identity of trigonometry states that the sum of the square of the sine and the square of the cosine is always equal to 1: $$ \sin^2 \alpha + \cos^2 \alpha = 1 $$

This identity is incredibly useful because it allows us to calculate the sine if the cosine is known, and vice versa.

$$ \sin \alpha = \pm \sqrt{1 - \cos^2 \alpha } $$

$$ \cos \alpha = \pm \sqrt{1 - \sin^2 \alpha } $$

Proof of the Identity

The proof of the first fundamental identity of trigonometry follows directly from the Pythagorean Theorem.

On the unit circle, the sine, cosine, and radius form a right triangle.

 

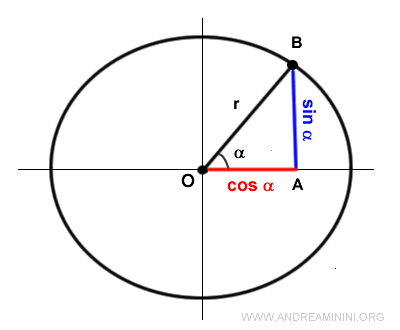
In this triangle, the sine and cosine represent the lengths of the two legs, while the radius is the hypotenuse.

According to the Pythagorean Theorem, the length of the hypotenuse is the square root of the sum of the squares of the legs:

$$ r = \sqrt{ \cos^2 \alpha + \sin^2 \alpha } $$

Squaring both sides of this equation gives:

$$ r^2 = (\sqrt{ \cos^2 \alpha + \sin^2 \alpha })^2 $$

$$ r^2 = \cos^2 \alpha + \sin^2 \alpha $$

Since the radius of the unit circle is 1 (r = 1):

$$ 1^2 = \cos^2 \alpha + \sin^2 \alpha $$

And because the square of 1 is simply 1:

$$ 1 = \cos^2 \alpha + \sin^2 \alpha $$

This confirms the first fundamental identity of trigonometry.

$$ \cos^2 \alpha + \sin^2 \alpha = 1 $$

From here, we can also derive the formulas for sine and cosine.

To isolate sine:

$$ \sin^2 \alpha = 1 - \cos^2 \alpha $$

Taking the square root of both sides:

$$ \sqrt{ \sin^2 \alpha } = \sqrt{ 1 - \cos^2 \alpha } $$

Then simplifying:

$$ \sin \alpha = \sqrt{ 1 - \cos^2 \alpha } $$

This gives us the formula for sine in terms of cosine.

Note: Similarly, we can find the formula for cosine using the fundamental identity: $$ \cos^2 \alpha + \sin^2 \alpha = 1 $$ Solving for cosine: $$ \cos^2 \alpha = 1 - \sin^2 \alpha $$ Taking the square root of both sides: $$ \sqrt{ \cos^2 \alpha } = \sqrt{ 1 - \sin^2 \alpha } $$ Then simplifying: $$ \cos \alpha = \sqrt{ 1 - \sin^2 \alpha } $$

This completes the proof.

And so on.