Triangle
A triangle is a three-sided polygon defined by its three angles.
Overview
As one of the basic shapes in Euclidean geometry, the triangle consists of a set of points bounded by a closed polyline.
The triangle's corners, known as vertices, are defined by three distinct points (A, B, C) that are not in a straight line.
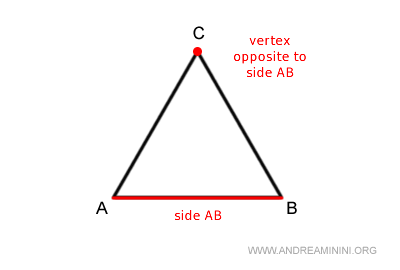
A vertex is referred to as the vertex opposite to a side when it is not part of that side.
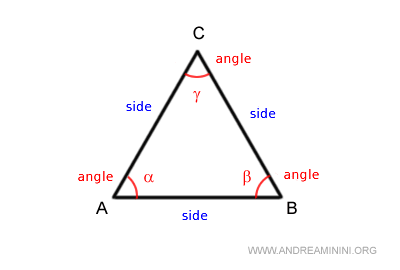
Each pair of sides in a triangle defines an internal angle, which is formed at a vertex of the triangle and flanked by the two sides.
An angle is adjacent to a side if its vertex matches one of the side's endpoints, and one of its arms extends along the side itself.
For instance, angle β is adjacent to sides AB and BC alike.
Thus, two angles are adjacent to each side of the triangle.
Angles α and β, for example, flank side AB.
An angle is termed an opposite angle to a side if it does not adjoin the side.
For example, angle γ stands opposite side AB.
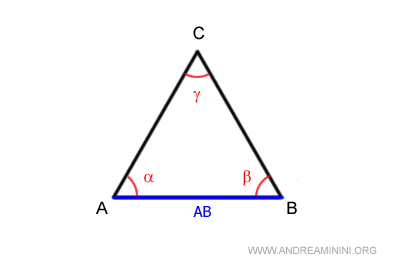
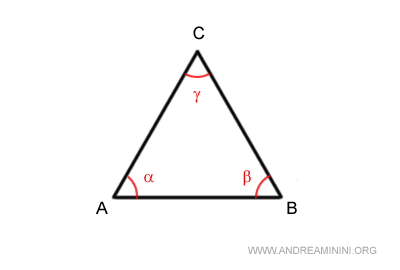
No matter the triangle's shape, the sum of its internal angles always equals 180°.
$$ \alpha + \beta + \gamma = 180° $$
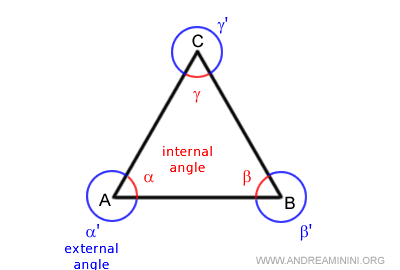
Corresponding external angles are associated with each internal angle of the triangle.
Derived from the Greek words for "three" and "angle," the triangle is a versatile shape used across various fields, such as physics and mathematics. It plays a crucial role in trigonometry, which studies the relationships between a triangle's sides and angles.
Triangle Types
Triangles are versatile shapes that can be classified in multiple ways, each revealing unique properties and characteristics.
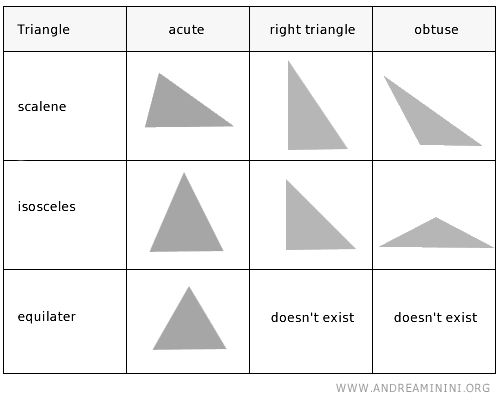
By Sides:
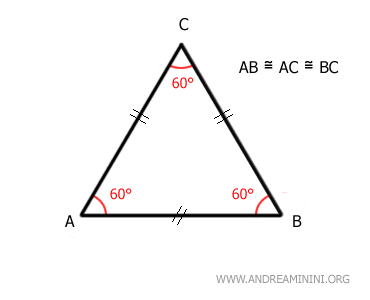
- Equilateral Triangle
An equilateral triangle features three sides of identical length, resulting in all three internal angles being equal to 60 degrees.
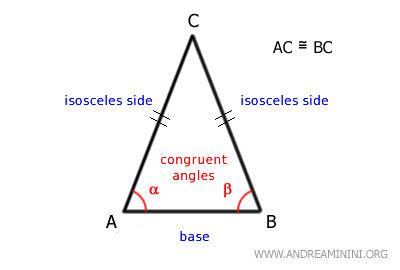
- Isosceles Triangle
Characterized by two sides of the same length, an isosceles triangle also boasts two equal angles adjacent to its base.
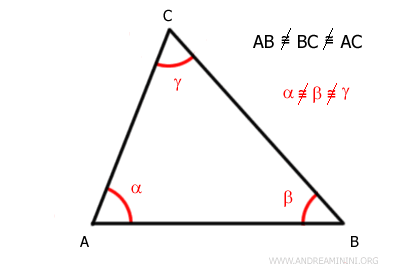
- Scalene Triangle
With three unequal sides, each angle in a scalene triangle is also distinct, adding to its asymmetrical beauty.
By Angles:
- Acute Triangle
An acute triangle has all its angles less than 90 degrees, showcasing a sharp, slender appearance.
- Obtuse Triangle
Featuring a single angle greater than 90 degrees, the obtuse triangle offers a broad, expansive feel.
- Right Triangle
The classic right triangle is easily recognized by its singular 90-degree angle, forming the basis for trigonometry.
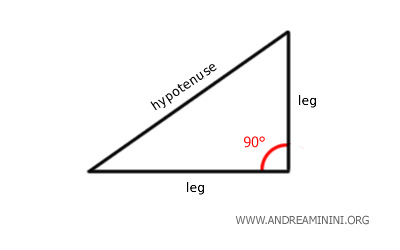
Unique to the right triangle, the sides that form the 90° angle are referred to as "legs", with the side opposite the right angle known as the "hypotenuse".
Triangle Formulas
Key formulas to measure various aspects of a triangle include:
- Area
To find a triangle's area (A), multiply the base (b) by the height (h) and divide by two: $$ A = \frac{\text{b} \cdot \text{h}}{2} $$.Alternatively, if I only know the lengths of the sides, I can use Heron's formula. $$ A = \sqrt{p(p-l_1)(p-l_2)(p-l_2)} $$ Where \( l_1 \), \( l_2 \), and \( l_3 \) are the sides and \(p = \frac{l_1+l_2+l_3}{2}\) is the semiperimeter of the triangle.
- Perimeter
The perimeter (P) is the total length around the triangle, calculated by adding the lengths of its three sides: $$ P = a + b + c $$, where a, b, and c are the side lengths.
Isosceles and equilateral triangles have their own unique formulas for calculating area and perimeter.
Triangle Centers
Triangles are known for having several important centers, including the centroid, circumcenter, and incenter, among others.
- Orthocenter
The point where a triangle's three altitudes intersect is called the orthocenter.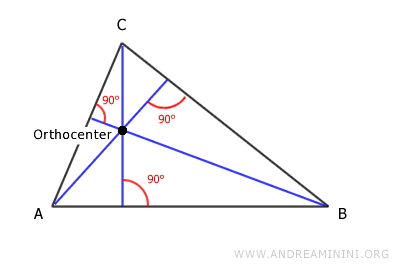
Note: Triangles have three altitudes. Depending on the triangle type, the orthocenter can be inside the triangle, outside, or at one of the vertices. It lies outside in an obtuse scalene triangle, inside in an acute scalene triangle, and at the right angle vertex in a right scalene triangle.
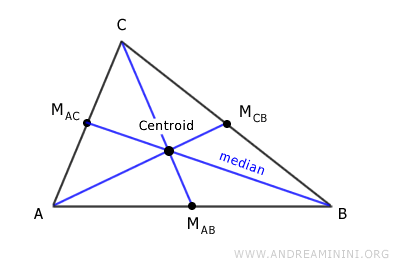
- Centroid
The centroid is the point where a triangle's three medians intersect, located inside the triangle.
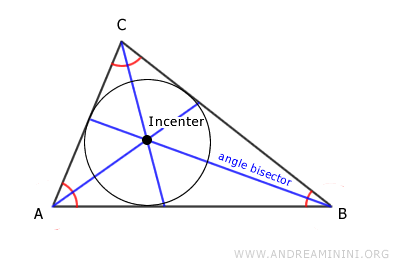
- Incenter
The incenter is the intersection point of the triangle's three angle bisectors and is the center of the inscribed circle.
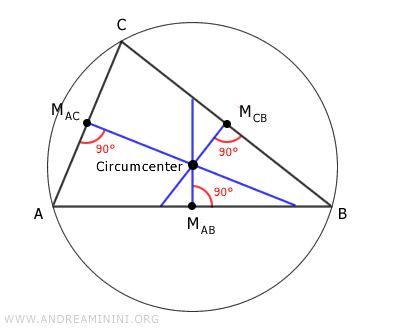
- Circumcenter
The circumcenter, where the triangle's three perpendicular bisectors meet, is the center of the circumscribed circle.
The orthocenter, centroid, circumcenter, and incenter of a triangle are all concyclic, residing on the Euler circle.
Triangle Properties
Let's delve into some properties of triangles in geometry.
- All triangles have interior angles adding up to 180°
This means the angles inside any triangle always total a straight angle. This fundamental rule applies across all triangle types. $$ \alpha + \beta + \gamma = 180° $$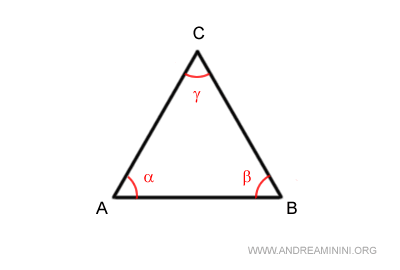
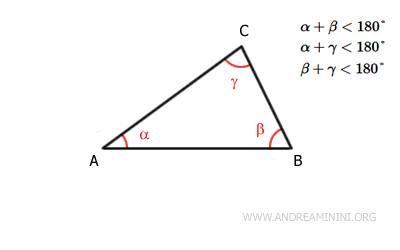
- The sum of any two internal angles is less than 180°
Specifically, in any triangle, combining any two internal angles will always give you a sum less than a straight angle (180°).
- A triangle always has at least two acute angles
A triangle must always have at least two acute angles because it can never have more than one right or obtuse angle. If it did, the sum of those two angles alone would be at least 180° - a contradiction, since the total sum of a triangle’s interior angles is always exactly 180°. This follows from the theorem stating that the sum of any two interior angles must be less than 180°.Proof. The reason a triangle must always have at least two acute angles comes directly from the interior angle sum property. If a triangle has a right angle (90°), the remaining two angles must add up to 90° (\(180° - 90° = 90°\)), which means each must be less than 90° - making them acute. Likewise, if a triangle has an obtuse angle (greater than 90°), the sum of the other two angles must be less than 90° (\(180° -\) [obtuse angle] < 90°), meaning both must also be acute. In short, a triangle can never have more than one non-acute angle without violating the fundamental angle sum rule. As a result, at least two of its angles must always be acute.
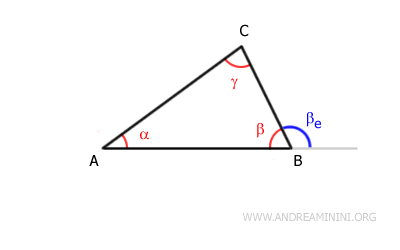
- Exterior Angle Theorem
Any exterior angle of a triangle (βe) surpasses each of its non-adjacent interior angles (α and γ), showcasing the unique relationship between a triangle's angles.
- Pythagorean Theorem
A cornerstone of geometry, this theorem reveals that in a right-angled triangle, the hypotenuse's square (the side opposite the right angle) equals the sum of the squares on the other two sides. - A circle can always be inscribed in a triangle
If you draw a triangle ABC and bisect its angles, the bisectors will always converge at a single point called the "incenter", which is equidistant from all sides of the triangle. This incenter serves as the center of a circle that can be inscribed within the triangle.

- A triangle can always be circumscribed by a circle
If you draw a triangle ABC and construct the perpendicular bisectors of its sides, these lines will always intersect at a single point known as the "circumcenter", which is equidistant from the vertices of the triangle. The circumcenter is, therefore, the center of a circle that can be circumscribed around the triangle.

Note: In the special case of an equilateral triangle, there is a specific relationship between the radius of the inscribed circle (r) and the radius of the circumscribed circle (R): $$ r = \frac{1}{3} \cdot R $$ This formula holds because, in an equilateral triangle, the ratio between the two radii remains constant. In this type of triangle, the centroid, orthocenter, circumcenter, and incenter all coincide at the same point (O).
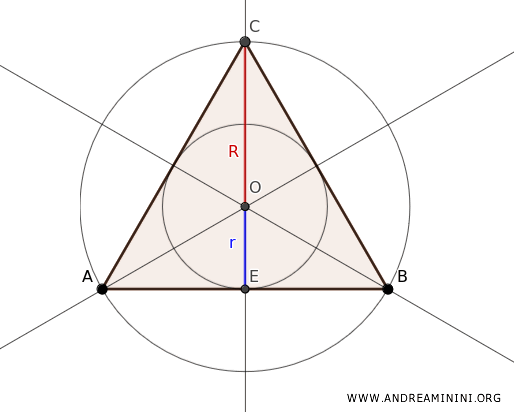
Thus, while the circumcenter and incenter both lie at the center of the triangle, the radii of the two circles differ. Since the centroid divides each median (e.g., EC) into two parts, where one is twice the length of the other, we can deduce that $ R = 2r $. Therefore, the height of the triangle ABC can be written as $ h = r + R $, and since $ R = 2r $, we find that $ r = \frac{1}{3}R $. - Every triangle features a singular centroid, the point of convergence for its medians (the segments connecting each vertex with the midpoint of the opposing side), serving as the triangle's balance point.
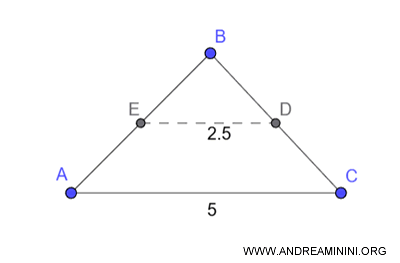
- The segment joining the midpoints of two sides of a triangle is parallel to and half the length of the third side
The segment $ED$, which joins the midpoints of two sides of a triangle ($AB$ and $BC$), is parallel to the third side $AC$ and measures exactly half its length.
- Isosceles Triangle Theorem
If a triangle has two congruent sides, then the angles opposite those sides are also congruent.Example. An isosceles triangle is defined by the congruence of its two non-base sides and the equality of its base angles. Since each base angle lies opposite one of the congruent sides, it follows that in any triangle, angles opposite equal sides must also be equal.
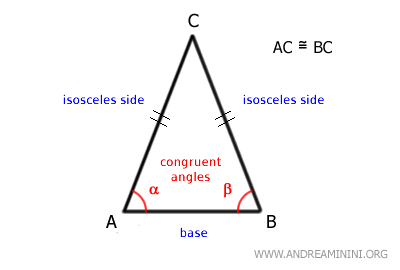
In an isosceles triangle, the base angles are always congruent due to the triangle’s inherent symmetry. The altitude from the apex to the base acts as the axis of symmetry, bisecting the triangle into two mirror-image right triangles.
And that's just the tip of the iceberg when it comes to triangle properties.
