A Triangle Always Has at Least Two Acute Angles
Every triangle must have at least two acute angles. In other words, a triangle can never contain more than one right angle or more than one obtuse angle.
This fundamental property follows directly from the rule that the sum of a triangle’s interior angles is always 180°.
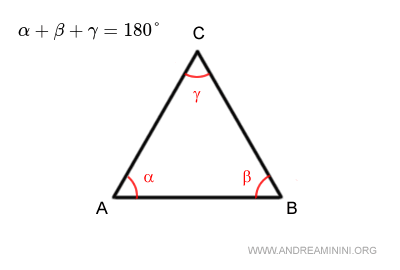
To see why this is true, let's examine the three main types of triangles:
- Acute Triangle
By definition, an acute triangle has all three angles measuring less than 90°, meaning every angle is acute.
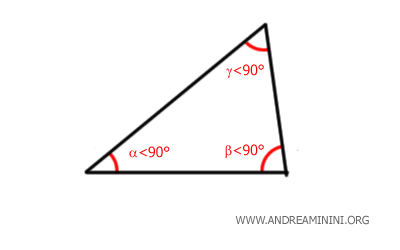
- Right Triangle
A right triangle has one angle exactly equal to 90° (a right angle). Since the total sum of a triangle’s interior angles must always be 180°, the other two angles must together add up to 90° (i.e., \(180° - 90° = 90°\)). For this to be possible, both of these angles must be less than 90°, meaning they are acute. Therefore, a triangle can never have more than one right angle.
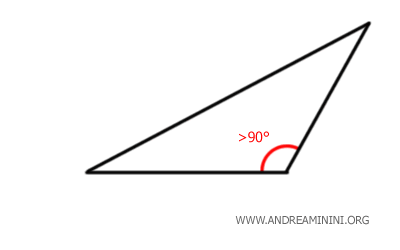
- Obtuse Triangle
An obtuse triangle contains one angle greater than 90° (an obtuse angle). Since the total sum of a triangle’s angles is fixed at 180°, the remaining two angles must together sum to a value less than 90° (because \(180°\) minus an obtuse angle will always be less than 90°). This means both of these remaining angles must be acute. As a result, a triangle can never have more than one obtuse angle.
In conclusion, since a triangle cannot have two right angles or two obtuse angles, at least two of its angles must always be acute, regardless of the type of triangle.
And that’s why this rule holds true.
