Sum of Two Interior Angles of a Triangle
The sum of any two interior angles of a triangle is always less than 180°.
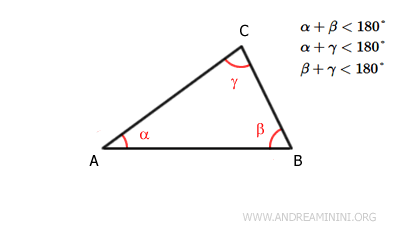
For example, in any given triangle ABC:
The following inequalities hold true:
$$ \alpha + \beta < 180° \\ \alpha + \gamma < 180° \\ \beta + \gamma < 180° $$
An important corollary follows from this theorem:
A triangle always has at least two acute angles (less than 90°).
In other words, a triangle cannot have more than one right angle or one obtuse angle.
If it did, the sum of two interior angles would be equal to or greater than 180° (a straight angle).
Proof
Consider any triangle ABC:
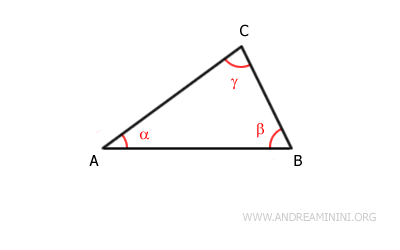
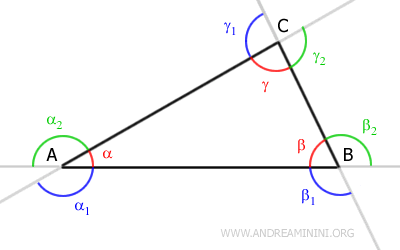
The triangle has three interior angles (α, β, γ), and each interior angle has two adjacent exterior angles:
For example, the interior angle β has two adjacent exterior angles βe and βe'
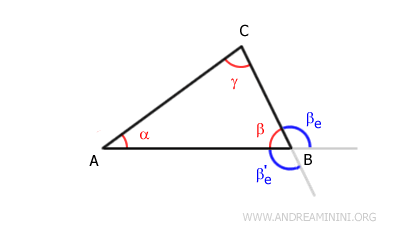
Consider the exterior angle βe:
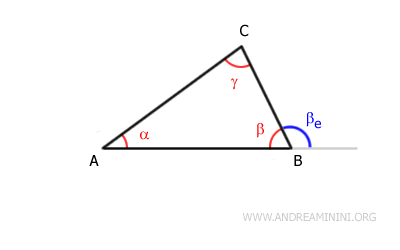
According to the exterior angle theorem, an exterior angle is greater than either of the non-adjacent interior angles.
Therefore, for the exterior angle β, we have the following inequalities:
$$ β_e > α $$
$$ β_e > γ $$
In other words, the exterior angle βe is greater than either of the non-adjacent interior angles (α and γ).
The interior angle β is not considered because it is adjacent to βe.
Now, consider the first inequality:
$$ β_e > α $$
By the invariant property of inequalities, we add the angle β to both sides:
$$ β_e + β > α + β $$
Knowing that the sum of an interior angle and its adjacent exterior angle is a straight angle (180°), we deduce that βe + β = 180°.
$$ 180° > α + β $$
Therefore, the sum of the two interior angles α and β is always less than 180°.
$$ \alpha + β < 180° $$
Repeating the proof with the other exterior angles of the triangle yields the same result.
And so on.
