Equilateral Triangle

A triangle is called an equilateral triangle if all three sides are of equal length.

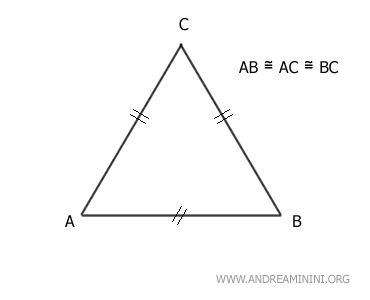
In other words, an equilateral triangle has three sides of the same length.

The term "equilateral" comes from Latin and means "equal sides."

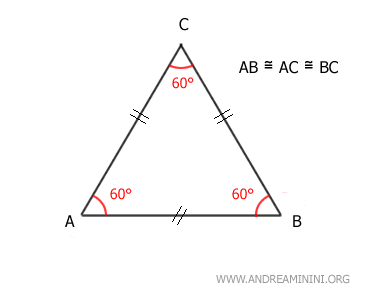
Another key feature of equilateral triangles is that they also have all angles equal, with each angle measuring 60°. In any triangle, the sum of the angles is 180°, which is 60° + 60° + 60°.

Formulas

The main formulas for calculating the properties of an equilateral triangle:

• Perimeter
  Multiply the length of one side by three. $$ P = 3 l $$
• Area
  Like any triangle, the area can be found by multiplying the base (b) by the height (h) and dividing by two. $$ A = \frac{b \cdot h}{2} $$ For equilateral triangles, you can also use this formula: $$ A = \frac{l^2 \cdot \sqrt{3}}{4} $$
• Side Length
  You can find the length of a side if you know the height (h) of the equilateral triangle using this formula (proof): $$ l = \frac{2h}{\sqrt{3}} $$ Alternatively, the side length of an equilateral triangle is equal to the radius (r) of the circumscribed circle multiplied by the square root of three (see proof): $$ l = r \cdot \sqrt{3} $$ You can also determine the side length from the radius of the inscribed circle (proof): $$ l = 2r \sqrt{3} $$
• Height
  The formula for the height is derived from the side length formula (proof): $$ h = \frac{l}{2} \sqrt{3} $$

Note: The fact that all sides of an equilateral triangle are equal allows for calculating the area and perimeter using alternative formulas by applying the Pythagorean theorem to half of the equilateral triangle.

How to Draw an Equilateral Triangle

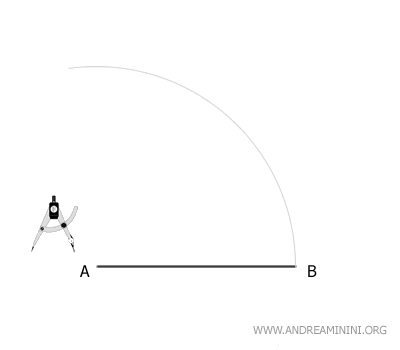
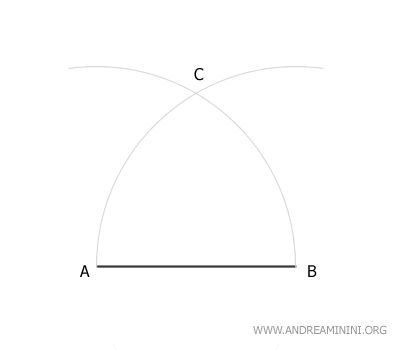
To construct an equilateral triangle, start by drawing a line segment AB.

Next, place the compass at point A and draw an arc with radius AB.

Keeping the compass at the same width (radius AB), place the compass at point B and draw a second arc.

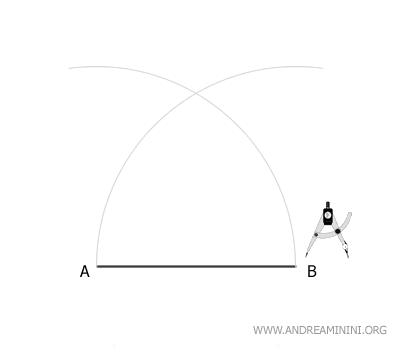
The two arcs intersect at point C.

This point is the third vertex of the equilateral triangle.

Draw two line segments, AC and BC.

The final result is an equilateral triangle.

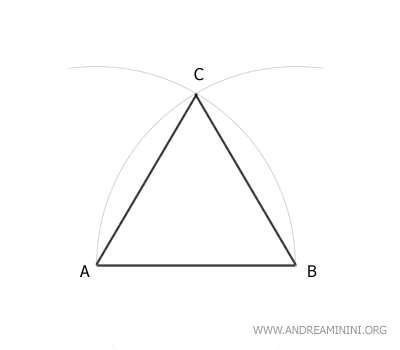
All sides of the triangle are equal, meaning they have the same length.

To learn more techniques for constructing an equilateral triangle, click here.

Insights into Equilateral Triangles

Equilateral triangles have the following characteristics:

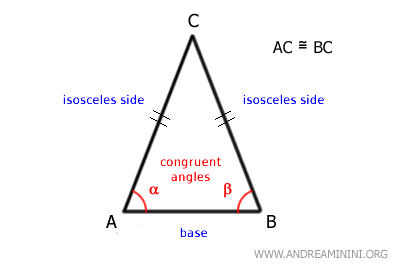
• An equilateral triangle is an isosceles triangle with three equal bases
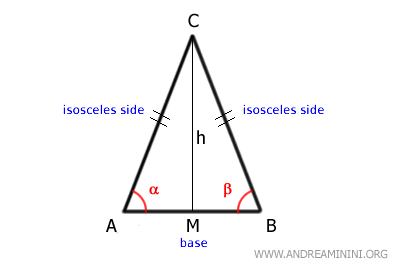
  A triangle is isosceles if it has two congruent sides (AC≅BC). The remaining side (AB) is the base and has two congruent angles (α≅β).
  
  In an equilateral triangle, all three sides are congruent (AC≅BC≅AB). Therefore, any side can serve as the base, with the other two sides forming an isosceles triangle.
  
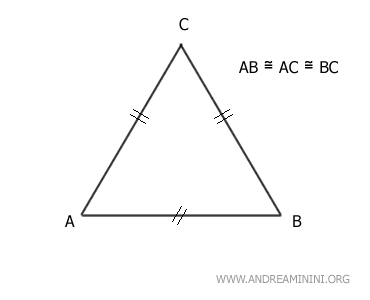
  Thus, equilateral triangles are a subset of isosceles triangles where the base is congruent to the other sides.

  This is crucial because it allows us to use the same theorems for both equilateral and isosceles triangles to prove various properties.

• All angles in an equilateral triangle are congruent
  In an equilateral triangle, all three angles are equal.
  

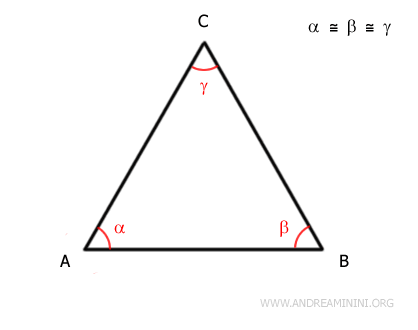
  Proof. An equilateral triangle can be viewed as an isosceles triangle with three bases. In an isosceles triangle, the angles at the base are congruent (isosceles triangle theorem).
  
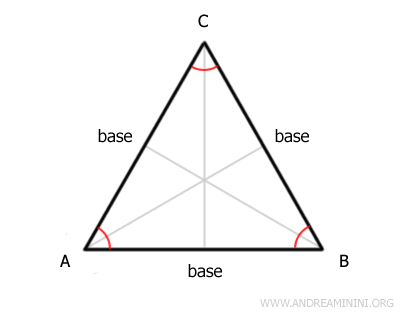
  In an equilateral triangle, there are three bases.
  
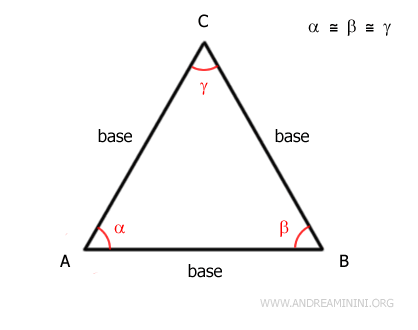
  Knowing that the base angles are congruent, we have $$ \alpha = \beta $$ $$ \beta = \gamma $$ $$ \alpha = \gamma $$ By the transitive property, we conclude that $$ \alpha = \beta = \gamma $$ Therefore, all angles in an equilateral triangle are congruent.

• The angles of an equilateral triangle measure 60°
  In an equilateral triangle, each angle measures 60 degrees.
  

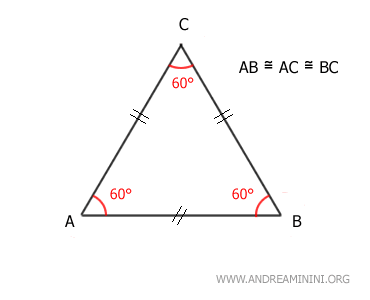
  Proof. The sum of the angles in a triangle is always 180°. Since all three angles in an equilateral triangle are congruent, we simply divide 180° by three: $$ 180° \ : \ 3 = 60° $$

• In an equilateral triangle, each angle bisector is also a median and an altitude
  The heights, medians, angle bisectors, and the perpendicular bisectors drawn from any vertex to the center of the opposite side all coincide in the same segment, known as the axis of the triangle.
  
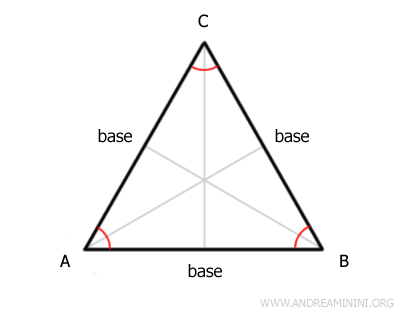
  Therefore, in an equilateral triangle, the centroid coincides with the incenter, the circumcenter, and the orthocenter.

  Proof. An equilateral triangle is an isosceles triangle with three equal bases. Therefore, the same theorems that apply to isosceles triangles also apply to equilateral triangles. Specifically, recall that in an isosceles triangle, the angle bisector is also the altitude and median to the base.
  
  In an equilateral triangle, there are three bases, so all angle bisectors are also altitudes and medians to their respective bases.
  

• Each angle of an equilateral triangle is one-third of a straight angle

  Proof. According to the theorem on the sum of the interior angles, the sum of the interior angles of a triangle equals a straight angle (180°) $$ \alpha + \beta + \gamma = 180° $$ Knowing that the interior angles of an equilateral triangle are congruent, each angle is one-third of a straight angle (180°). $$ \alpha = \beta = \gamma = \frac{180°}{3} = 60° $$

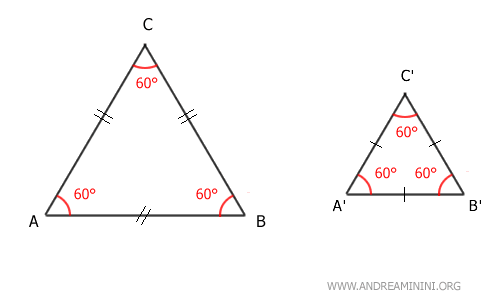
• Any two equilateral triangles are similar
  Two equilateral triangles, even of different sizes, always have congruent corresponding angles. Therefore, according to the first principle of triangle similarity, two equilateral triangles are similar.
  
• For an equilateral triangle, the Euler line cannot be drawn because the centroid, circumcenter, and orthocenter all coincide at a single point, so they are not collinear. Instead, there are infinitely many lines passing through this point.
• The area of an equilateral triangle can be calculated using the formula:
  $$ A = \frac{l^2 \cdot \sqrt{3}}{4} $$ where l is the length of a side.
• The side of an equilateral triangle is equal to the radius of the circumscribed circle times √3 $$ l = r \cdot \sqrt{3} $$

  The radius of the circumscribed circle that touches all three vertices of the triangle is equal to (l/√3), where l is the length of a side of the triangle. $$ r = \frac{l}{\sqrt{3}} $$
  
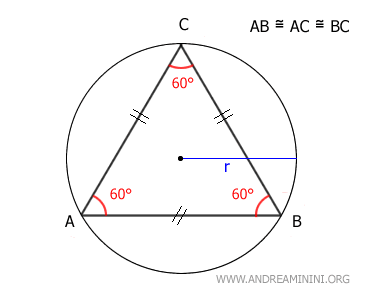
  Therefore, the side of the equilateral triangle is equal to the radius of the circumscribed circle times √3: $$ l = r \cdot \sqrt{3} $$

• The radius of the inscribed circle that touches all three sides of the triangle is equal to (l/2√3), where l is the length of a side of the triangle. $$ r = \frac{l}{2 \cdot \sqrt{3}} $$ Consequently, the side of the equilateral triangle can also be obtained from the radius of the inscribed circle: $$ l = 2 \sqrt{3} \cdot r $$
  
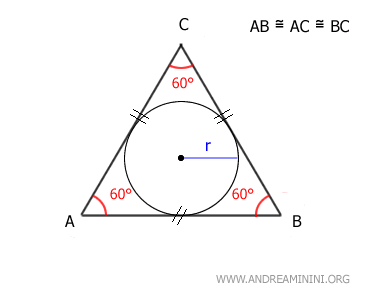
• The relationship between the inscribed and circumscribed circles
  In an equilateral triangle, there is a consistent relationship between the radius of the inscribed circle (denoted as \(r\)) and the radius of the circumscribed circle (denoted as \(R\)). This relationship is expressed by the formula: $$ r = \frac{1}{2} \cdot R $$ This is because, in an equilateral triangle, all the key points (the centroid, orthocenter, circumcenter, and incenter) coincide at a single point (O).
  
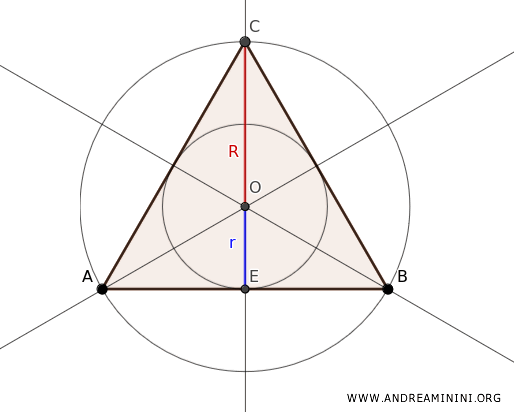
  In particular, the circumcenter and incenter overlap, meaning the inscribed and circumscribed circles share the same center but have different radii. Since the centroid divides each median (e.g., EC) into two segments, one twice the length of the other, we can conclude that the radius of the circumscribed circle \(R\) is double that of the inscribed circle \(r\), i.e., $ R = 2r $. The height of the equilateral triangle \(ABC\) can be written as the sum of the two radii: $ h = r + R $. Substituting \(R = 2r\) into this equation gives $ h = r + 2r = 3r $. Given \( h = r + R \) and \( h = 3r \), we can conclude $ 3r = r + R $. Simplifying this equation yields $2r = R $, which confirms that \(r = \frac{1}{2}R\).

These properties apply only to equilateral triangles.

And so on.