Triangle Area Calculation

The area of a triangle is determined by a simple formula. Given b as the length of the triangle's base and h as its height (the perpendicular line from the base to the opposite vertex), the area A is calculated as: $$ A = \frac{b \cdot h}{2} $$

This approach originates from understanding a triangle as half of a parallelogram sharing the same base and height.

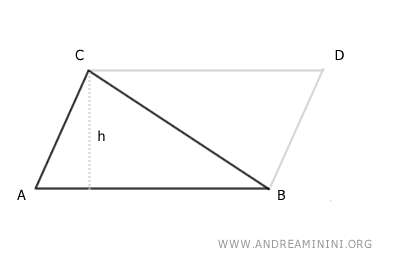
This geometric perspective is quite insightful, bridging the properties between two distinct shapes.

A parallelogram's area is found by multiplying its base by its height.

Hence, to find a triangle's area, you multiply the base by the height and divide by two.

Reverse Formulas

Aside from the standard formula, there are inverse formulas useful for finding a triangle's base or height if its area is known.

$$ b=\frac{2A}{h} $$

Similarly, you can determine the height.

$$ h=\frac{2A}{b} $$

These reverse formulas prove to be incredibly useful for tackling geometry problems.

An Example

Consider an example of a scalene triangle with a height of h=7.0588 and a base of c=17.

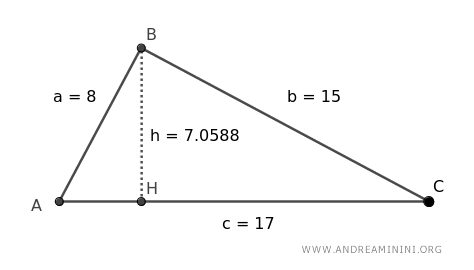
To compute the triangle's area, simply multiply the base by the height.

$$ A=\frac{c \cdot h}{2} = \frac{17 \cdot 7.0588}{2} \approx 60 $$

The calculated area of the triangle is A=60.

Area of a Right Triangle

In the special case of a right triangle, the area is calculated by multiplying the two legs together.

$$ A = \frac{c_1 \cdot c_2}{2} $$

This calculation is straightforward because one leg serves as the base (b=c₁) and the other as the height (h=c₂), with the product then halved.

Heron's Formula

Heron's formula enables the calculation of any triangle's area, given just the lengths of its sides.

$$ A = \sqrt{p \cdot (p-l_1) \cdot (p-l_2) \cdot (p-l_3)} $$ where \( l_1 \), \( l_2 \), and \( l_3 \) are the sides and \(p = \frac{l_1+l_2+l_3}{2}\) represents the semiperimeter of the triangle.

This formula is particularly valuable when a triangle's height is unknown or challenging to determine.

Example

Using the previously mentioned triangle as an example:

Let's calculate the area using Heron's formula based solely on the lengths of the sides: a=8, b=15, c=17.

First, find the semiperimeter of the triangle.

$$ p = \frac{8+15+17}{2} = 20 $$

Then, apply Heron's formula with the semiperimeter p=20.

$$ A = \sqrt{20 \cdot (20-8) \cdot (20-15) \cdot (20-17)} $$

$$ A = \sqrt{3600} $$

$$ A = 60 $$

This method also results in an area of 60, consistent with the earlier calculation.

Finding the Area of a Triangle Using Trigonometry

You can also calculate the area of a triangle using trigonometry.

The area of a triangle is half the product of two sides, l₁ and l₂, and the sine of the angle (α) between them. $$ Area = \frac{1}{2} \cdot (l_1 \cdot l_2) \cdot \sin \alpha $$

Here, l₁ and l₂ are two adjacent sides of the triangle, and α is the angle between them.

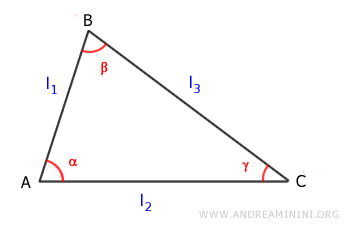
This method works for any other angle in the triangle along with its adjacent sides.

$$ Area = \frac{1}{2} \cdot (l_1 \cdot l_3) \cdot \sin \beta $$

$$ Area = \frac{1}{2} \cdot (l_2 \cdot l_3) \cdot \sin \gamma $$

This approach applies to all types of triangles (isosceles, right, scalene).

Example

Here’s an example with a scalene triangle:

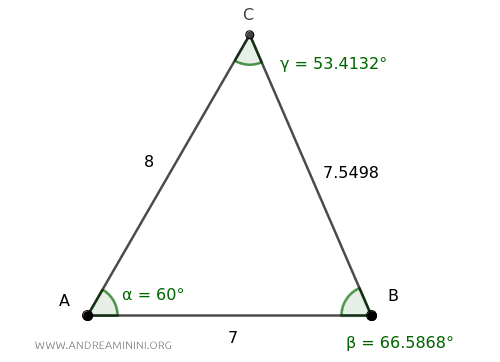
Angle α measures 60°, and the adjacent sides are AB=7 and AC=8.

To calculate the area, I’ll use the formula:

$$ Area = \frac{1}{2} \cdot (l_1 \cdot l_2) \cdot \sin \alpha $$

In this case, $ \alpha = 60° $, $ l_1 = \overline{AB}=7 $, and $ l_2 = \overline{AC}=8 $

$$ Area = \frac{1}{2} \cdot (7 \cdot 8) \cdot \sin 60° $$

$$ Area = \frac{1}{2} \cdot (56) \cdot \sin 60° $$

$$ Area = 28 \cdot \sin 60° $$

Since $ \sin 60° =  \frac{\sqrt{3}}{2} $

$$ Area = 28 \cdot \frac{\sqrt{3}}{2} $$

$$ Area = 14 \cdot \sqrt{3} $$

$$ Area = 24.2487 $$

So, the area of triangle ABC has been found using trigonometry.

Verification. To check the result, I’ll measure a height of the triangle.

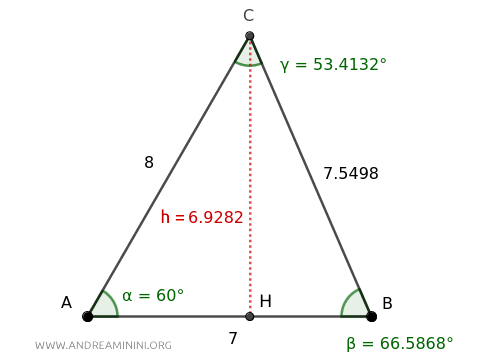
Then, I’ll calculate the area using the standard formula: base times height divided by two. $$ Area = \frac{\overline{AB} \cdot h}{2}=\frac{\overline{7} \cdot 6.9282}{2}=24.2487$$ The result is the same, confirming the calculation with the trigonometric formula.

And that’s it!