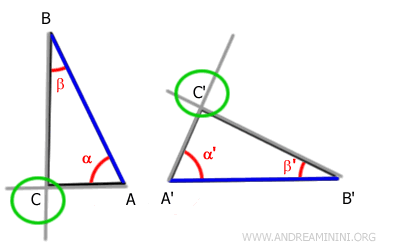
Second Criterion for Triangle Congruence
Two triangles are congruent if two corresponding angles are congruent and the side adjacent to these angles is also congruent in both triangles.
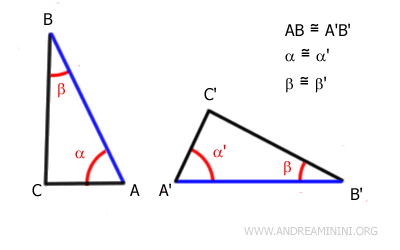
In other words, triangles are congruent when they have two angles of the same measure and the side between these two angles is the same length in both triangles.
This criterion is also known as ASA (Angle-Side-Angle).
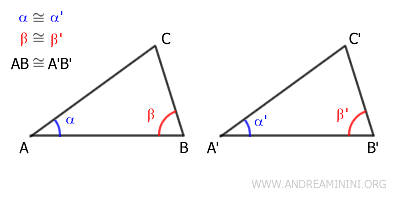
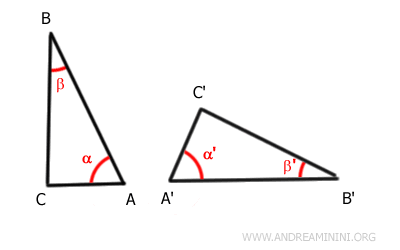
For example, consider these two triangles ABC and A'B'C'.
The angles α≅α' and β≅β' are congruent, meaning they have the same measure.
The sides adjacent to the angles AB≅A'B' are also congruent, meaning they have the same length.
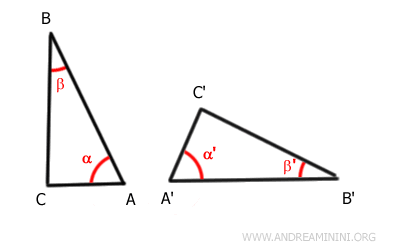
From this, we deduce that the other sides and angles are also congruent.
Therefore, the two triangles are congruent. In other words, according to the definition of congruence, they can be perfectly overlapped point by point after a rigid motion.
Proof
The second criterion for congruence is a theorem because it can be proven.
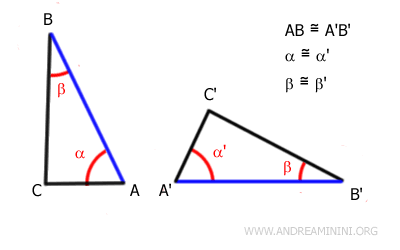
Let's take two triangles ABC and A'B'C' as an example.
By hypothesis, the angles α≅α' and β≅β' are congruent, and the side adjacent to these angles AB≅A'B' is congruent.
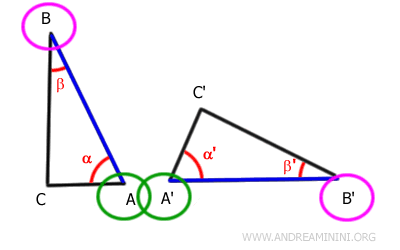
If the sides AB≅A'B' are congruent, then they are superimposable.
This means that the endpoints of the segments AB and A'B' are superimposable.
In other words, the points A and A' and the points B and B' coincide.
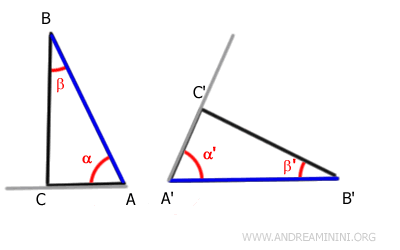
Since the angles α≅α' are also congruent, the rays containing the sides AC and A'C' are superimposable.
Similarly, since the angles β≅β' are congruent, the rays containing the sides BC and B'C' are superimposable.
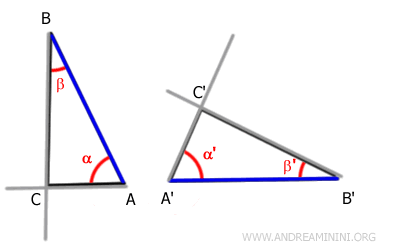
Therefore, the rays intersect at the same point.
This means that the points C and C' are superimposable.
In conclusion, all the vertices of the two triangles are superimposable in order.
This means that all the sides are congruent: AB≅A'B', BC≅B'C', AC≅A'C'.
Consequently, all the angles between the sides are also congruent.
Therefore, the two triangles are congruent.
Alternative Proof
In this case, I'll use a proof by contradiction.
Consider two triangles, ABC and A'B'C', where two angles are congruent, \( \alpha \cong \alpha' \) and \( \beta \cong \beta' \), and one side is also congruent, \( AB \cong A'B' \).
Now, let's assume - contrary to what we want to prove - that the two triangles are not congruent.
$$ ABC \not \cong A'B'C' $$
If this were true, then the side AC would have to be either longer or shorter than A'C'.
Suppose AC is longer, meaning $ AC > A'C' $. In this case, we can locate a point P along AC such that $ AP \cong A'C' $.
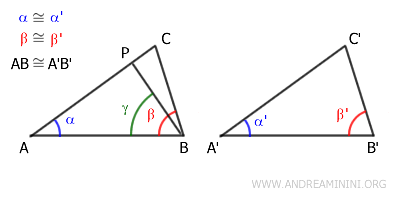
Now, consider the two triangles ABP and A'B'C'. They satisfy the following conditions:
- They share a congruent angle by assumption: \( \alpha \cong \alpha' \).
- They share a congruent side by assumption: \( AB \cong A'B' \).
- By construction, we also have \( AP \cong A'C' \).
By the first congruence theorem, these two triangles must be congruent, meaning all corresponding sides and angles are equal.
$$ ABP \cong A'B'C' $$
In particular, this implies that the corresponding angles \( \gamma \) and \( \beta' \) must be congruent.

However, our initial assumption states that \( \beta \cong \beta' \), which means, by transitivity, we must also have \( \gamma \cong \beta \).
$$ \gamma \cong \beta' \cong \beta $$
But this leads to a contradiction. Since point \( P \) lies somewhere within the segment \( AC \), the angle \( \gamma \) must be smaller than \( \beta \), which contradicts our previous conclusion.
Since our assumption - that the two triangles are not congruent - has led to a contradiction, it must be false.
Therefore, the opposite must be true: the two triangles are congruent.
Note: The same argument holds if we assume \( AC < A'C' \), meaning the sides AC and A'C' must be congruent.
Generalized ASA Triangle Congruence Criterion
The second criterion for triangle congruence also has an extended form, known as the 'generalized second criterion' or the 'fourth criterion for congruence'.
Two triangles are congruent if they have two congruent angles and one congruent side in the same sequence, even if the side is not necessarily between the two angles.
In this case, the congruent side of the triangle can be any side; it does not have to be the side between the two angles.
In other words, the congruent angles do not need to be adjacent to the congruent side of the triangles.
However, it is essential that the angles and the side correspond in the same relative order in both triangles.
Example. These two triangles have corresponding angles $ \alpha \cong \alpha' $ and $ \beta \cong \beta' $, as well as a congruent side $ BC \cong BC' $. Since the angles and the side are arranged in the same order, we can apply the generalized ASA criterion and conclude that $ ABC \cong A'B'C' $.

So far, so good. Now let’s take triangle ABC and use a compass centered at point A to draw an arc with radius AB, intersecting segment AC at point C′. Then, draw segment B′C′ parallel to BC. This gives us a new triangle, AB′C′. By construction, these two triangles also have two equal angles $ \alpha $ and $ \beta \cong \beta' $, and one congruent side $ AB \cong B'C' $. However, the triangles are not congruent, $ ABC \not \cong AB'C' $, because the angles and the side do not match in the same relative order.
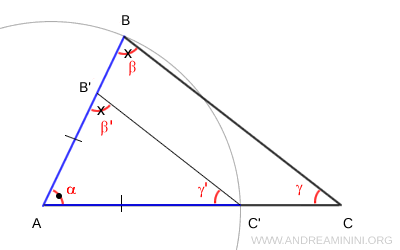
This clearly demonstrates that, in order to apply the generalized ASA congruence criterion, the angles and the side must be corresponding in order in both triangles.
Proof
According to the theorem on the sum of the interior angles of a triangle, the sum of the interior angles of a triangle is equal to a straight angle (180°).
$$ \alpha + \beta + \gamma = 180° $$
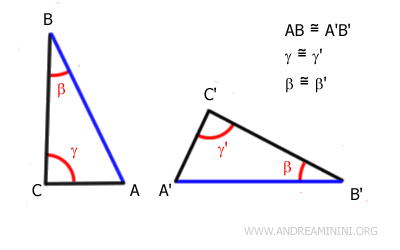
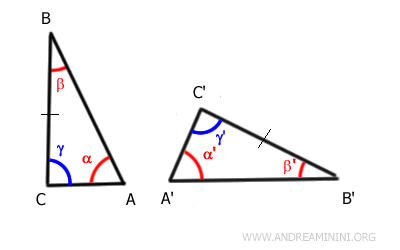
Therefore, if two angles in triangles ABC and A'B'C' are congruent, α≅α' and β≅β', then the third angle is also congruent γ≅γ' by difference
The remaining angle gamma in both triangles can be found by difference.
$$ \gamma = 180° - \alpha -\beta $$
$$ \gamma' = 180° - \alpha' -\beta' $$
Knowing that α≅α' and β≅β', we deduce that the angle γ≅γ' is also congruent
$$ \gamma \cong \gamma' $$
Now, let’s assume that triangles ABC and A′B′C′ also share a congruent side, with $ BC \cong B'C' $, and that this side appears in the same relative position in both triangles.
In this case, since the angles $ \gamma \cong \gamma' $ are also congruent, we can conclude that triangles $ ABC \cong A'B'C' $ are congruent by the ASA (Angle-Side-Angle) congruence criterion. The two triangles have a common side $ BC \cong B'C' $ and two adjacent angles $ \gamma \cong \gamma' $ and $ \beta \cong \beta' $ that are congruent and appear in the same sequence.
Therefore, triangles ABC and A'B'C' are congruent if they have one congruent side and two congruent angles, even if these angles are not adjacent to the side in question.
Alternative Proof
The second criterion for triangle congruence can be proven by contradiction.
Consider two triangles ABC and A'B'C'.

By hypothesis, the angles α≅α' and β≅β' are congruent, and the side adjacent to these angles AB≅A'B' is congruent.
Therefore, by the second criterion of congruence, the two triangles are congruent.
For contradiction, we attempt to prove that the sides not adjacent to the angles, AC and A'C', are not congruent, meaning AC≠A'C' and have different lengths.
According to the segment transport postulate, this means there is a point D on AC such that AD=A'C'.
We draw segment DB and consider triangle ADB.
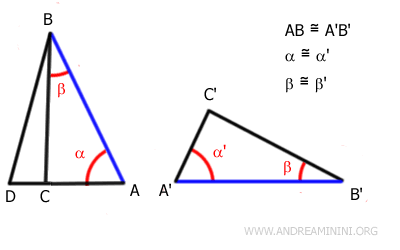
By the first criterion of congruence, the two triangles ABD and A'B'C' are congruent.
Why? If the side AD≅A'C' is congruent, from the initial hypothesis we already know that the side AB≅A'B' is also congruent, and the angle α≅α' between them is congruent. Therefore, two sides and the angle between them are congruent. By the first criterion of congruence, the two triangles ABD and A'B'C' are congruent.
If the two triangles ABD and A'B'C' are congruent, then the angle at vertices D and C' is also congruent.
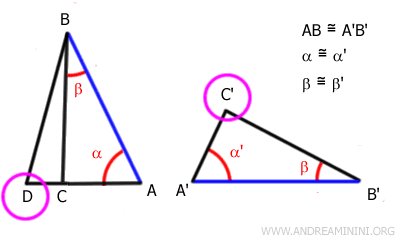
However, by the initial hypothesis, the angle at vertices C and C' is congruent because the remaining angles α≅α' and β≅β' are congruent.
According to Euclid's fifth postulate, the sum of the interior angles of a triangle is always equal to a straight angle (180°) in Euclidean geometry. $$ \alpha + \beta + \gamma = 180° $$ Therefore, if two angles are known, the measure of the third angle is also known by difference. So if two angles have the same measure, α≅α' and β≅β', then the measure of the third angle is also the same: $$ 180°-α-β≅180°-α'-β' $$
Therefore, by the transitive property, the angle at vertex D is congruent to the angle at vertex C.
Thus, the sides AD and AC must be congruent: AD≅AC.
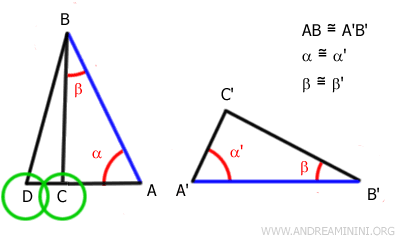
Knowing that AD≅A'C', if AD≅AC then also AC≅A'C'
$$ \overline{AC} \cong \overline{AD} \cong \overline{A'C'} $$
This means that the sides AC and A'C' cannot have different lengths. The thesis AC≠A'C' is false.
Consequently, the hypothesis contrary to the thesis AC≅A'C' is true, meaning the sides AC and A'C' are congruent.
Therefore, to establish the congruence of two triangles, it is sufficient that two angles and any side are congruent.
And so on.
