First Triangle Congruence Theorem
The first triangle congruence theorem states that two triangles are congruent if they have two sides and the included angle congruent in the same order.
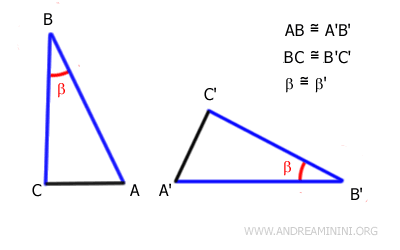
In other words, two triangles are congruent if two sides and the included angle are identical in both triangles.
This congruence theorem is also known as the SAS (Side-Angle-Side) criterion.
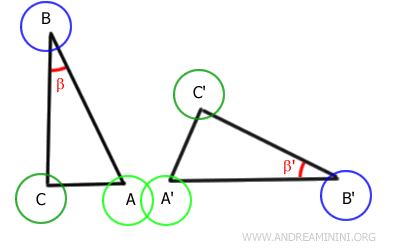
For example, consider these two triangles ABC and A'B'C'
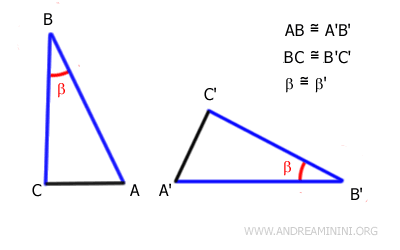
The sides AB and BC of the first triangle are respectively congruent to the sides A'B' and B'C' of the second triangle, meaning they have the same length even though their orientations are different.
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
Additionally, the angles β and β' between these pairs of sides are congruent, meaning they have the same measure.
$$ \beta \cong \beta' $$
Therefore, according to the first congruence theorem, the two triangles are congruent.
If the congruent angle is not included between the two sides, the triangles are not necessarily congruent. For example, consider triangle ABC. Then, draw a circle with radius AC and center A. The arc intersects the extension of segment AC at point D. In this way, you can draw another triangle ACD with two sides congruent to the previous triangle.
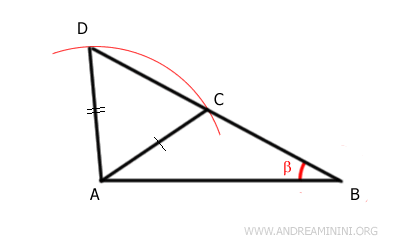
It is evident that the two triangles ABC and ABD are not congruent because they are not superimposable. Triangle ABD is larger than triangle ABC. However, both triangles have two congruent sides, AB ≅ AB and AC ≅ AD, and a congruent angle β. But the angle β is not included between the two congruent sides. In conclusion, two congruent sides and a non-included angle are not sufficient to declare the congruence of the triangles.
Illustrating the Postulate
The first triangle congruence criterion is treated as a postulate because it rests on Euclid’s foundational axioms.
As such, what follows isn’t a rigorous proof in the formal sense, since rigid motions are understood as intuitive geometric transformations.
Let’s take two triangles, ABC and A'B'C'
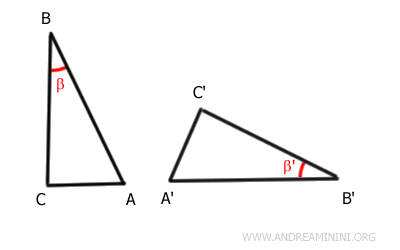
According to the hypothesis, the segments AB and A'B', as well as BC and B'C', are equal in length, and the included angles β and β' are congruent.
We now apply a rigid motion - a combination of rotation and translation - to align side AB with side A'B', ensuring that angle β also coincides with angle β'.
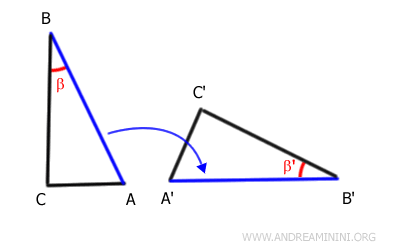
Since AB perfectly matches A'B', their endpoints must coincide as well.
Therefore, point A aligns with point A', and point B aligns with point B'.
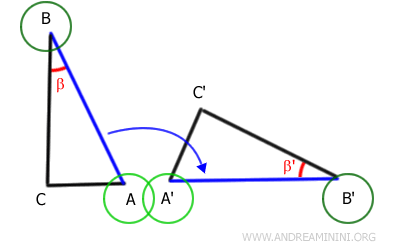
Because angles β and β' lie adjacent to these matched sides, they also overlap exactly. This confirms they have equal measure - that is, they are congruent.
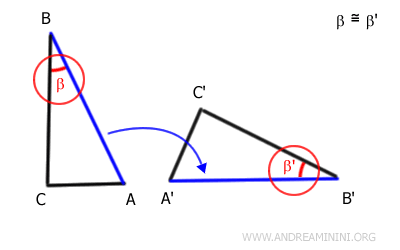
Consequently, with the included angle congruent and sides equal, segment BC must also fall precisely onto segment B'C'.
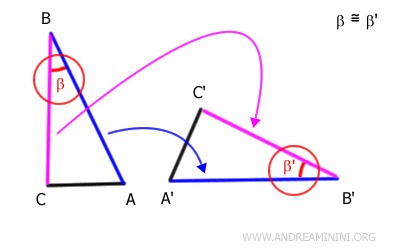
This means their endpoints align as well.
We already knew that point B coincides with point B', and now we see that point C coincides with point C'.
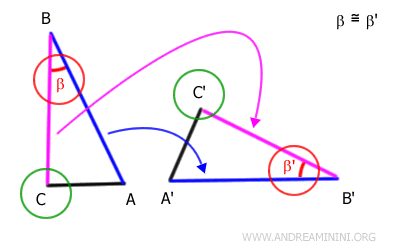
It follows that segment AC must also coincide with A'C', since both pairs of endpoints overlap.
In conclusion, all corresponding vertices of the two triangles match after the rigid transformation. This means that all sides and angles are congruent in corresponding order.
Hence, we can state that the two triangles are congruent.
And so on.
