Intersecting Lines
Two or more distinct lines are called intersecting lines if they cross at exactly one point.
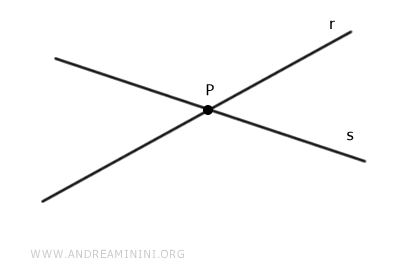
Two lines intersect when they share exactly one point.
This is because only one line can pass through two distinct points.
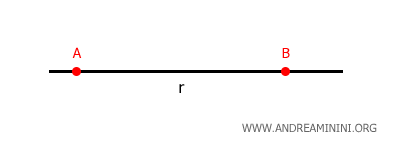
When two lines share more than one point, they are coincident lines.
Thus, two lines can only intersect if they have one point in common.
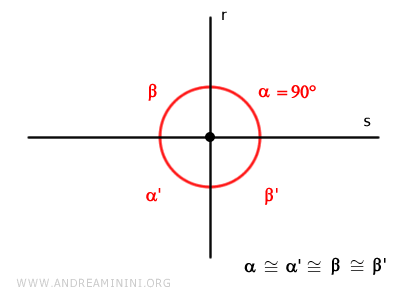
The intersection of two lines divides the Cartesian plane into four regions, with two pairs of congruent vertical angles.
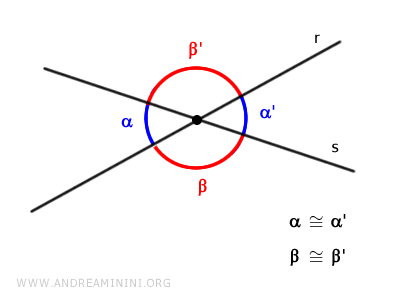
Depending on the size of the angles, intersecting lines can be classified as:
- Perpendicular Lines
When all four vertical angles are right angles (90°), the lines are perpendicular.
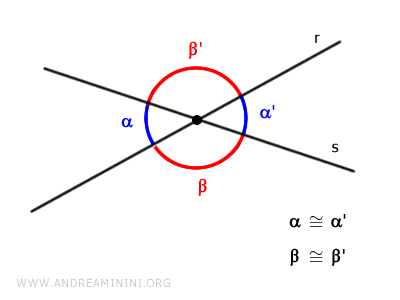
- Oblique Lines
When two intersecting lines are not perpendicular, they are called oblique lines.
How to Find the Intersection Point of Lines on the Plane
In analytic geometry, to find the intersection point of two lines on the Cartesian plane, you solve a system of two linear equations. $$ \begin{cases} ax+by+c=0 \\ \\ a'x+b'y+c'=0 \end{cases} $$ Each equation represents a line on the plane.
Solving the system of equations can yield three outcomes:
- The system has a unique solution. In this case, the system is consistent, and the solution consists of two values, x and y, which correspond to the coordinates (x;y) of the intersection point. This means the lines intersect at a specific point. This occurs when the coefficients "a" and "b" of the variables x and y are not proportional, indicating different slopes for the two lines. $$ \frac{a}{a'} \ne \frac{b}{b'} \Longleftrightarrow m \ne m' $$
- The system has no solution. In this case, the system is inconsistent. This means the lines do not intersect and are parallel and distinct. This occurs when the coefficients "a" and "b" of the variables x and y in the two equations are proportional, but the constant term "c" is not. $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$
- The system has infinite solutions. In this case, the system is indeterminate. This means the lines are coincident, sharing all points in common. This occurs when the ratios of the coefficients and the constant terms of the two equations are proportional. $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$
Using algebra, you can determine the intersection point of two lines, if it exists, and the nature of the lines: intersecting, parallel, or coincident.
Example
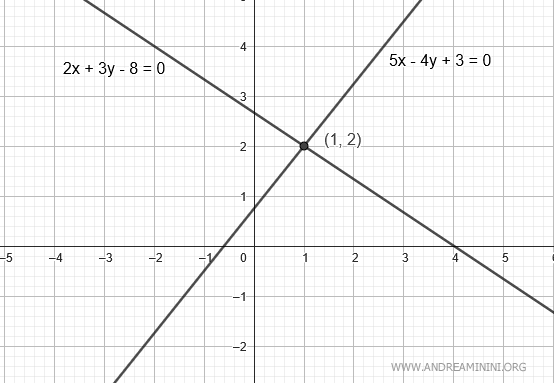
Consider two lines with the following implicit equations:
$$ r: \ 2x+3y-8=0 $$
$$ r': \ 5x-4y+3=0 $$
We need to determine if they intersect, are parallel, or are coincident.
To do this, calculate the ratio of the coefficients of the variables x and y.
$$ \frac{a}{a'} = \frac{2}{5} $$
$$ \frac{b}{b'} = \frac{3}{4} $$
Since the ratios are different,
$$ \frac{a}{a'} \ne \frac{b}{b'} $$
the lines intersect.
How to Calculate the Intersection Point of Intersecting Lines
To find the point where the two lines intersect, set up the two equations as a system.
$$ \begin{cases} 2x+3y-8=0 \\ \\ 5x-4y+3=0 \end{cases} $$
Then, solve the system of linear equations.
In this case, we use the substitution method to find the value of one variable from one equation. For example, x.
$$ \begin{cases} x=\frac{8-3y}{2} \\ \\ 5x-4y+3=0 \end{cases} $$
$$ \begin{cases} x=\frac{8}{2} - \frac{3y}{2} \\ \\ 5x-4y+3=0 \end{cases} $$
$$ \begin{cases} x=4 - \frac{3y}{2} \\ \\ 5x-4y+3=0 \end{cases} $$
Then, substitute x into the other equation.
$$ \begin{cases} x=4 - \frac{3y}{2} \\ \\ 5[ 4 - \frac{3y}{2} ]-4y+3=0 \end{cases} $$
$$ \begin{cases} x=4 - \frac{3y}{2} \\ \\ 20-\frac{15y}{2} -4y+3=0 \end{cases} $$
$$ \begin{cases} x=4 - \frac{3y}{2} \\ \\ 23 + (\frac{-15y-8y}{2} )=0 \end{cases} $$
$$ \begin{cases} x=4 - \frac{3y}{2} \\ \\ 23 - \frac{23y}{2}=0 \end{cases} $$
$$ \begin{cases} x=4 - \frac{3y}{2} \\ \\ \frac{23y}{2}=23 \end{cases} $$
$$ \begin{cases} x=4 - \frac{3y}{2} \\ \\ y=23 \cdot \frac{2}{23} \end{cases} $$
$$ \begin{cases} x=4 - \frac{3y}{2} \\ \\ y= 2 \end{cases} $$
Once we find y=2, substitute it into the first equation to find the value of x.
$$ \begin{cases} x=4 - \frac{3 \cdot 2}{2} \\ \\ y= 2 \end{cases} $$
$$ \begin{cases} x=4 - 3 \\ \\ y= 2 \end{cases} $$
$$ \begin{cases} x=1 \\ \\ y= 2 \end{cases} $$
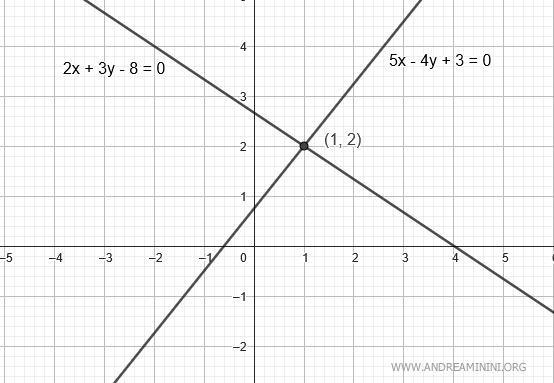
Therefore, the two lines intersect at the coordinates x=1 and y=2, which is the intersection point (x;y)=(1;2).
Observations
Some observations about intersecting lines:
- If two lines a and b intersect, then their respective parallel lines a' and b' also intersect.
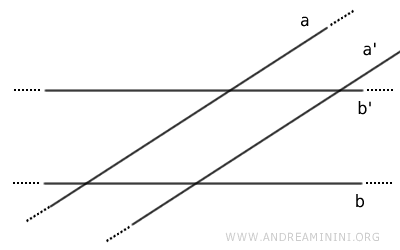
Proof. By contradiction, assume the opposite is true. Given two intersecting lines a and b, their respective parallel lines a' and b' are parallel to each other a' // b' $$ a \parallel a' $$ $$ b \parallel b' $$ $$ a' \parallel b' $$ However, if this were the case, by the transitive property, lines a and b would also be parallel $$ a' \parallel b' \ , \ b' \parallel b \Rightarrow a \parallel b $$ This contradicts the initial assumption that lines a and b are intersecting. Therefore, the statement is false. Its negation is true: if two lines a and b intersect, their respective parallel lines a' and b' also intersect.
And so on
