Perpendicular Line Theorem for Two Planes

If a line $ r $ is perpendicular to two planes $ \alpha $ and $ \beta $ at points $ P $ and $ Q $, respectively (where $ P $ and $ Q $ are distinct points on the line), then the two planes $ \alpha $ and $ \beta $ are parallel, i.e., $ \alpha \parallel \beta $.
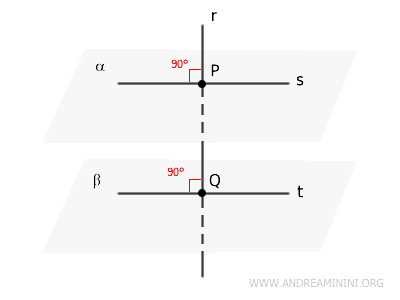
proof illustration

This theorem in solid geometry is a powerful tool for analyzing the relationships between lines and planes in three-dimensional space.

The Proof

Let $ r $ be a line that intersects the planes $ \alpha $ and $ \beta $ at points $ P $ and $ Q $, respectively.

By assumption, $ r $ is perpendicular to both $ \alpha $ and $ \beta $.

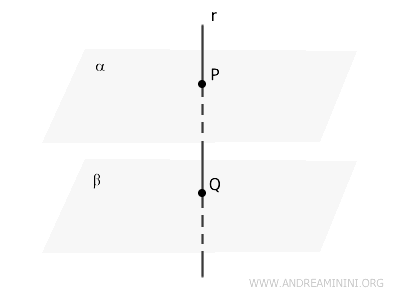
example of a line perpendicular to a plane

This means $ r $ forms a right angle with every line lying in $ \alpha $ that passes through $ P $, as well as with every line lying in $ \beta $ that passes through $ Q $.

Next, consider a line $ s $ in $ \alpha $ passing through $ P $, and a line $ t $ in $ \beta $ passing through $ Q $.

proof illustration

Since $ r $ is perpendicular to $ \alpha $, it must also be perpendicular to $ s $.

Similarly, $ r $ is perpendicular to $ t $.

Now, let’s assume for the sake of contradiction that $ \alpha $ and $ \beta $ are not parallel.

If $ \alpha $ and $ \beta $ were not parallel, they would intersect along a line $ u $. This would mean $ u $ belongs to both $ \alpha $ and $ \beta $.

Since $ r $ is perpendicular to all lines in $ \alpha $ passing through $ P $, it would also be perpendicular to $ u $ because $ u $ lies in $ \alpha $.

$$ u \subset \alpha $$

Likewise, because $ r $ is perpendicular to all lines in $ \beta $ passing through $ Q $, it would also be perpendicular to $ u $ since $ u $ lies in $ \beta $.

$$ u \subset \beta $$

However, it is impossible for a single line $ r $ to be perpendicular to the same line $ u $ at two distinct points $ P $ and $ Q $, as this would contradict the uniqueness of a perpendicular line at a given point.

Thus, the assumption that $ \alpha $ and $ \beta $ are not parallel is false.

Consequently, the two planes must be parallel.

Alternative Proof

Consider a line $ r $ that is perpendicular to the plane $ \alpha $ at point $ P $.

Since $ r $ is perpendicular to $ \alpha $ at $ P $, the direction vector of $ r $, denoted as $ \vec{v} $, is a normal vector (orthogonal) to the plane $ \alpha $.

This means $ \vec{v} $ is perpendicular to every vector in $ \alpha $.

Similarly, $ r $ is perpendicular to $ \beta $ at point $ Q $, so $ \vec{v} $ is also a normal vector to the plane $ \beta $.

Since $ \vec{v} $ serves as the normal vector for both $ \alpha $ and $ \beta $, the two planes share the same normal direction, which implies their normal vectors are parallel.

When two planes have parallel normal vectors, the planes themselves must be parallel. Therefore, $ \alpha $ and $ \beta $ are parallel.

And so the theorem is proved.