Three Perpendicular Lines Theorem

If two lines $ a $ and $ b $, perpendicular to a line $ r $, are drawn from a point $ P $ on $ r $, then $ r $ is perpendicular to any other line $ s $ that passes through $ P $ and lies in the plane $ \alpha $ formed by $ a $ and $ b $.
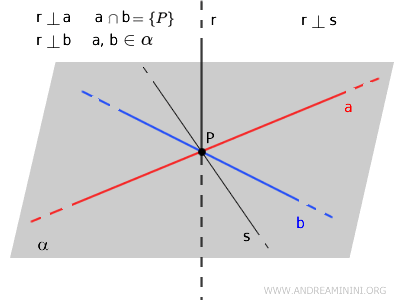
example

The three perpendicular lines theorem is particularly valuable in three-dimensional geometry for establishing orthogonality between lines and planes.

For example, it provides a straightforward way to verify if a line is perpendicular to another line or a plane by analyzing their relationships within the associated plane.

The Proof

Let’s start with a point $ P $ and a line $ r $.

Draw two lines $ a $ and $ b $, both perpendicular to $ r $, passing through $ P $.

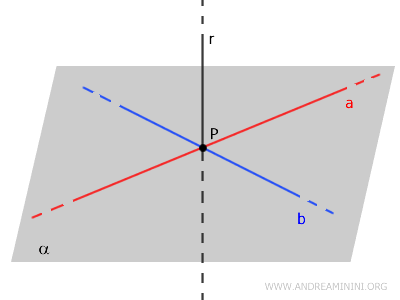
example

The lines $ a $ and $ b $ define the plane $ \alpha $, making them coplanar.

By construction, the lines $ a $ and $ b $ intersect at $ P $ and are both perpendicular to $ r $.

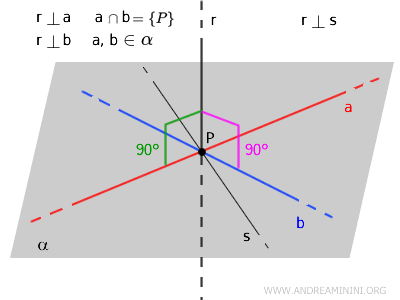
$$ a \cap b = \{ P \} $$

$$ a, b \in \alpha $$

$$ a , b \perp r $$

Thus, $ r $ is perpendicular to the plane $ \alpha $, and their intersection is limited to point $ P $.

$$ r \cap \alpha = \{ P \} $$

example

Now, choose two points $ Q $ and $ R $ on $ r $, equidistant from $ P $ on opposite sides of the plane $ \alpha $.

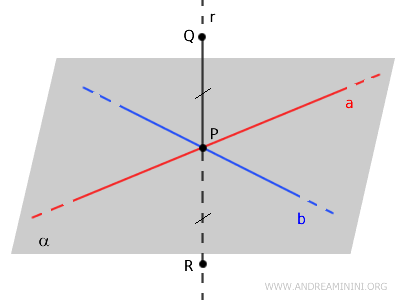
example

Since $ Q $ and $ R $ are equidistant from $ P $, the segments $ PQ $ and $ PR $ are congruent:

$$ PQ \cong PR $$

Next, draw a line $ s $ within the plane $ \alpha $.

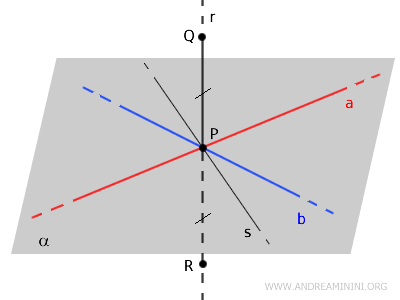
example

Select two points $ A $ and $ B $ on $ a $ and $ b $, respectively, and connect them with a segment $ AB $ that intersects $ s $ at $ T $.

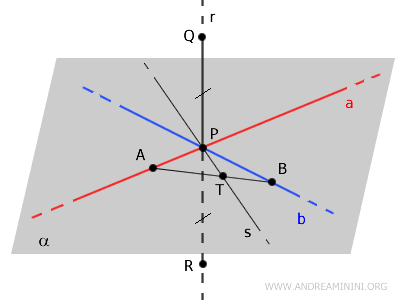
proof

Draw segments $ AQ, TQ, BQ $ and $ AR, TR, BR $, forming several triangles.

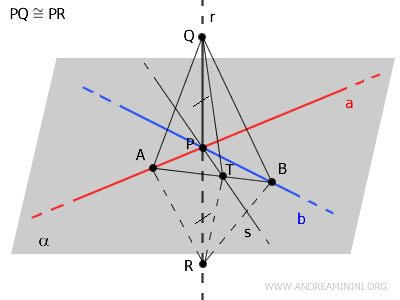
example

In $ \triangle AQR $, the segment $ AP $ acts as both the altitude and the median relative to the base $ QR $, since $ PQ \cong PR $.

This proves that $ \triangle AQR $ is an isosceles triangle, so $ AQ \cong AR $.

$$ PQ \cong PR $$

Similarly, $ \triangle BQR $ is isosceles because $ PB $ serves as both the altitude and the median relative to $ QR $.

Thus, $ BQ \cong BR $.

$$ BQ \cong BR $$

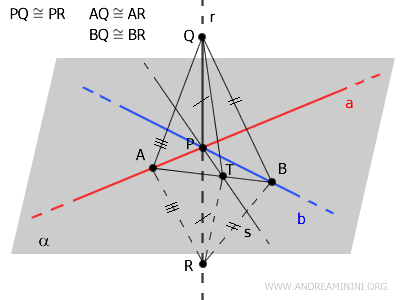
example

Now, consider triangles $ \triangle ABQ $ and $ \triangle ABR $.

According to the third congruence criterion, $ \triangle ABQ \cong \triangle ABR $, as they share the side $ AB $ and have two pairs of congruent sides: $ AQ \cong AR $ and $ BQ \cong BR $.

$$ ABQ \cong ABR $$

Since these triangles are congruent, their corresponding angles are equal.

Specifically, $ \angle ABQ $ and $ \angle ABR $ are congruent.

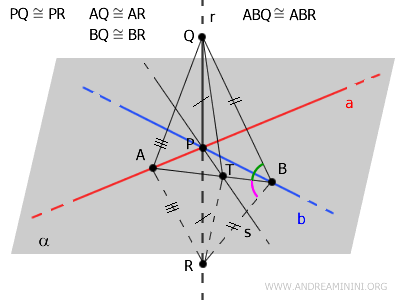
example

In triangles $ \triangle TBQ $ and $ \triangle TBR $, the side $ TB $ is shared, $ BQ \cong BR $, and the angles $ \angle ABQ $ and $ \angle ABR $ are congruent.

By the first congruence criterion, $ \triangle TBQ \cong \triangle TBR $.

$$ TBQ \cong TBR $$

Since $ \triangle TBQ $ and $ \triangle TBR $ are congruent, all their sides are equal.

In particular, $ TQ \cong TR $.

$$ TQ \cong TR $$

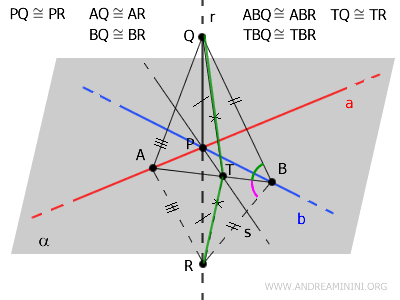
example

Knowing $ TQ \cong TR $, we can conclude that $ \triangle TQR $ is isosceles.

Thus, $ PT $ serves as both the altitude and the median of $ \triangle TQR $.

This establishes that $ PT $ is perpendicular to the base $ QR $, forming a $ 90^\circ $ angle.

$$ PT \perp QR $$

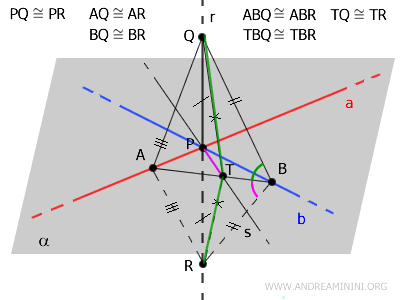
example

Finally, since $ QR $ lies on line $ r $ and $ PT $ lies on line $ s $, we conclude that lines $ r $ and $ s $ are perpendicular.

$$ r \perp s $$

The same reasoning applies to any line $ s $ within the plane $ \alpha $.

example

With this, the theorem is proven.

And so forth.